
- •В.А.Ганов учебно-методический комплекс
- •280700.62 «Техносферная безопасность»
- •Оглавление
- •Пояснительная записка
- •1). Цели и задачи дисциплины, ее место в учебном процессе
- •2). Общие пояснения
- •2.Основные требования государственного образовательного стандарта
- •3.2. Содержание учебной дисциплины
- •4. Разделы учебной дисциплины, виды учебной деятельности и формы контроля
- •5. Самостоятельная работа студента
- •5.1. График самостоятельной работы студента
- •6. Оценочные средства для контроля успеваемости ирезультатов освоения учебной дисциплины
- •7.Литература
- •2.5.1. Основная литература
- •7. Материально-техническое обеспечение учебной дисциплины
- •2.6.1. Требования к аудиториям (помещениям, местам) для проведения занятий:
- •7.2. Требования к оборудованию рабочих мест преподавателя и обучающихся:
- •8.Тематический план (распределение часов курса по темам и видам работ):
- •1 Семестр
- •2 Семестр
- •3 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •1 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •2 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •3 Семестр
- •10.Контрольные задания и тесты
- •Вариант 2.
- •13.Какой из следующих определителей не равен нулю?
- •Вариант 2
- •Вариант 19
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 27
- •Утверждаю: Зав. Кафедрой_________________
- •11.1. Вопросы к экзамену по дисциплине «Высшая математика»,
- •8.1.2.Экзаменационные билеты по высшей математике
- •11.2.Экзаменационные вопросы
- •11.2.Экзаменационные билеты (2-й семестр)
- •8.3.1.Экзаменационные вопросы
- •8.3.2.Экзаменационные билеты по высшей математике 3-й семестр
- •Учебные пособия
- •Оглавление
- •Глава 1. Элементы линейной алгебры
- •§1. Числовые матрицы и определители
- •Основные свойства матриц
- •Основные свойства определителей
- •§2. Обратная матрица
- •§3. Системы линейных уравнений
- •2) Если определитель а равен нулю и хотя бы один из I отличен от нуля, то система (5) не имеет решений;
- •3) Если определитель а и все вспомогательные определители I равны нулю, то система (5) имеет бесконечное множество решений.
- •1) Если в (7) нет противоречий и число уравнений равно числу неизвестных, то система (3) имеет единственное решение;
- •2) Если (7) содержит противоречие, то система (3) не имеет решений;
- •3) Если в (7) нет противоречий, но число уравнений меньше числа неизвестных, то система (3) имеет бесконечное множество решений.
- •§4. Ранг матрицы и неопределенные системы
- •Упражнения 1
- •Глава 2. Аналитическая геометрия
- •§1. Декартова система координат
- •§2. Уравнение прямой линии на плоскости
- •§3. Кривые линий второго порядка
- •§4. Декартовы координаты и векторы в пространстве
- •2). Координаты точки деления отрезка в заданном отношении вычисляют по формулам:
- •§5. Скалярное произведение векторов
- •Свойства скалярного произведения
- •§6. Векторное и смешанное произведения
- •Свойства векторного произведения
- •§7. Плоскость и прямая линия в пространстве
- •2).Условие параллельности плоскостей:
- •Основное правило 1.
- •2).Условие параллельности прямых:
- •Основное правило 2.
- •Упражнения 2
- •Глава 3. Поверхности второго порядка
- •§1.Сферические, цилиндрические и конические поверхности
- •Частные случаи.
- •§2.Стандартные поверхности 2-го порядка
- •§3. Поверхности вращения
- •Упражнения 3
- •Глава 4. Комплексные числа
- •§1. Алгебраическая форма комплексного числа
- •§2. Тригонометрическая форма комплексного числа
- •Упражнения 4
- •Глава 5. Разложение рациональных дробей
- •Правило разложения правильной вещественной дроби на простейшие дроби.
- •Глава 6. Введение в математический анализ
- •§1. Числовые функции
- •§2. Простейшие функции
- •Основные свойства степеней
- •Основные свойства логарифмов
- •6. Тригонометрические функции.
- •Обратные тригонометрические функции.
- •§3. Бесконечные величины и предел функции
- •Свойства пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Теперь исходный предел равен: §4. Непрерывные функции
- •3) F(X) принимает на [a; b] все промежуточные значения между своими наименьшим и наибольшим значениями.
- •Упражнения 4
- •Упражнения 5
- •Библиографический список
- •Часть 2
- •Глава 1. Дифференциальное исчисление………………………………………………….5
- •§1. Производная функции одной переменной
- •Правила дифференцирования
- •§2. Задачи, приводящие к понятию производной функци
- •§4. Основные теоремы о дифференцируемых функциях
- •§5. Исследование функций на монотонность и экстремум
- •Задачи на экстремум.
- •§6. Вогнутость и точки перегиба
- •Определение 6.Точки, в которых график функции меняет направление вогнутости называютсяточками перегиба.
- •Упражнения 1
- •Ответы к упражнениям 1
- •Глава 2. Интегральное исчисление
- •§1. Неопределенный интеграл
- •Правила интегрирования
- •Основные свойства неопределенных интегралов
- •§2. Методы интегрирования
- •3.Интегрирования по частям. Пусть u и V - дифференцируемые функции от х, тогда верно равенство
- •5. Интегрирование некоторых тригонометрических функций.
- •§3. Определенный интеграл
- •Свойства определенного интеграла
- •§4.Приложения определенных интегралов
- •1.Вычисление площади плоской фигуры, ограниченной линиями
- •§5. Несобственные интегралы
- •Упражнения 2
- •Ответы к упражнениям 2
- •Глава 3. Функции нескольких переменных
- •§1. Евклидово n-мерное пространство
- •§2. Экстремумы функций двух переменных
- •§3. Метод наименьших квадратов
- •Упражнения 3
- •Глава 4. Функции комплексного переменного
- •§1. Определение и геометрическое и изображение
- •Предел и непрерывность функции комплексного переменного
- •§2. Элементарные функции комплексного переменного
- •§3. Дифференцирование
- •Другие свойства
- •Геометрический смысл производной
- •Глава 5. Дифференциальные уравнения
- •§1. Дифференциальные уравнения 1-го порядка
- •Теорема о существовании решения задачи Коши
- •Методы интегрирования дифференциальных уравнений
- •§2. Дифференциальные уравнения 2-го порядка
- •Теорема существования решения задачи Коши
- •Методы понижения порядка.
- •§3. Линейные уравнения 2-го порядка
- •§4. Линейные уравнения с постоянными коэффициентами
- •Упражнения 5
- •Глава 8.Элементы теории вероятностей
- •§1.Определение вероятности и ее свойства
- •Свойства вероятности
- •§2. Повторные независимые испытания
- •§3. Случайные величины
- •Основные свойства функции распределения f(X)
- •Основные свойства плотности распределения f(X)
- •Свойства математического ожидания
- •Свойства дисперсии
- •Основные виды распределений
- •§4. Закон больших чисел
- •Приложение 1.Элементы комбинаторики Основные правила комбинаторики
- •Простейшие соединения
- •Упражнения 7
- •Упражнение 8
- •Библиографический список
- •Приложение 2. Математико-статистические таблицы
- •Глава 8. Введение в математическую статистику
- •§1. Выборочный метод
- •Основные виды распределений
- •Упражнение 8
Правило разложения правильной вещественной дроби на простейшие дроби.
Согласно
теореме 3 из главы 3, полином
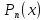 с вещественными
коэффициентами разлагается на произведение
полиномов вида
с вещественными
коэффициентами разлагается на произведение
полиномов вида
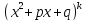 и
и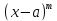 ,
гдеa, p, q
– вещественные числа. Тогда правильная
вещественная дробь
,
гдеa, p, q
– вещественные числа. Тогда правильная
вещественная дробь
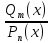 будет разлагаться в сумму простейших
вещественных дробей вид
будет разлагаться в сумму простейших
вещественных дробей вид
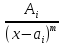 и
и
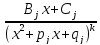 по следующему правилу. Сначала описываются
правила выбора простейших дробей с
неопределенными коэффициентами
по следующему правилу. Сначала описываются
правила выбора простейших дробей с
неопределенными коэффициентами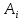
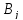 ,
,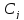 .
.
Знаменатель
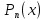 разлагают на простейшие вещественны
множители.
разлагают на простейшие вещественны
множители.По множителям составляют простейшие дроби с неопределенными коэффициентами по следующим правилам.
3.Пусть
множитель
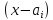 входит в разложение
входит в разложение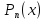 один раз, тогда в формулу разложения
включается одна простейшая дробь
один раз, тогда в формулу разложения
включается одна простейшая дробь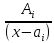 ,
где
,
где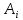 -неопределенный
коэффициент.
-неопределенный
коэффициент.
2.Пусть
множитель
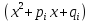 входит в разложение
входит в разложение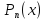 один раз, тогда в формулу разложения
включается одна простейшая дробь
один раз, тогда в формулу разложения
включается одна простейшая дробь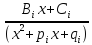 ,
где
,
где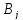 ,
,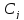 - неопределенные коэффициенты.
- неопределенные коэффициенты.
3.
Пусть множитель
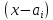 входит в разложение
входит в разложение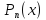 m
раз, тогда в формулу разложения включаются
простейшие дроби
m
раз, тогда в формулу разложения включаются
простейшие дроби
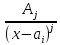 ,j=1,…,m.
,j=1,…,m.
4.Пусть
множитель
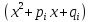 входит в разложение
входит в разложение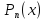 m
раз, тогда в формулу разложения включаются
простейшие дроби
m
раз, тогда в формулу разложения включаются
простейшие дроби
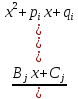 ,
j=1,…,m.
,
j=1,…,m.
Формула
разложения дроби на простейшие – это
сумма выбранных простейших дробей с
неопределенными коэффициентами, которая
приравнивается к исходной дроби
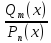 .
.
5. Обе части формулы приводят к общему знаменателю и приравнивают числители.
6.В
полученном тождестве приравнивают
коэффициенты при одинаковых степенях
x.Получается
систама относительно неопределенных
коэффициентов
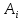
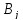 ,
,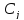 .
.
7. Эта система решается, и найденные коэффициенты подставляют в формулу разложения
Пример
4. Разложить
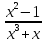 .
на простейшие дроби.
.
на простейшие дроби.
Решение. Разлагается знаменатель дроби на простейшие множители x(x2+1). Формула разложения данной дроби имеет вид
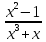 =
=
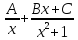 .
.
Отсюда
следует тождество: Ax2+A+Bx2+Cx
= x21;
приравниваются коэффициенты при
одинаковых степенях x,
получается система:A
+ B=1, C = 0, A = 1.
Получено решение A
= -1,
B = 2, C
= 0. Тогда
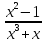 =
=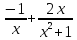 .
.
Глава 6. Введение в математический анализ
§1. Числовые функции
Рассматривается некоторый переменный процесс (например: физический, химический или социальный), и в нем наблюдаются некоторые величины, значениями которых являются числа (например: вес, температура, расстояние, стоимость, прибыль и т.п.). Величины разделяются на постоянные и переменные: постоянные величины принимают одно и то же значение в течение всего процесса, переменные величины могут принимать различные значения. Постоянные величины обозначаются первыми буквами латинского алфавита: а, b, c (возможно с некоторыми дополнительными индексами). Постоянные величины такженазываются константами. Переменные величины обозначаются последними буквами: х, y, z, t (возможно с индексами), и называются переменными. Конкретные значения переменных х или y обозначаются теми же буквами с дополнительным числовым индексом, например, х0 или y1.
В наблюдаемом процессе между величинами могут быть разного рода зависимости, среди которых центральное место занимает функциональная зависимость.
Определение 1. Пусть каждому значению переменной х соответствует определенное значение переменной у, тогда говорят, что у функционально зависит от х, или у есть функция от х. При этом х называется независимой переменной или аргументом, и у зависимая переменная или функция. Закон соответствия между значениями переменных х и у обозначается буквами f, g, и используются записи вида: у = f(x), у = g(x) или, просто, f(x), g(x).
Если значению аргумента хо соответствует значение уо функции f(x), то говорят, что функция f(x) определена в точке хо и уо ее значение в этой точке, обозначение: yо= f(xо). Множество всех значений х, в которых функция f(x) определена, называется областью определения f(x), обозначение: Df .
Множество всевозможных значений функции f(x) называется областью значений f(x), обозначение: Еf .
Если функция f(x) определена о всех точках, то она называется всюду определенной функцией; в противном случае, f(x) не всюду определенная или частичная функция. Рассматриваются следующие способы задания функций.
1. Аналитический способ. Это означает задание функции некоторой формулой, например:
у = (х 3)3, у = 5х /(x2+3x+5), у = log2 (4x + 2), у = ех.
Это наиболее полный и универсальный способ задания функции.
2.Табличный способ. Все значения аргумента x (или наиболее употребительные из них) и соотвествующие им значения функции f(x) выписываются в виде таблицы. Например:
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
|
f(x) |
0,001 |
0,036 |
0,125 |
0,45 |
0,304 |
0,084 |
Этот способ позволяет быстро находить нужные значения функции.
3. Графический способ. В этом случае задание функции (или её части) осуществляется с помощью графика. Графиком функции у = f(x) в декартовой системе координат называется множество всех точек М(х; у), координаты которых удовлетворяют равенству: у = f(x). Преимущество этого способа наглядность.
Определение 2. Функция у = f(x) называется чётной, если ее область определения симметрична относительно нуля и для всех допустимых знпчений аргумента х выполняется равенство:
f(x) f(x).
Точки М1(х; у) и М2(х; у) являются симметричными относительно оси ОY. Тогда из данного определения следует, что в случае четной функции у = f(x) для таких точек одновременно выполняются (или не выполняются) равенства: у = f(x) и у = f(x), т.е. график четной функции состоит из точек, симметричных относительно ОY. Другими словами, этот график симметричен относительно оси ОУ.
Определение 3. Функция у = f(x) называется нечётной, если ее область определения симметрична относительно нуля и для всех допустимых знпчений аргумента x выполняется тождество:
f(x) f(x).
Точки
М1(х;
у)
и М2(х;
у)
являются симметричными относительно
начала координат О.
Из данного определения следует, что в
случае нечетной функции у
= f(x)
для таких точек одновременно выполняются
(или не выполняются) равенства: у
= f(x)
и у
= f(x),
т.е. график нечетной функции состоит из
точек, симметричных относительно О.
Другими словами, этот график симметричен
относительно начала
координат О.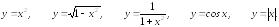
Примеры 1. 1).Четные функции:
Действительно,
эти функции удовлетворяют тождеству
из определения 2: (х)2
= х2;
 и т. д.
и т. д.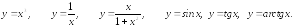
2). Нечетные функции:
Действительно, эти функции удовлетворяют тождеству из определения 3:
(х)3
= х3;
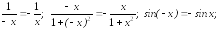 и т. д.
и т. д.
Определение 4. Функция f(x) называется возрастающей на интервале (a; b), если на этом интервале большему значению аргумента соответствует большее значение функции, т. е. для всех х1, х2(a; b) выполняется соотношение:
x1 < x2 f(x1) < f(x2).
Функция f(x) называется убывающей на интервале (a; b), если на этом интервале большему значению аргумента соответствует меньшее значение функции, т. е. для всех х1, х2(a; b) выполняется соотношение:
x1 < x2 f(x1) > f(x2).
Примеры 2. 1). Возрастающие функции на (; +):

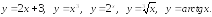
2). Убывающие функции на (; +):
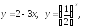
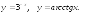
3). Функции, убывающие на (; 0) и возрастающие на (0; +):
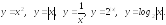
Определение 5. Функция f(x) называется ограниченной на (a; b), если существует число М такое, что все значения функции f(x) на (a; b) не превосходят М по абсолютной величине, т. е. для всех х(a; b) выполняется неравенство: |f(x)| М.
Если же f(x) принимает сколь угодно большие значения на (a; b), то она называется неограниченной функцией, т.е. для любого числа М найдется значение х(a; b) такое, что |f(x)| > М.
Пример 3. 1). Ограниченные функции:
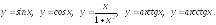
Здесь
значения первых трех функций заключены
в сегменте [1;
+1], значения четвертой и пятой функций
заключены в интервалах
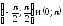 ,
соответственно (см. ниже рис.8).
,
соответственно (см. ниже рис.8).
2). Неограниченные функции:
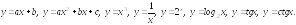
Эти функции могут принимать сколь угодно большие значения ( см. ниже рис.1-3,7).
Над функциями можно производить такие же операции, как над числами, согласно следующим определениям.
Суммой функций f(x) и g(x) называется функция (f + g)(x), значениями которой являются суммы соответствующих значений этих функций:
(f + g)(x) = f(x) + g(x).
Произведением функций f(x) и g(x) называется функция (fg)(x), значениями которой являются произведения соответствующих значений этих функций:
(fg)(x) = f(x)g(x).
Аналогично
определяются другие математические
операции над функциями, например: (f
g)(x)
= f(x)
g(x);
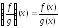 .
.
Определение 6. Суперпозицией функций y = f(x) и y = g(x) называется функция (обозначаемая через fg), значениями которой являются значения функции f(x) от соответствующих значений функции g(x): (fg)(x) = f(g(x)). Говорят также, что fg – результат подстановки функции g(x) в функцию f(x).
Пример 4. а) пусть f(x) = x3 и g(x) = 1+ х2 , тогда
(fg)(x) = (1 + х2)3 и (gf)(x) = 1 + (x3)2 = 1 + x6;
б)
пусть f(x)
= и g(x)
= lоg2х,
тогда
и g(x)
= lоg2х,
тогда
(fg)(x)
=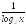 и (gf)(x)
= lоg2(
и (gf)(x)
= lоg2( )
=lоg2х.
)
=lоg2х.
