Основные виды распределений

Случайная величина Х распределена равномерно на промежутке [a; b], если ее плотность распределения 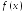имеет вид:

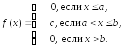
Из второго свойства следует, что. Тогда математическое ожидание находится следующим образом.

= .

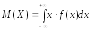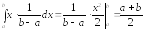Дисперсия находится по формуле (63).

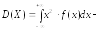
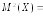
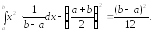
Пример 17. Случайная величина Х имеет равномерное распределение

на промежутке [1; 2]. Найти плотность распределения Z = 3X+2. Решение. Плотность распределения 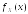случайной величины Х имеет указанный выше вид са = 1, b = 2 и с = 1. Делается замена z = 3x+2 и доказы-

вается, что плотность случайной величины Z будет равна:

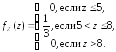
Биноминальное распределение случайной величины Х  это распределение, при котором Х принимает целые значения от 0 до n, и для каждого m вероятность того, что Х= m вычисляется по формуле Бернулли (58):

Р(Х = m) = С_n^mp^mq^nm. Для такой случайной величины Х числовые характеристики вычисляются по формулам:

(64)

Нормальный закон распределения случайной величины Х  это распределение, при котором плотность распределения Х имеет вид

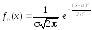или 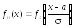, гдеа и   параметры,  3,14, е  2,72, f_л  функция Лапласа (см. §2).

Смысл указанных параметров следующий: а  математическое ожидание, ²  дисперсия и   среднее квадратическое отклонение Х, т. е. М(Х) = а; D(Х) =²; (Х) = .

Вероятность того, что Х принимает значения в промежутке от  до  равна

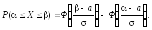(65)

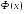
где  функция Лапласа (см. §2). В частности, вероятность того, что Х отклоняется от М(Х) = а не более, чем на , находится по формуле

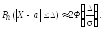(66)

Пример 18. Вероятность того, что при перевозке повредится упаковка изделия, равна 0,1. Найти закон распределения числа изделий с поврежденной упаковкой при перевозке четырех изделий; вычислить математическое ожидание и дисперсию и проверить (64).

Решение. Пусть Х число изделий с поврежденной упаковкой. Для каждого изделия вероятность повредить упаковку одинаковая, поэтому вероятность события Х= m равна Р_n(m), где n = 4, m = 0, 1, 2, 3 или 4, p = 0,1, q = 0,9. Следовательно, Х имеет биномиальное распределение. Тогда Р(Х=0) = С₄^0,1⁰0,9⁴ = 0,6562; Р(Х = 1) = С₄^0,1¹0,9³ = 0,2916; Р(Х = 2) = С_^0,1²0,9² = 0,0486; Р(Х = 3) = С₄^0,1³0,9 = 0,0036; Р(Х = 4) = С_^0,1⁴ 0,9⁰ = 0,0001. Теперь, закон распределения Х имеет вид:

Х	0	1	2	3	4
Р	0,6561	0,2916	0,0486	0,0036	0,0001

По формуле (6), М(Х) = 00,6561 + 10,2916 + 2 0,0486 + 30,0036 +

4 0,0001 = 0,4. Дисперсия D(Х) находится по формуле (63). Сначала находится М(Х^) = 0^0,6561 + 1^0,2916 + 2^0,0486 +3^0,0036 + 4^0,0001= 0,52. Тогда D(Х) = 0,52  0,4^ = 0,36. Теперь, проверяются формулы (64): М(Х) = 40,1 = 0,4; D(Х) = 40,1 0,9 = 0,36 верно.

Пример 19. Математическое ожидание нормально распределенной случайной величины Х равно 4, среднее квадратическое отклонение равно 2. Написать плотность распределения Х.

Решение. Параметры а и совпадают математическим ожиданием и средним квадратическим отклонением, поэтому вместо них в формулу плотности нормального закона подставляются числа 4 и 2: .

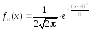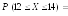
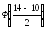
Пример 20. Случайная величина Х распределена по нормальному закону с М(Х) =10 и D(Х) = 4. Найти вероятность того, что Х принимает значения от 12 до 14. Решение. Применяется формула (65): 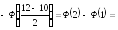Ф(4/2)  Ф(2/2) = 0,4772 0,3413 = 0,1359.

Пример 21. Производится взвешивание некоторого вещества без систематических ошибок. Ошибки взвешивания подчинены нормальному закону распределения с 10 г. Найти вероятность того, что взвешивание произведено с ошибкой не более чем 15 г по абсолютной величине.

Решение. Пусть Х - ошибка взвешивания, и Х распределена по нормальному закону, тогда применяется формула (66), при этом  = 10 и  = 15. Так как взвешивание производится без систематических ошибок, то М(Х)= 0, получается: Р(Х0  15) = 2Ф(15/10) = 2Ф(1,5) = 0,8664.

Пример 22. Случайная величина Х распределена по нормальному закону с М(Х) = 10 и (Х) = 5. Найти интервал, симметричный относительно М(Х) , в который попадает Х с вероятностью 0,9973.

Решение. Симметричный относительно М(Х) интервал имеет вид

(М(Х)  ; М(Х) +), где   некоторое число. Требуется найти  такое, чтобы вероятность события (М(Х)  Х  М(Х) + ) была равна 0.9973. Это событие записывается в виде ХМ(Х) , и тогда, по формуле (66), получается уравнение Ф() = 0,4982. По таблице 2 Ф(3) = 0,4982, следовательно:  = 3 и  = 3 = 35 = 15. Искомый интервал равен (5; 25).

Пример 7. Вероятность рождения мальчика равна 0,51. Найти:

а) вероятность того, что среди 100 новорожденных окажется 40 мальчиков.

б) вероятность того, что среди 70 новорожденных мальчиков появится не менее 51 и не более 65.

Решение:

а) Так как число испытаний (100) велико, то в этом случае удобнее использовать локальную теорему Муавра-Лапласа. Согласно этой теореме вероятность того, что в n независимых испытаниях событие произойдет m раз равна:

,

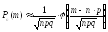Где значения функции φ(х) находят по специальной таблице. Заметим, что φ(х) – четная функция, т.е. φ(-х)= φ(х).

Тогда, подставляя n=100, р=0,51, q=1-0,51=0,49, m=40 в данную формулу, получим:

б) Вероятность Р_n(k_1, k₂) того, что в результате n независимых испытаний событие появится не менее k₁ и не более k₂ раз, вычисляется по интегральной теореме Муавра-Лапласа: 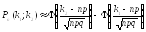, где Ф – функция Лапласа, ее значения находят по специальной таблице, причем Ф(-х)=-Ф(х) и для х≥5 полагают Ф(х)=0,5.

Тогда, полагая n=70, k₁=51, k₂=65, р=0,51, q=0,49, получаем:

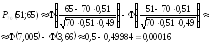
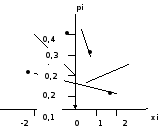
Пример 8. Дискретная случайная величина Х задана законом распределения:

Х	-2	0	1	2
р	0,2	0,4	0,3	0,1

а) построить многоугольник распределения и найти функцию распределения F(х);

б) найти М(х), D(х), σ(х).

Решение: Многоугольник распределения – это фигура, полученная путем соединения отрезками прямых точек с координатами (х_i, р_i).

Функция распределения F(х) определяет вероятность того, что Х в результате испытания примет значение, меньше чем х, т.е.

.

При х≤-2 значений Х, меньших -2 на существует, поэтому F(х)=0.

При -2<х≤0 есть только одно значение Х, меньшее 0, поэтому:

.

При 0<х≤1, аналогично получаем:

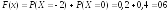
При 1<х≤2, получаем:

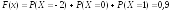
При х>2 все значения Х будут меньше х, поэтому F(х)=1.

Таким образом,

б) Для дискретных случайных величин числовые характеристики определяются по формулам:;;.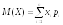

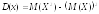Тогда М(Х)=-2·0,2+0·0,4+1·0,3+2·0,1=0,1.

Составим ряд распределения для Х²:

Х2	0	1	4
р	0,4	0,3	0,1+0,2

Тогда М (Х²)= 0·0,4+1·0,3+4·0,3=1,5.

Значит D(Х)=1,5-0,1²=1,49.

Тогда, .

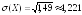Пример 9. Задана плотность распределения f(х) непрерывной случайной величины Х:

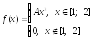
а) Найти А и функцию распределения F(х).

б) Найти М(х), D(х), σ(х).

Решение:

а) Для вычисления А используем свойство плотности f(х):

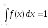, в частности, если все возможные значения случайной величины принадлежат интервалу (а,b), то .

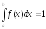Значит, 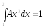, откуда,

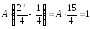, или .

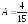Функция распределения F(х) и плотность f(х) связаны следующим соотношением:

.

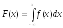1^й случай х<1. Тогда f(х)=0, значит и F(х)=0.

2^й случай 1≤х≤2. Тогда получаем:

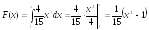
3^й случай х>2. Тогда: .

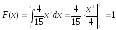Получили:

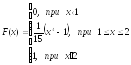
б) Для непрерывных случайных величин числовые характеристики находят по формулам: ;;.

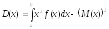Значит, ,

,

.
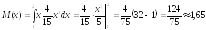
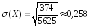