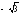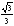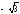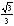- •В.А.Ганов учебно-методический комплекс
- •280700.62 «Техносферная безопасность»
- •Оглавление
- •Пояснительная записка
- •1). Цели и задачи дисциплины, ее место в учебном процессе
- •2). Общие пояснения
- •2.Основные требования государственного образовательного стандарта
- •3.2. Содержание учебной дисциплины
- •4. Разделы учебной дисциплины, виды учебной деятельности и формы контроля
- •5. Самостоятельная работа студента
- •5.1. График самостоятельной работы студента
- •6. Оценочные средства для контроля успеваемости ирезультатов освоения учебной дисциплины
- •7.Литература
- •2.5.1. Основная литература
- •7. Материально-техническое обеспечение учебной дисциплины
- •2.6.1. Требования к аудиториям (помещениям, местам) для проведения занятий:
- •7.2. Требования к оборудованию рабочих мест преподавателя и обучающихся:
- •8.Тематический план (распределение часов курса по темам и видам работ):
- •1 Семестр
- •2 Семестр
- •3 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •1 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •2 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •3 Семестр
- •10.Контрольные задания и тесты
- •Вариант 2.
- •13.Какой из следующих определителей не равен нулю?
- •Вариант 2
- •Вариант 19
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 27
- •Утверждаю: Зав. Кафедрой_________________
- •11.1. Вопросы к экзамену по дисциплине «Высшая математика»,
- •8.1.2.Экзаменационные билеты по высшей математике
- •11.2.Экзаменационные вопросы
- •11.2.Экзаменационные билеты (2-й семестр)
- •8.3.1.Экзаменационные вопросы
- •8.3.2.Экзаменационные билеты по высшей математике 3-й семестр
- •Учебные пособия
- •Оглавление
- •Глава 1. Элементы линейной алгебры
- •§1. Числовые матрицы и определители
- •Основные свойства матриц
- •Основные свойства определителей
- •§2. Обратная матрица
- •§3. Системы линейных уравнений
- •2) Если определитель а равен нулю и хотя бы один из I отличен от нуля, то система (5) не имеет решений;
- •3) Если определитель а и все вспомогательные определители I равны нулю, то система (5) имеет бесконечное множество решений.
- •1) Если в (7) нет противоречий и число уравнений равно числу неизвестных, то система (3) имеет единственное решение;
- •2) Если (7) содержит противоречие, то система (3) не имеет решений;
- •3) Если в (7) нет противоречий, но число уравнений меньше числа неизвестных, то система (3) имеет бесконечное множество решений.
- •§4. Ранг матрицы и неопределенные системы
- •Упражнения 1
- •Глава 2. Аналитическая геометрия
- •§1. Декартова система координат
- •§2. Уравнение прямой линии на плоскости
- •§3. Кривые линий второго порядка
- •§4. Декартовы координаты и векторы в пространстве
- •2). Координаты точки деления отрезка в заданном отношении вычисляют по формулам:
- •§5. Скалярное произведение векторов
- •Свойства скалярного произведения
- •§6. Векторное и смешанное произведения
- •Свойства векторного произведения
- •§7. Плоскость и прямая линия в пространстве
- •2).Условие параллельности плоскостей:
- •Основное правило 1.
- •2).Условие параллельности прямых:
- •Основное правило 2.
- •Упражнения 2
- •Глава 3. Поверхности второго порядка
- •§1.Сферические, цилиндрические и конические поверхности
- •Частные случаи.
- •§2.Стандартные поверхности 2-го порядка
- •§3. Поверхности вращения
- •Упражнения 3
- •Глава 4. Комплексные числа
- •§1. Алгебраическая форма комплексного числа
- •§2. Тригонометрическая форма комплексного числа
- •Упражнения 4
- •Глава 5. Разложение рациональных дробей
- •Правило разложения правильной вещественной дроби на простейшие дроби.
- •Глава 6. Введение в математический анализ
- •§1. Числовые функции
- •§2. Простейшие функции
- •Основные свойства степеней
- •Основные свойства логарифмов
- •6. Тригонометрические функции.
- •Обратные тригонометрические функции.
- •§3. Бесконечные величины и предел функции
- •Свойства пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Теперь исходный предел равен: §4. Непрерывные функции
- •3) F(X) принимает на [a; b] все промежуточные значения между своими наименьшим и наибольшим значениями.
- •Упражнения 4
- •Упражнения 5
- •Библиографический список
- •Часть 2
- •Глава 1. Дифференциальное исчисление………………………………………………….5
- •§1. Производная функции одной переменной
- •Правила дифференцирования
- •§2. Задачи, приводящие к понятию производной функци
- •§4. Основные теоремы о дифференцируемых функциях
- •§5. Исследование функций на монотонность и экстремум
- •Задачи на экстремум.
- •§6. Вогнутость и точки перегиба
- •Определение 6.Точки, в которых график функции меняет направление вогнутости называютсяточками перегиба.
- •Упражнения 1
- •Ответы к упражнениям 1
- •Глава 2. Интегральное исчисление
- •§1. Неопределенный интеграл
- •Правила интегрирования
- •Основные свойства неопределенных интегралов
- •§2. Методы интегрирования
- •3.Интегрирования по частям. Пусть u и V - дифференцируемые функции от х, тогда верно равенство
- •5. Интегрирование некоторых тригонометрических функций.
- •§3. Определенный интеграл
- •Свойства определенного интеграла
- •§4.Приложения определенных интегралов
- •1.Вычисление площади плоской фигуры, ограниченной линиями
- •§5. Несобственные интегралы
- •Упражнения 2
- •Ответы к упражнениям 2
- •Глава 3. Функции нескольких переменных
- •§1. Евклидово n-мерное пространство
- •§2. Экстремумы функций двух переменных
- •§3. Метод наименьших квадратов
- •Упражнения 3
- •Глава 4. Функции комплексного переменного
- •§1. Определение и геометрическое и изображение
- •Предел и непрерывность функции комплексного переменного
- •§2. Элементарные функции комплексного переменного
- •§3. Дифференцирование
- •Другие свойства
- •Геометрический смысл производной
- •Глава 5. Дифференциальные уравнения
- •§1. Дифференциальные уравнения 1-го порядка
- •Теорема о существовании решения задачи Коши
- •Методы интегрирования дифференциальных уравнений
- •§2. Дифференциальные уравнения 2-го порядка
- •Теорема существования решения задачи Коши
- •Методы понижения порядка.
- •§3. Линейные уравнения 2-го порядка
- •§4. Линейные уравнения с постоянными коэффициентами
- •Упражнения 5
- •Глава 8.Элементы теории вероятностей
- •§1.Определение вероятности и ее свойства
- •Свойства вероятности
- •§2. Повторные независимые испытания
- •§3. Случайные величины
- •Основные свойства функции распределения f(X)
- •Основные свойства плотности распределения f(X)
- •Свойства математического ожидания
- •Свойства дисперсии
- •Основные виды распределений
- •§4. Закон больших чисел
- •Приложение 1.Элементы комбинаторики Основные правила комбинаторики
- •Простейшие соединения
- •Упражнения 7
- •Упражнение 8
- •Библиографический список
- •Приложение 2. Математико-статистические таблицы
- •Глава 8. Введение в математическую статистику
- •§1. Выборочный метод
- •Основные виды распределений
- •Упражнение 8
Основные свойства логарифмов
1).
Основное
логарифмическое тождество: 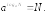
2).
Логарифм от 1 равен нулю:
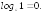
3).
Логарифм от основания равен единице:

4). Логарифм произведения равен сумме логарифмов:

5). Логарифм дроби равен разности логарифмов:

6). При логарифмировании степени логарифм умножается на ее показатель:
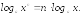
7). При логарифмировании корня логарифм делится на показатель корня:

5. Логарифмической функцией называется функция вида у= logax, которая каждому значению х ставит в соответствие логарифм по основанию а от х. Основание а является положительным и не равно единице.
Областью определения логарифмической функции logax является промежуток (0; + ); она неограниченная и может принимать любые значения от до +. При а > 1 функция logax возрастает от до + (в этом случае пишут: loga0 = и loga(+ = +. При а < 1 функция logax, убывает от + до (т.е. loga0 = + и loga(+ = ). При основании а = е 2,72 логарифмы logеx называются натуральными и обозначаются lnx . График у = ln x пересекает ось Ох под углом 45о.
у

Таблица
значений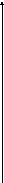
3
x y1 y2
0,25 -2 2
0,5 -1 1
1 0 0
2 1 -1
4 2 -2
8 3 -3

2
y1
= log2x


1
x 
0 1 2 3 4 5 6 7 8
-1
-2 y2
= log0,5x
-3
Рис. 3.
6. Тригонометрические функции.
1) синусом угла называется ордината точки М, обозначение: sin ;
2) косинусом угла называется абсцисса точки М, обозначение: cos;
3)тангенсом
называется
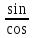
если сos
0, обозначение:
tg.
если сos
0, обозначение:
tg.
4)
котангенсом
называется
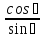
если
sin
0, обозначение:
ctg.
если
sin
0, обозначение:
ctg.
Y

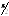
M(cos;
sin)


0 X
2

Рис. 4.
Из
пунктов 1), 2) данного определения следует,
что значения функций
sin
и cos
заключены в промежутке [1;
1]. Кроме того, эти значения повторяются,
когда точка М
делает полный оборот по окружности,
т.е. sin(+
sinи
сos(
сos.
При
= 00 точка
М
занимает крайнее правое положение, и
ее координаты равны (1; 0), поэтому сos00
1 и sin
00=
0.
При этом tg
00
=
 =
0, но значениесtg00
не определено.
При
= 900
М
занимает верхнее положение, и ее
координаты равны (0; 1), поэтому сos
900
0 и sin
900=
1. При этом
сtg
900
=
=
0, но значениесtg00
не определено.
При
= 900
М
занимает верхнее положение, и ее
координаты равны (0; 1), поэтому сos
900
0 и sin
900=
1. При этом
сtg
900
=
 =0,
но значениеtg900
не определено.
Аналогично
находятся значения данных функций в
других точках. В следующей таблице
приведены основные значения этих
функций.
=0,
но значениеtg900
не определено.
Аналогично
находятся значения данных функций в
других точках. В следующей таблице
приведены основные значения этих
функций.
Между собой данные функции связаны следующими равенствами, которые называются основными тригонометрическими тождествами:
sin2+
сos2
1; 1+ tg2= ;
1+сtg2
;
1+сtg2
tg=
tg= ;
ctg=
;
ctg=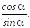
|
|
900 |
600 |
450 |
300 |
00 |
300 |
450 |
600 |
900 |
1200 |
1350 |
1500 |
1800 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
sin |
1 |
|
|
|
0 |
|
|
|
1 |
|
|
|
0 |
|
cos |
0 |
|
|
|
1 |
|
|
|
0 |
|
|
|
1 |
|
tg |
|
|
|
|
0 |
|
1 |
|
|
|
1 |
|
0 |
|
ctg |
0 |
|
1 |
|
|
|
1 |
|
0 |
|
1 |
|
|
Следующие формулы часто используются для преобразования сложных тригонометрических выражений.
Формулы приведения:
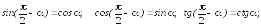

Формулы понижения степени:
сos2 sin2
sin2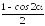
sinсos ;
cos2
sin2cos2
;
cos2
sin2cos2
Формулы преобразования произведения в сумму:
sinсos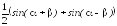
cosсos
sinsin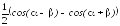 .
.
Теперь определяются числовые тригонометрические функции
6.Функцией y = sinx называется отображение, при котором каждому
значению х ставится в соответствие синус угла в х радиан. Областью определения этой функции является (; ), область значений [1; 1]. Как было отмечено выше, sinx – периодическая функция с наименьшим положительным периодом 2Ее график имеет следующий вид.
y 
1



.
x





1
Рис. 5.
7.Функцией y = cosx называется отображение, при котором каждому значению х ставится в соответствие косинус угла в х радиан. Областью определения этой функции является (; ), область значений [1; 1]. Как было отмечено выше, сosx – периодическая функция с наименьшим положительным периодом 2Ее график имеет следующий вид.
y 
1



.
x





1
Рис. 6.
8.Функцией
y
= tgx
называется
отображение, при котором каждому значению
х
ставится в соответствие тангенс угла
в х
радиан. Областью определения этой
функции являются интервалы вида
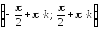 ,kZ.
Область значений (;
).
Функция tgx
также периодическая и ее наименьший
положительный период равен :
tg(x+)
=
tgx.Ее
график изображен на рис.7.
,kZ.
Область значений (;
).
Функция tgx
также периодическая и ее наименьший
положительный период равен :
tg(x+)
=
tgx.Ее
график изображен на рис.7.
у



. x






Рис. 7.