- •В.А.Ганов учебно-методический комплекс
- •280700.62 «Техносферная безопасность»
- •Оглавление
- •Пояснительная записка
- •1). Цели и задачи дисциплины, ее место в учебном процессе
- •2). Общие пояснения
- •2.Основные требования государственного образовательного стандарта
- •3.2. Содержание учебной дисциплины
- •4. Разделы учебной дисциплины, виды учебной деятельности и формы контроля
- •5. Самостоятельная работа студента
- •5.1. График самостоятельной работы студента
- •6. Оценочные средства для контроля успеваемости ирезультатов освоения учебной дисциплины
- •7.Литература
- •2.5.1. Основная литература
- •7. Материально-техническое обеспечение учебной дисциплины
- •2.6.1. Требования к аудиториям (помещениям, местам) для проведения занятий:
- •7.2. Требования к оборудованию рабочих мест преподавателя и обучающихся:
- •8.Тематический план (распределение часов курса по темам и видам работ):
- •1 Семестр
- •2 Семестр
- •3 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •1 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •2 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •3 Семестр
- •10.Контрольные задания и тесты
- •Вариант 2.
- •13.Какой из следующих определителей не равен нулю?
- •Вариант 2
- •Вариант 19
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 27
- •Утверждаю: Зав. Кафедрой_________________
- •11.1. Вопросы к экзамену по дисциплине «Высшая математика»,
- •8.1.2.Экзаменационные билеты по высшей математике
- •11.2.Экзаменационные вопросы
- •11.2.Экзаменационные билеты (2-й семестр)
- •8.3.1.Экзаменационные вопросы
- •8.3.2.Экзаменационные билеты по высшей математике 3-й семестр
- •Учебные пособия
- •Оглавление
- •Глава 1. Элементы линейной алгебры
- •§1. Числовые матрицы и определители
- •Основные свойства матриц
- •Основные свойства определителей
- •§2. Обратная матрица
- •§3. Системы линейных уравнений
- •2) Если определитель а равен нулю и хотя бы один из I отличен от нуля, то система (5) не имеет решений;
- •3) Если определитель а и все вспомогательные определители I равны нулю, то система (5) имеет бесконечное множество решений.
- •1) Если в (7) нет противоречий и число уравнений равно числу неизвестных, то система (3) имеет единственное решение;
- •2) Если (7) содержит противоречие, то система (3) не имеет решений;
- •3) Если в (7) нет противоречий, но число уравнений меньше числа неизвестных, то система (3) имеет бесконечное множество решений.
- •§4. Ранг матрицы и неопределенные системы
- •Упражнения 1
- •Глава 2. Аналитическая геометрия
- •§1. Декартова система координат
- •§2. Уравнение прямой линии на плоскости
- •§3. Кривые линий второго порядка
- •§4. Декартовы координаты и векторы в пространстве
- •2). Координаты точки деления отрезка в заданном отношении вычисляют по формулам:
- •§5. Скалярное произведение векторов
- •Свойства скалярного произведения
- •§6. Векторное и смешанное произведения
- •Свойства векторного произведения
- •§7. Плоскость и прямая линия в пространстве
- •2).Условие параллельности плоскостей:
- •Основное правило 1.
- •2).Условие параллельности прямых:
- •Основное правило 2.
- •Упражнения 2
- •Глава 3. Поверхности второго порядка
- •§1.Сферические, цилиндрические и конические поверхности
- •Частные случаи.
- •§2.Стандартные поверхности 2-го порядка
- •§3. Поверхности вращения
- •Упражнения 3
- •Глава 4. Комплексные числа
- •§1. Алгебраическая форма комплексного числа
- •§2. Тригонометрическая форма комплексного числа
- •Упражнения 4
- •Глава 5. Разложение рациональных дробей
- •Правило разложения правильной вещественной дроби на простейшие дроби.
- •Глава 6. Введение в математический анализ
- •§1. Числовые функции
- •§2. Простейшие функции
- •Основные свойства степеней
- •Основные свойства логарифмов
- •6. Тригонометрические функции.
- •Обратные тригонометрические функции.
- •§3. Бесконечные величины и предел функции
- •Свойства пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Теперь исходный предел равен: §4. Непрерывные функции
- •3) F(X) принимает на [a; b] все промежуточные значения между своими наименьшим и наибольшим значениями.
- •Упражнения 4
- •Упражнения 5
- •Библиографический список
- •Часть 2
- •Глава 1. Дифференциальное исчисление………………………………………………….5
- •§1. Производная функции одной переменной
- •Правила дифференцирования
- •§2. Задачи, приводящие к понятию производной функци
- •§4. Основные теоремы о дифференцируемых функциях
- •§5. Исследование функций на монотонность и экстремум
- •Задачи на экстремум.
- •§6. Вогнутость и точки перегиба
- •Определение 6.Точки, в которых график функции меняет направление вогнутости называютсяточками перегиба.
- •Упражнения 1
- •Ответы к упражнениям 1
- •Глава 2. Интегральное исчисление
- •§1. Неопределенный интеграл
- •Правила интегрирования
- •Основные свойства неопределенных интегралов
- •§2. Методы интегрирования
- •3.Интегрирования по частям. Пусть u и V - дифференцируемые функции от х, тогда верно равенство
- •5. Интегрирование некоторых тригонометрических функций.
- •§3. Определенный интеграл
- •Свойства определенного интеграла
- •§4.Приложения определенных интегралов
- •1.Вычисление площади плоской фигуры, ограниченной линиями
- •§5. Несобственные интегралы
- •Упражнения 2
- •Ответы к упражнениям 2
- •Глава 3. Функции нескольких переменных
- •§1. Евклидово n-мерное пространство
- •§2. Экстремумы функций двух переменных
- •§3. Метод наименьших квадратов
- •Упражнения 3
- •Глава 4. Функции комплексного переменного
- •§1. Определение и геометрическое и изображение
- •Предел и непрерывность функции комплексного переменного
- •§2. Элементарные функции комплексного переменного
- •§3. Дифференцирование
- •Другие свойства
- •Геометрический смысл производной
- •Глава 5. Дифференциальные уравнения
- •§1. Дифференциальные уравнения 1-го порядка
- •Теорема о существовании решения задачи Коши
- •Методы интегрирования дифференциальных уравнений
- •§2. Дифференциальные уравнения 2-го порядка
- •Теорема существования решения задачи Коши
- •Методы понижения порядка.
- •§3. Линейные уравнения 2-го порядка
- •§4. Линейные уравнения с постоянными коэффициентами
- •Упражнения 5
- •Глава 8.Элементы теории вероятностей
- •§1.Определение вероятности и ее свойства
- •Свойства вероятности
- •§2. Повторные независимые испытания
- •§3. Случайные величины
- •Основные свойства функции распределения f(X)
- •Основные свойства плотности распределения f(X)
- •Свойства математического ожидания
- •Свойства дисперсии
- •Основные виды распределений
- •§4. Закон больших чисел
- •Приложение 1.Элементы комбинаторики Основные правила комбинаторики
- •Простейшие соединения
- •Упражнения 7
- •Упражнение 8
- •Библиографический список
- •Приложение 2. Математико-статистические таблицы
- •Глава 8. Введение в математическую статистику
- •§1. Выборочный метод
- •Основные виды распределений
- •Упражнение 8
§4. Декартовы координаты и векторы в пространстве
Определение 11. Декартова система координат в пространстве это три занумерованные взаимно перпендикулярные числовые оси, с общим началом отсчета О. Первая ось обозначается ОХ и называется осью абсцисс, вторая ось ОY называется осью ординат, третья ось ОZ называется осью апликат. Декартовыми координатами точки М в пространстве называются координаты проекций этой точки на оси ОХ, ОY, ОZ. Обозначение: М(x; y; z).
Теорема 12. 1). Расстояние между двумя точками М1(x1; y1; z1) и М2(x2; y2; z2) находят по формуле:
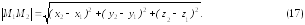
2). Координаты точки деления отрезка в заданном отношении вычисляют по формулам:
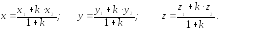
Пусть рассматривают какой-то процесс и в нем наблюдают некоторые величины, которые могут подразделять на два вида: скалярные и векторные.
Определение 12. Скалярной величиной называется величина, которая измеряются одним числом. Например: длина, площадь, объем, вес, температура, работа, энергия, доход – скалярные величины.
Определение
13. Векторные
величины
измеряются числом и направлением.
Например: сила, скорость, ускорение,
напряженность электрического поля –
векторные величины. Такие величины
удобно задавать направленными
отрезками,
которые имеют длину и направление и
изображаются стрелками. Эти направленные
отрезки называются векторами.
Они обозначаются буквами
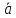 ,b,
,b,
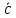 ,d
c
черточкой сверху или через
,d
c
черточкой сверху или через
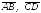 ,
где первая буква обозначает
начало
вектора и вторая буква обозначает конец
вектора.
Длина вектораa
или
,
где первая буква обозначает
начало
вектора и вторая буква обозначает конец
вектора.
Длина вектораa
или
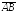 обозначается
обозначается
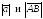 и называется такжемодулем
вектора.
и называется такжемодулем
вектора.
Два
вектора
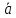 ,
,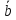 называютсяравными,
если они имеют одинаковые длины,
параллельны и направлены в одну сторону,
обозначение:
называютсяравными,
если они имеют одинаковые длины,
параллельны и направлены в одну сторону,
обозначение:
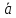 =
=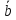 .
В данном определении не участвуют точки
приложения векторов
.
В данном определении не участвуют точки
приложения векторов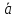 и
и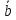 ,
это означает, что вектор не зависит от
своей точки приложения и его можно
перемещать параллельно самому себе. В
этом смысле рассматриваемые векторы
называютсясвободными
векторами.
Вектор, длина которого равна 0, называется
нуль-вектором
и обозначается
через 0,
его направление произвольное.
,
это означает, что вектор не зависит от
своей точки приложения и его можно
перемещать параллельно самому себе. В
этом смысле рассматриваемые векторы
называютсясвободными
векторами.
Вектор, длина которого равна 0, называется
нуль-вектором
и обозначается
через 0,
его направление произвольное.
Определение
14. Произведением
вектора
н
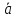 число k
называется вектор
k
число k
называется вектор
k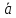 , длина
которого равна |k||
, длина
которого равна |k||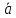 |
и, еслиk
> 0, то его
направление совпадает с направлением
|
и, еслиk
> 0, то его
направление совпадает с направлением
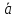 ,
а если k
< 0, то его направление противоположно
направлению
,
а если k
< 0, то его направление противоположно
направлению
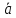 ,
(см. рис. 8). Вектор (1)
,
(см. рис. 8). Вектор (1)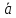 называется
противоположным
вектору
называется
противоположным
вектору
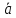 и обозначается
-
и обозначается
-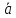 .
На рис.8 изображены:
.
На рис.8 изображены:
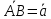 ,
,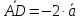 ,
,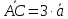 .
.
D
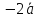 A
A
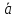 B
B
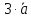 C
C

Рис.8.
Определение 15. Сложение двух и более векторов осуществляется по правилу многоугольника: первый вектор фиксируется, второй вектор параллельно самому себе перемещается в конец первого вектора, затем таким же образом третий вектор перемещается в конец второго вектора и т. д. После размещения всех векторов их суммой является вектор, начало которого совпадает с началом первого вектора и конец совпадает с концом последнего вектора (см. рис.9).
a2

a3
a1

a4

a1 +a2+a3+a4
Рис.9.
Операция сложения определяется также по правилу параллелограмма:
Пусть
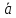 =
=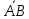 ,
,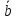 =
=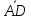 -
стороны параллелограммаABCD,
тогда
-
стороны параллелограммаABCD,
тогда
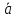 +
+
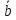 =
=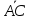 ,
при этом
,
при этом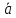
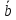 =
=
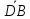 .
.
B
C 




A
D
Рис.10.
Пример
16. На трех
векторах(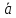 =
=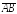 ,
(
,
(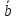 =
=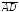 (
(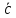 ,=
,=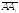 построен
параллелепипед.
Указать те его векторы-диагонали, которые
соответственно равны
построен
параллелепипед.
Указать те его векторы-диагонали, которые
соответственно равны
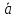 +
+
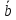 –
–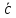 ,
,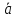 –
–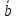 +
+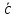 (см. рис.11).
(см. рис.11).
Решение.
Для первой комбинации выбирают вершину
А1,
в ней помещают вектор,
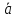 ,
который равен
,
который равен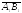 .
В вершинеB1
пристраивают вектор
.
В вершинеB1
пристраивают вектор
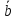 ,
который в
данном построении равен
,
который в
данном построении равен
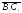 .
Теперь, в вершине C1
пристраивают вектор –
.
Теперь, в вершине C1
пристраивают вектор –
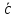 ,
который равен
,
который равен .
По правилу многоугольника, получилось,
что
.
По правилу многоугольника, получилось,
что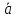 +
+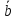 –
–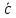 =
=
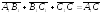 – искомый вектор-диагональ.
Аналогично
показывается, что комбинация
– искомый вектор-диагональ.
Аналогично
показывается, что комбинация
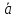 -
-
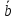 +
+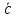 равна
равна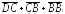 =
=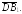
D1 N C1






A1
B1





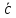 D C
D C
K
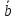 M
M
A
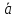 B
B
Рис.11.
Пример
17. Пусть в
примере 16 токи K,
M,
N
являются серединами ребер
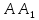 ,BC,
,BC,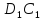 .
Выразить векторы AN,
NM,
K
.
Выразить векторы AN,
NM,
K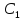 через векторы
через векторы
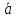 ,
,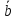 ,
,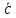 .
.
Решение.
По рис.11 вектор
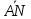 равен сумме
равен сумме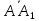 +
+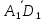 +
+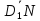 =
=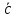 +
+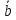 +
+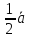 ;
;
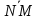 =
=
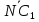 +
+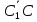 +
+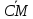 =
=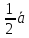
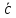
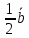 ;
;
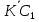 =
=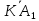 +
+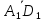 +
+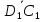 =
=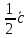
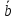
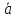 .
.
Геометрической
проекцией
точки
А
на числовую
ось ОХ
является основание А1
перпендикуляра,
опущенного из А
на эту ось (обозначение:
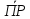 ОХ
А
= А1
. Точка А1
имеет на
оси ОХ
некоторую координату х,
эта координата называется алгебраической
проекцией
точки
А на числовую
ось ОХ,
обозначение:
ОХ
А
= А1
. Точка А1
имеет на
оси ОХ
некоторую координату х,
эта координата называется алгебраической
проекцией
точки
А на числовую
ось ОХ,
обозначение:
ПрОХ А = х.
Геометрической
проекцией вектора
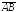 на числовую
ось ОХ
является вектор
на числовую
ось ОХ
является вектор
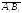 ,
гдеА1
=
,
гдеА1
=
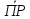 ОХ
А
и В1
=
ОХ
А
и В1
=
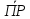 ОХ
В,
обозначение:
ОХ
В,
обозначение:
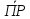 ОХ
ОХ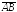 =
=
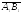 .
.
Алгебраической
проекцией вектора
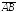 на числовую
ось ОХ
называется число (х2
– х1),
где х1
= ПрОХ
А
и х2
= ПрОХ
В,
обозначение:
ПрОХ
на числовую
ось ОХ
называется число (х2
– х1),
где х1
= ПрОХ
А
и х2
= ПрОХ
В,
обозначение:
ПрОХ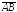 = (х2
– х1).
= (х2
– х1).
Ортом
оси ОХ
называется вектор
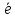 ,
имеющий длину 1 и направление, одинаковое
с осьюОХ.
,
имеющий длину 1 и направление, одинаковое
с осьюОХ.
Лемма
1. Геометрическая
проекция вектора
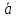 на ОХ равна произведению орта оси ОХ на
алгебраическую проекцию этого вектора
на ОХ:
на ОХ равна произведению орта оси ОХ на
алгебраическую проекцию этого вектора
на ОХ:
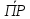 ОХ
ОХ
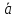 = ПрОХ
= ПрОХ
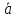
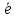
Доказательство.Рассматривается случай, изображенный на рис.12.
y
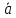 A
A
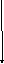
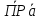



O
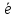 B
x
B
x
Рис. 12.
По
определению геометрической проекции,
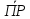 ОХ
ОХ
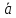 =
=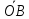 .
По определению, алгебраической проекции,ПрОХ
.
По определению, алгебраической проекции,ПрОХ
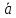 =
ПрОХ A
- ПрОХ
O
= ПрОХ
B
- ПрОХ
O
= ПрОX
=
ПрОХ A
- ПрОХ
O
= ПрОХ
B
- ПрОХ
O
= ПрОX
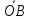 .
С другой
стороны, по предыдущим определениям,
ПрОХ
.
С другой
стороны, по предыдущим определениям,
ПрОХ
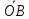 ∙
∙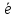 =
= .Следовательно,
.Следовательно,
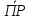 ОХ
ОХ
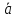 =
=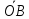 =
ПрОХ
=
ПрОХ
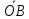 ∙
∙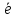 = ПрОХ
= ПрОХ
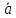
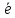 ,
что и требовалось доказать. Остальные
случаи рассматриваются аналогично
(см.[1. с.113]). С
помощью этой леммы легко доказываются
следующие свойства проекций векторов.
,
что и требовалось доказать. Остальные
случаи рассматриваются аналогично
(см.[1. с.113]). С
помощью этой леммы легко доказываются
следующие свойства проекций векторов.
1). Геометрическая проекция суммы векторов равна сумме геометрических проекций векторов, входящих в эту сумму:
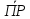 ОХ(
ОХ(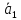 +
… +
+
… +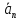 )
=
)
=
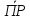 ОХ
ОХ
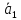 + … +
+ … +
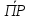 ОХ
ОХ
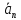 .
.
2). Алгебраическая проекция суммы векторов равна сумме алгебраических проекций векторов, входящих в эту сумму:
ПрОХ(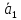 +
… +
+
… +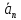 )
= ПрОХ
)
= ПрОХ
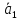 +… +
ПрОХ
+… +
ПрОХ
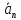 .
.
3). Геометрическая проекция произведения вектора на число k равна произведению геометрической проекции этого вектора на число k :
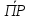 ОХ(k
ОХ(k
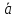 )
= k∙
)
= k∙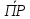 ОХ
ОХ
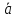 .
.
4). Алгебраическая проекция произведения вектора на число k равна произведению алгебраической проекции этого вектора на число k :
ПрОХ(k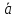 )
= kПрОХ
)
= kПрОХ
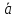 .
.
Определение
16. Пусть
ОХYZ
– декартова система координат в
пространстве и
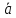 –
вектор.Координатами
–
вектор.Координатами
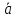 называются алгебраические проекции
этого вектора на оси координат.
называются алгебраические проекции
этого вектора на оси координат.
Используются
следующие обозначения для координат
вектора
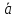 и самого вектора через его координаты:
и самого вектора через его координаты:
ах=
ПрОХ
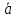 ,ау=
ПрОY
,ау=
ПрОY
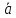 ,аz=
ПрОZ
,аz=
ПрОZ
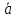 ,
,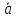 ={ах;
аy;
аz}.
={ах;
аy;
аz}.
Из
определения алгебраической проекции
следует, что если известны декартовы
координаты начала А(х1;
у1;
z1)
и конца В(х2;
у2;
z2)
вектора
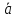 =
=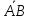 ,
то координаты
этого вектора находятся по формулам:
,
то координаты
этого вектора находятся по формулам:
ах= х2 – х1, ау= у2 – у1, аz= z2 – z1, (18)
т. е. от координат конца вычитаются координаты начала.
Если
М(х,
у,
z)
точка пространства, то вектор
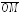 называется
радиусом-вектором
этой точки. Согласно предыдущим формулам,
координаты
называется
радиусом-вектором
этой точки. Согласно предыдущим формулам,
координаты
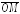 совпадают с координатами точкиМ
:
совпадают с координатами точкиМ
:
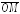 =
{х;
у;
z}.
Кроме того, в силу формулы (17), длина
вектора
=
{х;
у;
z}.
Кроме того, в силу формулы (17), длина
вектора
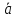 ={ах;
аy;
аz}
равна корню квадратному из суммы
квадратов его координат:
={ах;
аy;
аz}
равна корню квадратному из суммы
квадратов его координат:

Из указанных выше свойств легко выводятся следующие правила вычисления линейных операций через координаты векторов.
1). При умножении вектора на число k его координаты умножаются на k:
k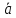 ={kах;
kay;
kaz}.
={kах;
kay;
kaz}.
2). При сложении векторов их координаты складываются:
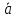 +
+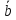 ={ах
+
bx;
аy
+
by;
аz
+
bz}.
={ах
+
bx;
аy
+
by;
аz
+
bz}.
Орты
координатных осей OX,
OY,
OZ
обозначаются через
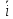 ,
,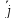 ,
,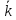 ,cоответственно.
Эти векторы имеют следующие координаты:
,cоответственно.
Эти векторы имеют следующие координаты:
i = {1; 0; 0}, j= {0; 1; 0},k= {0; 0; 1}.
Тогда, по лемме 1, произвольный вектор а ={ах; аy; аz} выражается линейно через i, j, k следующим образом:
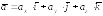 .
(20)
.
(20)
Пример
18. Даны
точки А(3;
2; 1) и В(6;
4;
3). Найти
координаты и длину вектора
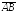 и выразить его линейно через орты.
и выразить его линейно через орты.
Решение. Применяют формулы (17) (19).