
- •В.А.Ганов учебно-методический комплекс
- •280700.62 «Техносферная безопасность»
- •Оглавление
- •Пояснительная записка
- •1). Цели и задачи дисциплины, ее место в учебном процессе
- •2). Общие пояснения
- •2.Основные требования государственного образовательного стандарта
- •3.2. Содержание учебной дисциплины
- •4. Разделы учебной дисциплины, виды учебной деятельности и формы контроля
- •5. Самостоятельная работа студента
- •5.1. График самостоятельной работы студента
- •6. Оценочные средства для контроля успеваемости ирезультатов освоения учебной дисциплины
- •7.Литература
- •2.5.1. Основная литература
- •7. Материально-техническое обеспечение учебной дисциплины
- •2.6.1. Требования к аудиториям (помещениям, местам) для проведения занятий:
- •7.2. Требования к оборудованию рабочих мест преподавателя и обучающихся:
- •8.Тематический план (распределение часов курса по темам и видам работ):
- •1 Семестр
- •2 Семестр
- •3 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •1 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •2 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •3 Семестр
- •10.Контрольные задания и тесты
- •Вариант 2.
- •13.Какой из следующих определителей не равен нулю?
- •Вариант 2
- •Вариант 19
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 27
- •Утверждаю: Зав. Кафедрой_________________
- •11.1. Вопросы к экзамену по дисциплине «Высшая математика»,
- •8.1.2.Экзаменационные билеты по высшей математике
- •11.2.Экзаменационные вопросы
- •11.2.Экзаменационные билеты (2-й семестр)
- •8.3.1.Экзаменационные вопросы
- •8.3.2.Экзаменационные билеты по высшей математике 3-й семестр
- •Учебные пособия
- •Оглавление
- •Глава 1. Элементы линейной алгебры
- •§1. Числовые матрицы и определители
- •Основные свойства матриц
- •Основные свойства определителей
- •§2. Обратная матрица
- •§3. Системы линейных уравнений
- •2) Если определитель а равен нулю и хотя бы один из I отличен от нуля, то система (5) не имеет решений;
- •3) Если определитель а и все вспомогательные определители I равны нулю, то система (5) имеет бесконечное множество решений.
- •1) Если в (7) нет противоречий и число уравнений равно числу неизвестных, то система (3) имеет единственное решение;
- •2) Если (7) содержит противоречие, то система (3) не имеет решений;
- •3) Если в (7) нет противоречий, но число уравнений меньше числа неизвестных, то система (3) имеет бесконечное множество решений.
- •§4. Ранг матрицы и неопределенные системы
- •Упражнения 1
- •Глава 2. Аналитическая геометрия
- •§1. Декартова система координат
- •§2. Уравнение прямой линии на плоскости
- •§3. Кривые линий второго порядка
- •§4. Декартовы координаты и векторы в пространстве
- •2). Координаты точки деления отрезка в заданном отношении вычисляют по формулам:
- •§5. Скалярное произведение векторов
- •Свойства скалярного произведения
- •§6. Векторное и смешанное произведения
- •Свойства векторного произведения
- •§7. Плоскость и прямая линия в пространстве
- •2).Условие параллельности плоскостей:
- •Основное правило 1.
- •2).Условие параллельности прямых:
- •Основное правило 2.
- •Упражнения 2
- •Глава 3. Поверхности второго порядка
- •§1.Сферические, цилиндрические и конические поверхности
- •Частные случаи.
- •§2.Стандартные поверхности 2-го порядка
- •§3. Поверхности вращения
- •Упражнения 3
- •Глава 4. Комплексные числа
- •§1. Алгебраическая форма комплексного числа
- •§2. Тригонометрическая форма комплексного числа
- •Упражнения 4
- •Глава 5. Разложение рациональных дробей
- •Правило разложения правильной вещественной дроби на простейшие дроби.
- •Глава 6. Введение в математический анализ
- •§1. Числовые функции
- •§2. Простейшие функции
- •Основные свойства степеней
- •Основные свойства логарифмов
- •6. Тригонометрические функции.
- •Обратные тригонометрические функции.
- •§3. Бесконечные величины и предел функции
- •Свойства пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Теперь исходный предел равен: §4. Непрерывные функции
- •3) F(X) принимает на [a; b] все промежуточные значения между своими наименьшим и наибольшим значениями.
- •Упражнения 4
- •Упражнения 5
- •Библиографический список
- •Часть 2
- •Глава 1. Дифференциальное исчисление………………………………………………….5
- •§1. Производная функции одной переменной
- •Правила дифференцирования
- •§2. Задачи, приводящие к понятию производной функци
- •§4. Основные теоремы о дифференцируемых функциях
- •§5. Исследование функций на монотонность и экстремум
- •Задачи на экстремум.
- •§6. Вогнутость и точки перегиба
- •Определение 6.Точки, в которых график функции меняет направление вогнутости называютсяточками перегиба.
- •Упражнения 1
- •Ответы к упражнениям 1
- •Глава 2. Интегральное исчисление
- •§1. Неопределенный интеграл
- •Правила интегрирования
- •Основные свойства неопределенных интегралов
- •§2. Методы интегрирования
- •3.Интегрирования по частям. Пусть u и V - дифференцируемые функции от х, тогда верно равенство
- •5. Интегрирование некоторых тригонометрических функций.
- •§3. Определенный интеграл
- •Свойства определенного интеграла
- •§4.Приложения определенных интегралов
- •1.Вычисление площади плоской фигуры, ограниченной линиями
- •§5. Несобственные интегралы
- •Упражнения 2
- •Ответы к упражнениям 2
- •Глава 3. Функции нескольких переменных
- •§1. Евклидово n-мерное пространство
- •§2. Экстремумы функций двух переменных
- •§3. Метод наименьших квадратов
- •Упражнения 3
- •Глава 4. Функции комплексного переменного
- •§1. Определение и геометрическое и изображение
- •Предел и непрерывность функции комплексного переменного
- •§2. Элементарные функции комплексного переменного
- •§3. Дифференцирование
- •Другие свойства
- •Геометрический смысл производной
- •Глава 5. Дифференциальные уравнения
- •§1. Дифференциальные уравнения 1-го порядка
- •Теорема о существовании решения задачи Коши
- •Методы интегрирования дифференциальных уравнений
- •§2. Дифференциальные уравнения 2-го порядка
- •Теорема существования решения задачи Коши
- •Методы понижения порядка.
- •§3. Линейные уравнения 2-го порядка
- •§4. Линейные уравнения с постоянными коэффициентами
- •Упражнения 5
- •Глава 8.Элементы теории вероятностей
- •§1.Определение вероятности и ее свойства
- •Свойства вероятности
- •§2. Повторные независимые испытания
- •§3. Случайные величины
- •Основные свойства функции распределения f(X)
- •Основные свойства плотности распределения f(X)
- •Свойства математического ожидания
- •Свойства дисперсии
- •Основные виды распределений
- •§4. Закон больших чисел
- •Приложение 1.Элементы комбинаторики Основные правила комбинаторики
- •Простейшие соединения
- •Упражнения 7
- •Упражнение 8
- •Библиографический список
- •Приложение 2. Математико-статистические таблицы
- •Глава 8. Введение в математическую статистику
- •§1. Выборочный метод
- •Основные виды распределений
- •Упражнение 8
Утверждаю: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 1
1.Решить дифференциальное уравнение: (x2 + y2 )dx + 2xydy = 0.
2.Решить дифференциальное уравнение: yy’’ =( y’)3.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 2
1.Решить
дифференциальное уравнение: y’
=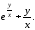
2.Решить дифференциальное уравнение: 3yy’’ + ( y’)2 =0 .
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 3
1.Решить дифференциальное уравнение: xdy ydx = ( x2 + y2).
2.Решить
дифференциальное уравнение: y’’
=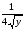 .
.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 4
1.Решить дифференциальное уравнение: y’ = x + y .
2.Решить дифференциальное уравнение: yy’’ + (y’)2 = 1.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 5
1.Решить дифференциальное уравнение: x2dy + (y 1)dx = 0.
2.Решить дифференциальное уравнение: y3y’’ = 4.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 6
1.Решить дифференциальное уравнение: xy’ + 4y + 4y =0.
2.Решить дифференциальное уравнение: 2xy’’ = y’.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 7
1.Решить дифференциальное уравнение: 2y’ + y = y3.
2.Решить дифференциальное уравнение: y2y’’ = (y’)3 .
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 8
1.Решить
дифференциальное уравнение: xy’
y
ln(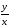 )
= 0.
)
= 0.
2.Решить дифференциальное уравнение: xy’’+ 2y’ + 2 = 0.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 9
1.Решить дифференциальное уравнение: 2ye2xdx + (e2x+ 1)dy = 0.
2.Решить дифференциальное уравнение: 3xy’’+ y’ = 0. .
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 10
1.Решить дифференциальное уравнение: : xy’ + 2y = 2y .
2.Решить дифференциальное уравнение: 3yy’’ = ( y’)2 .
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 11
1.Решить дифференциальное уравнение: y’ = x + y .
2.Решить дифференциальное уравнение: 3yy’’ + ( y’)2 =0 .
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 12
1.Решить
дифференциальное уравнение: xy’
y
ln(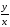 )
= 0.
)
= 0.
2.Решить дифференциальное уравнение: y2y’’ = (y’)3 .
3.Найти решение дифференциального уравнения y’’ + y = 2cos x, удовлетворяющее
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 15
1.Решить дифференциальное уравнение: (x2 + y2 )dx + 2xydy = 0.
2.Решить дифференциальное уравнение: yy’’ =( y’)3.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 16
1.Решить дифференциальное уравнение: y’ = ey/x + (y/x).
2.Решить дифференциальное уравнение: 3yy’’ + ( y’)2 =0 .
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 17
1.Решить дифференциальное уравнение: xdy ydx = ( x2 + y2).
2.Решить
дифференциальное уравнение: y’’
=
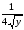 .
.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 18
1.Решить дифференциальное уравнение: y’ = x + y .
2.Решить дифференциальное уравнение: yy’’ + (y’)2 = 1.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 19
1.Решить дифференциальное уравнение: x2dy + (y 1)dx = 0.
2.Решить дифференциальное уравнение: y3y’’ = 4.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 13
1.Решить дифференциальное уравнение: xy’ + 4y + 4y =0.
2.Решить дифференциальное уравнение: 2xy’’ = y’.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 14
1.Решить дифференциальное уравнение: 2y’ + y = y3.
2.Решить дифференциальное уравнение: y2y’’ = (y’)3 .
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_____________
Контрольная работа №2 по математике.
Вариант № 20
1.Решить дифференциальное уравнение: xy’ y ln(y/x) = 0.
2.Решить дифференциальное уравнение: xy’’+ 2y’ + 2 = 0.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 21
1.Решить дифференциальное уравнение: 2ye2xdx + (e2x+ 1)dy = 0.
2.Решить дифференциальное уравнение: 3xy’’+ y’ = 0. .
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 23
1.Решить дифференциальное уравнение: : xy’ + 2y = 2y .
2.Решить дифференциальное уравнение: 3yy’’ = ( y’)2 .
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 24
1.Решить дифференциальное уравнение: y’ = x + y .
2.Решить дифференциальное уравнение: 3yy’’ + ( y’)2 =0 .
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой________________
Контрольная работа №2 по математике.
Вариант № 22
1.Решить
дифференциальное уравнение: xy’
y
ln(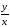 )
= 0.
)
= 0.
2.Решить дифференциальное уравнение: y2y’’ = (y’)3 .
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 25
1. Решить дифференциальное уравнение: 2ye2xdx + (e2x+ 1)dy = 0.
2. Решить дифференциальное уравнение: 3yy’’ = ( y’)2 .
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 26
1. Решить дифференциальное уравнение: y’ = ey/x + (y/x).
2. Решить дифференциальное уравнение: 2xy’’ = y’ .
АлтГУ .Специальности: "ТСБ" и "Химия".
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 27
1. Решить дифференциальное уравнение: xdy ydx = ( x2 + y2).
2. Решить дифференциальное уравнение: xy’’+ 2y’ + 2 = 0.
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 28
1. Решить дифференциальное уравнение: x2dy + (y 1)dx = 0.
2. Решить дифференциальное уравнение: y2y’’ = (y’)3
АлтГУ .Специальности: "ТСБ" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 29
1.Решить дифференциальное уравнение: xy’ + 4y + 4y =0.
2. Решить дифференциальное уравнение: yy’’ =( y’)3.
Контрольная работа по теме ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ТРЕБОВАНИЯ
УДОВЛЕТВОРИТЕЛЬО за №2-3
Хорошо за №1-4
ОТЛИЧНО за 1-4 с пояснениями
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 1
1.Решить дифференциальное уравнение: (x2 + y2 )dx + 2xydy = 0.
2.Решить дифференциальное уравнение: yy’’ =( y’)3.
3.Найти решение дифференциального уравнения y’’ 4y’ + 5y = xe2x, удовлетворяющее начальным условиям: y(0) = 1, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = 5x + 4y, y’ = 2x + 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 2
1.Решить дифференциальное уравнение: y’ = ey/x + (y/x).
2.Решить дифференциальное уравнение: 3yy’’ + ( y’)2 =0 .
3.Найти решение дифференциального уравнения y’’ 4y’ + 4y = e2x, удовлетворяющее начальным условиям: y(0) = 2, y’(0) = 8.
4. Решить систему дифференциальных уравнений: x’ = x + 3y, y’ = 3x + y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 3
1.Решить дифференциальное уравнение: xdy ydx = ( x2 + y2).
2.Решить дифференциальное уравнение: y’’ = 1/(4y ) .
3.Найти решение дифференциального уравнения y’’ 5y’ + 6y = (12x 7)ex, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = 2x + 8y, y’ = x 4y.
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 4
1.Решить дифференциальное уравнение: y’ = x + y .
2.Решить дифференциальное уравнение: yy’’ + (y’)2 = 1.
3.Найти решение дифференциального уравнения y’’ y’ = 5x2, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = x + 5y, y’ = 7x + 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 5
1.Решить дифференциальное уравнение: x2dy + (y 1)dx = 0.
2.Решить дифференциальное уравнение: y3y’’ = 4.
3.Найти решение дифференциального уравнения y’’ y’ 2y = 6x2, удовлетворяющее начальным условиям: y(0) 4, y’(0) = 1.
4. Решить систему дифференциальных уравнений: x’ = 2x + 3y, y’ = x + 4y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 6
1.Решить дифференциальное уравнение: xy’ + 4y + 4y =0.
2.Решить дифференциальное уравнение: 2xy’’ = y’.
3.Найти решение дифференциального уравнения y’’ + y = 2cos x, удовлетворяющее начальным условиям: y(0) = 1, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = x + 4y, y’ = 2x + 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 7
1.Решить дифференциальное уравнение: 2y’ + y = y3.
2.Решить дифференциальное уравнение: y2y’’ = (y’)3 .
3.Найти решение дифференциального уравнения y’’ 6y’ + 9y =10sin x, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = 4x + 6y, y’ = 4x + 2y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 8
1.Решить дифференциальное уравнение: xy’ y ln(y/x) = 0.
2.Решить дифференциальное уравнение: xy’’+ 2y’ + 2 = 0.
3.Найти решение дифференциального уравнения y’’ 4y = e2x, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = 5x + 8y, y’ = 3x + 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 9
1.Решить дифференциальное уравнение: 2ye2xdx + (e2x+ 1)dy = 0.
2.Решить дифференциальное уравнение: 3xy’’+ y’ = 0. .
3.Найти решение дифференциального уравнения y’’ 4y’ + 5y = 2x2e2x, удовлетворяющее начальным условиям: y(0) = 2, y’(0) = 3.
4. Решить систему дифференциальных уравнений: x’ = 2x + 5y, y’ = 4x + 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 10
1.Решить дифференциальное уравнение: : xy’ + 2y = 2y .
2.Решить дифференциальное уравнение: 3yy’’ = ( y’)2 .
3.Найти решение дифференциального уравнения y’’ 6y’ + 13y = 26x 1, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 1.
4. Решить систему дифференциальных уравнений: x’ = 3x + 5y, y’ = 3x + y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 11
1.Решить дифференциальное уравнение: y’ = x + y .
2.Решить дифференциальное уравнение: 3yy’’ + ( y’)2 =0 .
3.Найти решение дифференциального уравнения y’’ 5y’ + 6y = (12x 7)ex, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = 5x 4y, y’ = 2x 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 12
1.Решить дифференциальное уравнение: xy’ y ln(y/x) = 0.
2.Решить дифференциальное уравнение: y2y’’ = (y’)3 .
3.Найти решение дифференциального уравнения y’’ + y = 2cos x, удовлетворяющее начальным условиям: y(0) = 1, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = x 4y, y’ = 2x 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 15
1.Решить дифференциальное уравнение: (x2 + y2 )dx + 2xydy = 0.
2.Решить дифференциальное уравнение: yy’’ =( y’)3.
3.Найти решение дифференциального уравнения y’’ 4y’ + 5y = xe2x, удовлетворяющее начальным условиям: y(0) = 1, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = 5x + 4y, y’ = 2x + 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 16
1.Решить дифференциальное уравнение: y’ = ey/x + (y/x).
2.Решить дифференциальное уравнение: 3yy’’ + ( y’)2 =0 .
3.Найти решение дифференциального уравнения y’’ 4y’ + 4y = e2x, удовлетворяющее начальным условиям: y(0) = 2, y’(0) = 8.
4. Решить систему дифференциальных уравнений: x’ = x + 3y, y’ = 3x + y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 17
1.Решить дифференциальное уравнение: xdy ydx = ( x2 + y2).
2.Решить дифференциальное уравнение: y’’ = 1/(4y ) .
3.Найти решение дифференциального уравнения y’’ 5y’ + 6y = (12x 7)ex, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = 2x + 8y, y’ = x 4y.
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 18
1.Решить дифференциальное уравнение: y’ = x + y .
2.Решить дифференциальное уравнение: yy’’ + (y’)2 = 1.
3.Найти решение дифференциального уравнения y’’ y’ = 5x2, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = x + 5y, y’ = 7x + 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 19
1.Решить дифференциальное уравнение: x2dy + (y 1)dx = 0.
2.Решить дифференциальное уравнение: y3y’’ = 4.
3.Найти решение дифференциального уравнения y’’ y’ 2y = 6x2, удовлетворяющее начальным условиям: y(0) 4, y’(0) = 1.
4. Решить систему дифференциальных уравнений: x’ = 2x + 3y, y’ = x + 4y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 13
1.Решить дифференциальное уравнение: xy’ + 4y + 4y =0.
2.Решить дифференциальное уравнение: 2xy’’ = y’.
3.Найти решение дифференциального уравнения y’’ + y = 2cos x, удовлетворяющее начальным условиям: y(0) = 1, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = x + 4y, y’ = 2x + 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 14
1.Решить дифференциальное уравнение: 2y’ + y = y3.
2.Решить дифференциальное уравнение: y2y’’ = (y’)3 .
3.Найти решение дифференциального уравнения y’’ 6y’ + 9y =10sin x, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = 4x + 6y, y’ = 4x + 2y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 20
1.Решить дифференциальное уравнение: xy’ y ln(y/x) = 0.
2.Решить дифференциальное уравнение: xy’’+ 2y’ + 2 = 0.
3.Найти решение дифференциального уравнения y’’ 4y = e2x, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = 5x + 8y, y’ = 3x + 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 21
1.Решить дифференциальное уравнение: 2ye2xdx + (e2x+ 1)dy = 0.
2.Решить дифференциальное уравнение: 3xy’’+ y’ = 0. .
3.Найти решение дифференциального уравнения y’’ 4y’ + 5y = 2x2e2x, удовлетворяющее начальным условиям: y(0) = 2, y’(0) = 3.
4. Решить систему дифференциальных уравнений: x’ = 2x + 5y, y’ = 4x + 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 23
1.Решить дифференциальное уравнение: : xy’ + 2y = 2y .
2.Решить дифференциальное уравнение: 3yy’’ = ( y’)2 .
3.Найти решение дифференциального уравнения y’’ 6y’ + 13y = 26x 1, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 1.
4. Решить систему дифференциальных уравнений: x’ = 3x + 5y, y’ = 3x + y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 24
1.Решить дифференциальное уравнение: y’ = x + y .
2.Решить дифференциальное уравнение: 3yy’’ + ( y’)2 =0 .
3.Найти решение дифференциального уравнения y’’ 5y’ + 6y = (12x 7)ex, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = 5x 4y, y’ = 2x 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 21
1.Решить дифференциальное уравнение: xy’ y ln(y/x) = 0.
2.Решить дифференциальное уравнение: y2y’’ = (y’)3 .
3.Найти решение дифференциального уравнения y’’ + y = 2cos x, удовлетворяющее начальным условиям: y(0) = 1, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = x 4y, y’ = 2x 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 25
1. Решить дифференциальное уравнение: 2ye2xdx + (e2x+ 1)dy = 0.
2. Решить дифференциальное уравнение: 3yy’’ = ( y’)2 .
3. Найти решение дифференциального уравнения y’’ 6y’ + 9y =10sin x, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = 5x + 8y, y’ = 3x + 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 26
1. Решить дифференциальное уравнение: y’ = ey/x + (y/x).
2. Решить дифференциальное уравнение: 2xy’’ = y’ .
3. Найти решение дифференциального уравнения y’’ y’ 2y = 6x2, удовлетворяющее начальным условиям: y(0) 4, y’(0) = 1.
4. Решить систему дифференциальных уравнений: x’ = 2x + 3y, y’ = x + 4y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 27
1. Решить дифференциальное уравнение: xdy ydx = ( x2 + y2).
2. Решить дифференциальное уравнение: xy’’+ 2y’ + 2 = 0.
3. Найти решение дифференциального уравнения y’’ y’ = 5x2, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 0.
4. Решить систему дифференциальных уравнений: x’ = 4x + 6y, y’ = 4x + 2y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 28
1. Решить дифференциальное уравнение: x2dy + (y 1)dx = 0.
2. Решить дифференциальное уравнение: y2y’’ = (y’)3 .
3. Найти решение дифференциального уравнения y’’ 6y’ + 13y = 26x 1, удовлетворяющее начальным условиям: y(0) = 0, y’(0) = 1.
4. Решить систему дифференциальных уравнений: x’ = 2x + 5y, y’ = 4x + 3y .
АлтГУ .Специальности: "БЖД" и "Химия".
УТВЕРЖДАЮ: Зав. Кафедрой_________________
Контрольная работа №2 по математике.
Вариант № 29
1. Решить дифференциальное уравнение: xy’ + 4y + 4y =0.
2. Решить дифференциальное уравнение: yy’’ =( y’)3.
3. Найти решение дифференциального уравнения y’’ 4y’ + 5y = 2x2e2x, удовлетворяющее начальным условиям: y(0) = 2, y’(0) = 3.
4. Решить систему дифференциальных уравнений: x’ = x + 3y, y’ = 3x + y .
Самостоятельная работа 1 по теме ТЕОРИЯ ВЕРОЯТНОСТЕЙ
ТРЕБОВАНИЯ
УДОВЛЕТВОРИТЕЛЬО за №1-2
Хорошо за №1-3
ОТЛИЧНО за 1-3 с пояснениями
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 1.
1. Три стрелка производят по одному выстрелу в мишень. Вероятности попадания равны для первого стрелка 0,6, для второго 0, 5 и для третьего 0,2. Найти вероятности того, что будет хотя бы одно попадание.
2. Вероятность попадания в цель при одном выстреле равна 0,6. Найти вероятность того, что при пяти выстрелах будет не более трех промахов.
3. На склад поступило 8 шестеренок, среди которых 5 годных и 3 бракованных. Неудачу берут 4 шестеренки. Составить закон распределения случайной величины - числа годных шестеренок среди взятых. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 2. 1. В лотерее имеется 100 билетов, среди которых 10 выигрышных. Некто приобрел три билета. Какова вероятность, что он выиграет хотя бы по одному билету. 2. Известно, что в сбербанке в среднем 60 вкладчиков из 100 снимают начисленные проценты с вклада. Найти вероятность того, что из наудачу взятых пяти вкладчиков не менее половины снимут проценты со своих вкладов. 3. Производится стрельба из орудия по мишени до первого попадания. Вероятность попадания при первом выстреле равна 0,4, а при каждом следующем выстреле эта вероятность увеличивается на 0,1. Составить закон распределения случайной величины - числа израсходованных снарядов при 4 выстрелах. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 3.
1. Три спортсмена пытаются выполнить норму мастера спорта. Вероятность того, что первый спортсмен выполнит норму мастера, равна 0,9, второй - 0,7, третий - 0,8. Найти вероятность того, что норма мастера спорта будет выполнена хотя бы одним спортсменом.
2. Танк произвел 10 выстрелов по цели; вероятность попадания при каждом выстреле равна 0,4. Найти вероятность того, что число попаданий в цель будет заключено от 4 до 6.
3. Абонент забыл последнюю цифру нужного ему номера телефона, однако помнит, что она нечетная. Составить закон распределения случайной величины - числа сделанных им наборов номера телефона до попадания на нужный номер, если последнюю цифру он набирает наудачу и повторно ее уже не набирает. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 4.
1. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,9, во второе - 0,7, в третье - 0,8. Найти вероятность того, что хотя бы одно отделение получит газеты с опозданием.
2.Вероятность того, что шахматист в сеансе одновременной игры выиграет партию, равна 0,7. Найти вероятность того, что при игре с 9 партнерами он выиграет не менее 5 партий.
3. Участник олимпиады отвечает на три вопроса с вероятностями ответа на каждый соот-ветственно 0,6; 0,7; 0,4. За каждый верный ответ ему начисляется 5 баллов, за неверный списыва-ется 5 баллов. Составить закон распределения случайной величины - числа баллов, полученных участником олимпиады. . Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 5.
1. Клиент вложил деньги в акции двух предприятий, которые выдадут дивиденды с вероятностями 0,6 и 0,75 соответственно. Какова вероятность того, что клиент получит дивиденды хотя бы на одном предприятии?
2. Вероятность того, что в наудачу взятой семье есть дети, равна 0,8. Отобрано случайно 6 семей. Найти вероятность того, что среди этих семей детей имет хотя бы одна семья.
3.Студент выучил 30 вопросов из 35, включенных в билеты. Составить закон распределения случайной величины - числа положительных ответов на заданные ему три вопроса. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 6.
1. В ящике 50 лампочек мощностью 100Вт и 30 лампочек мощностью 40Вт. Найти вероятность того, что среди трех взятых наугад лампочек не более двух лампочек мощностью 100 Вт.
2. Вероятность выигрыша по одному билету денежно-вещевой лотереи составляет 0,2. Найти вероятность того, что из 6 купленных покупателем билетов выигрышными окажутся не менее 2.
3. Известно, что случайная величина Х, принимающая два значения х1 = 1 и х2 = 2, имеет математическое ожидание, равное 7/6. Найти вероятности, с которыми случайная величина Х принимает свои значения. Составить закон распределения случайной величина Х и найти ее дисперсию.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 7.
1. В цехе три участка. Вероятность невыполнения плана первым участком составляет 0,02, для второго - равна 0,05, и для третьего - 0,01. Найти вероятность того, что к моменту подведения итогов работы плановое задание будет выполнено всеми участками.
2. Вероятность того, что часы, сданные в ремонт, будут отремонтированы в срок, равна 0,9. Определить вероятность того, что из восьми сданных в ремонт часов более шести будут отремонтированы в срок.
3. Студент в поисках нужной книги обходит библиотеки, в которых он записан. Вероятность наличия книги в каждой из этих библиотек равна соответственно 0,7; 0,5; 0,8. Составить закон распределения случайной величины - числа библиотек , которые посетит студент, Найти математическое ожидание и дисперсию этой случайной величины, а также построить функцию ее распределения.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 8.
1.Среди 10 поступивших в ремонт часов 4 требуют замены маятника. Найти вероятность того, что среди взятых одновременно 3 часов хотя бы в одних часах требуется замена маятника.
2. Вероятность того, что изготовленная пара обуви высшего качества, равна 0,6. Найти вероятность того, что среди 8 взятых наудачу пар обуви окажутся высшего качества не менее 5 пар.
3. В автопробеге участвуют три автомобиля. Вероятность сойти с маршрута для первого автомобиля равна 0,16, для второго - 0,05 и для третьего - 0,1. Составить закон распределения случайной величины - числа машин, недошедших до финиша. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 9.
1. Среди изготовленных 20 пар обуви, 16 - первого сорта, а остальные - второго. Найти вероятность того, что среди взятых наудачу одновременно из этой партии трех пар обуви одна будет второго сорта.
2. Вероятность попадания в мишень при каждом выстреле равна 0,7. Производится 5 выстрелов. Определить вероятность того, что будет не менее 2 попаданий.
3. Брак в цехе составляет 0,05. Составить закон распределения случайной величины - числа годных изделий среди наудачу 4 взятых. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей.
Вариант 10.
1. В группе из 25 студентов, экзаменационную сессию на "хорошо" и "отлично" сдали 10 студентов. Определить вероятность того, что из двух наудачу вызванных студентов этой группы экзаменационную сессию на "хорошо" и "отлично" сдал хотя бы один студент.
2. Вероятность того, что автобус сломается в течение рабочего дня , равна 0,1. Найти вероятность того, что из 6 автобусов на линии сломаются не более 4.
3. Из орудия ведется стрельба по удаляющейся цели до первого попадания. Вероятность попадания при первом выстреле 0,6, при каждом следующем уменьшается на 0,1. Составить закон распределения случайной величины - числа промахов при имеющихся 4 снарядах. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет
Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 11.
1. В ящике находится 3 синих и 4 красных карандашей. Наудачу извлекаются 3 карандаша. Найти: вероятность того, что красных карандашей больше, чем синих.
2. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит неправильное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено более трех ошибочно упакованных пакетов.
3. При производстве некоторого изделия вероятность брака составляет 0,2. В этом случае предприятие терпит убыток в 10 тыс. руб. При изготовлении небракованного изделия прибыль предприятия составляет 20 тыс. руб. За день изготовлено 3 изделия. Составить закон распределения случайной величины – дневной прибыли предприятия. Найти математическое ожидание и дисперсию этой случайной величины
Алтайский государственный университет
Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 12.
1. Вероятность получить телефонный разговор в течение часа равна 0,7. Какова вероятность того, что из четырех абонентов более часа будут ожидать разговор менее двух абонентов?
2. Строительная фирма распространяет рекламные листки по почтовым ящикам. Опыт показывает, что примерно в одном случае из 2000 следует заказ. Найти вероятность того, что при размещении 100 000 листков число заказов будет находиться в границах от 45 до 55.
3. Вероятность того, что кредит размером до 1 млн. руб. не будет возвращен, равна 0,1, для кредита размером свыше 1 млн. руб. аналогичная вероятность равна 0,05. Банк выдал три кредита: в 500 тыс. руб. , 1,5 млн. руб. и 3 млн. руб. Составить закон распределения числа невозвращенных кредитов из этих трех выданных. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет
Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 13.
1. Курс акций каждого из двух предприятий возрастает на 10 пунктов с вероятностью 0,3 и убывает на 10 пунктов с вероятностью 0,2. Какова вероятность выйгрыша при покупке двух акций различных предприятий?
2.Аудиторную работу по теории вероятностей с первого раза успешно выполняют 50% студентов. Найти вероятность того, что из 400 студентов работу успешно выполнят не менее 180 студентов.
3. Составить закон распределения случайной величины – числа женщин среди пяти встреченных на улице людей, если вероятность встретить женщину на улице равна 0,6. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет
Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 14.
1. Покупатель решил обзвонить четыре магазина в поисках интересующего его товара. Вероятность обнаружить искомый товар в наудачу взятом магазине равна 0,3. Найти вероятность того, что покупателю придется сделать звонки в каждый магазин.
2. Вероятность нарушения герметичности у стеклянной банки с овощными консервами равна 0,0003. Найти вероятность того, что из 10000 банок герметичность нарушена хотя бы у трех банок.
3. Вероятность повышения цены на хлеб в текущем месяце равна 0,7, на масло – 0,8 и на яйца – 0,5. Составить закон распределения случайной величины – числа товаров, на которые будут повышены цены (среди рассматриваемых). Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет
Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 15.
1. Стрелок производит три выстрела по удаляющейся цели, причем вероятность поражения цели с первого раза равна 0,5 и при каждом следующем выстреле уменьшается на 0,1. Найти вероятность того, что цель будет поражена..
2. В отделе технического контроля проверяют 480 шестеренок. Вероятность бракованной шестеренки равна 0,1. Найти вероятность того, что число бракованных шестеренок не меньше 40 и не более 56.
3. Вероятность того, что посеянное семя взойдет, равна 0,5. Составить закон распределения случайной величины - числа взошедших семян среди 5 посеянных. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет
Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 16.
1. Некоторая компания имеет сеть дилеров на бирже. Вероятность того, что дилер будет играть удачно, равна 0,7. Найти вероятность того, что из пяти дилеров окажутся в убытке хотя бы двое (считается, что действия дилеров на бирже независмы друг от друга).
2. Вероятность того, что перфокарта набита оператором неверно, равна 0,1. Найти вероятность того, что из 230 перфокарт правильно набитых будет не менее 180 .
3. Из 10 вычислительных машинок две требуют наладки. Мастер выбирает три машинки. Составить закон распределения случайной величины – число машинок, требующих наладки, из трех отобранных. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет
Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 17.
1. В среднем 90% учащихся группы сдают зачет с первого раза. Найти вероятность того, что из 5 учащихся, сдававших зачет, с первого раза зачет сдадут не менее 4 человек.
2. Страховой компании имеется 500 клиентов. Каждый из них, страхуясь от несчастного случая, вносит 100 рублей. Вероятность несчастного случая 0,05, а страховая сумма , выплачиваемая пострадавшему, составляет 1 000 рублей. Какова вероятность того, что страховая фирма потерпит убыток (.т.е. выплата превысит 50 000 рублей).
3. Среди 10 билетов лотереи 3 выигрышных. Составить закон распределения случайной величины – число выйгрышных билетов среди трех взятых. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет
Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 18.
1. Среди 5 телевизоров, находящихся в продаже, 3 требуют дополнительной настройки. Найти вероятность того, что среди двух купленных телевизоров хотя бы один будет требовать дополнительной настройки.
2. Известно, что в среднем 60% всего числа изготавливаемых заводом телефонов являются 1-го сорта. Чему равна вероятность того, что в партии изготовленных 200 телефонов окажется 120 телефонов 1-го сорта?
3. Вероятность того, что наудачу взятая электрическая лампочка отработает гарантийный срок, равна 0,95. Составить закон распределения случайной величины – числа лампочек, которые отрабатывают гарантийный срок среди трех купленных. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет
Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 19.
1. По оценкам экспертов, вероятности банкротств для выделенных трех предприятий, производящих однотипную продукцию, равны соответственно 0,1, 0,2, 0,3. Найти вероятность банкротства не менее 2 предприятий.
2. В отделе технического контроля проаеряют 500 изделий. Вероятность того, что изделие бракованное, равна 0,05. Найти вероятность того, что число бракованных изделий среди проверенных не менее 20 и не более 30.
3. Из 30 экзаменационных вопросов студент подготовил 20. Составить закон распределения случайной величины – числа подготовленных вопросов среди трех вопросов экзаменационного билета. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет
Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 20.
1. На автомобиле установлены два противоугонных устройств, вероятности отключения которых равны 0,02 и 0,01 соответственно. Найти вероятность включения сигнала «тревоги» при угоне.
2. Вероятность того, что абонент наберет ошибочный телефонный номер, принимается для каждого абонента равной 0,001. Определить вероятность того, что среди 500 произведенных независимо друг от друга вызовов окажется не менее двух ошибочных.
3. Абонент забыл последнюю цифру нужного номера, но помнит, что она не менее 4. Найти закон распределения случайной величины - числа наборов телефонного номера до нахождения нужного номера, если последняя цифра набирается наугад из возможных (отвергнутая цифра повторно не набирается). Найти математическое ожидание и дисперсию этой случайной величины.
Методические указания к решению задач по теор.вер.
Вариант 1
1.Обозначим через А1, А2, А3события: 1-й,2-й,3-й стрелок попал в мишень. По условию Р(А1)=0,6, Р(А2)=0,5 и Р(А3)=0,2. Пусть В=»хотя бы одно попадание», рассмотрим противоположное событиеВ=А1А2А3. Эти события независимые, так как их вероятности не зависят отдругих событий. Поэтому Р(В)=Р(А1А2А3)= Р(А1)Р(А2)Р(А3)=(10,6)(,5)(10,2)= 0,16. Тогда Р(В)=10,16=0,84. Ответ: 0,84.
2. Пусть А="промах при одном выстреле",тогда Р(А)= 1 - 0,6 = 0,4 - это постоянное число, значит здесь схема повторных независимых испытаний, число испытаний n = 5, p=0,4, q=0,6 и можно применять формулу Бернулли Рn(m) = Cnmpmqn-m. Пусть В обозначает " при пяти выстрелах будет не более трех промахов". Противоположное событиеВ означает,что буде 4 или 5 промахов. Тогда m=4 или m=5. Эти события несовместные, поэтому P(В) = C54p4q1+ C55p5q0= 50,44 0,6 + 0,45=0,087040,087.. Теперь,Р(В) =1P(В)= 10,087 = 0,913.Ответ:)вероятность того, что будет не более трех промахов0,913.
3. Пусть Х = число годных шестеренок из 4. Тогда Х принимает значения 1,2,3,4. Событие Х=1 означанет, что одна шестеренка годная (это 5 случаев) и 3 шестеренки бракованные (это число сочетаний из 3 по 3). Тогда Р(Х=1) = С51С33/ С84 = 5/70=1/14. Событие Х=2 означанет, что две шестеренки годные (это число сочетаний из 5 по 2 случаев) и 2 шестеренки бракованные (это число сочетаний из 3 по 2). Тогда Р(Х=2)=С52С32/С84=3/7. Событие Х=3 означанет, что три шестеренки годные (это число сочетаний из 5 по 3 случаев) и 1 шестеренки бракованные (это число сочетаний из 3 по 1). Р(Х=3) = С53С31/С84= 3/7. Событие Х=4 означанет, что четыре шестеренки годные (это число сочетаний из 5 по 4 случаев). Р(Х=4) = 1/14.
Закон распределения имеет вид Х 1 2 3 4
Р 1/14 3/7 3/7 1/14
М(Х)=5/2=2,5. М(Х2)=95/14. D(X)= 95/14(2,5)2=15/280,538.
Вариант 2.
1.Обозначим через А1, А2, А3события: 1-й,2-й,3-й билет выйгрышный. Требуется найти вероятность события В= «хотя бы один билет выйгрышный» .Рассмотрим противоположное событие:В=»1-й,2-й,3-й билет не выйграли», это равноВ=А1А2А3. Эти события зависимые, поэтому Р(В)=Р(А1А2А3)= Р(А1)РА1(А2)РА1А2(А3). По формуле Р=m/nнаходим Р(А1)= (90/100), Далее, пусть событиеА1произошло, тога Р(А2)= (89/99). Далее, пусть событияА1 иА2произошли, тога Р(А3)= (88/98). Получили Р(В)= (90/100)(89/99)(88/98)0,727. Тогда Р(В)10,727=0,273. Ответ:0,273.
2. Пусть событие А равно «Вкладчик снимает начисленные проценты с вклада». По условию за Р(А) можно взять 60/100=0,6. Эта вероятность одинаковая для каждого вкладчика, поэтому здесь схема повторных независимых испытаний. число испытаний n = 5, p=0,6, q=0,4 и можно применять формулу Бернулли Рn(m) = Cnmpmqn-m. Пусть В обозначает "Из пяти не менее половины вкладчиков снимут проценты" ,это означает, что событие А наступит либо 3 раза, либо 4 раза, либо 5 раз. т.е. m = 3,4,5.Это попарно несовместимые события, поэтому по теореме сложения вероятность суммы этих событий равна сумме их вероятностей P(В)=P(m=3 + m=4 +m=5 ) =P5(3)+P5(4) +P5(5) = C530,630,42+C540,640,41+C550,650,40=0,3456 + 0,2592+0,07776 = 0,682560,683.Ответ:0,683.
3. Пусть Х = «число израсходованных снарядов при 4 выстрелах»Тогда Х принимает значения 1,2,3,4. Событие означает попадание при 1-м выстреле, по условию Р(Х=1) = 0,4. Событие Х=2 означает промах при 1-м выстреле, и попадание при 2-м выстреле. Эти события независмые, так как их вероятности не зависят от наступления другого из этих событий, по условию Р(Х=2 ) = (1 – 0,4)(0,4 + 0,1) = 0,3. Событие Х=3 означает промах при 1-м и 2-м выстрелах, и попадание при 2-м выстреле. Эти события независмые, так как их вероятности не зависят от наступления другого из этих событий, по условию получаем Р(Х=3 ) = (1 – 0,4)(1 0,5)(0,5+0,1) = 0,18. . Событие Х=4 означает промах при 1-м, 2-м и 3-м выстрелах. Эти события независмые, так как их вероятности не зависят от наступления другого из этих событий, по условию получаем Р(Х=4 ) = (1 – 0,4)(1 – 0,5)(1-0,6) = 0,12.
Закон распределения имеет вид Х 1 2 3 4
Р 0,4 0,3 0,18 0,12
М(Х) = 2,02. М(Х2)=5,14. D(X)= 5,14 – 2,022(2,5)2=1,05961,060.
Вариант 3.
1 . Пусть А1, А2,А3обозначают события:"Первый, второй, третий спортсмен выполнит норму мастера" соответственно. По условию Р(А1)=0,9, P(А2)=0,7, P(А3)= 0,8 .Указанные здесь события независимые, так как их вероятности не зависят от наступления другого из этих событий. Пусть D = "норму мастера выполнит хотя бы один спортсмен" Рассмотрим противоположное событиеD = "все спортсмены не выполнят норму мастера". это записываетсяD2 =А1А2А3.Тогда P(D)= P(А1А2А3) =.( 10,9) ·( 10,7)·(10,8)Теперь, Р(D)=10,006 = 0,994.Ответ:Вероятность, что норму мастера выполнит хотя бы один спортсмен = 0,994.
2. Пусть А="попадание при одном выстреле",тогда Р(А)=0,4 - это постоянное число, значит здесь схема повторных независимых испытаний, число испытаний n = 10, p=0,4, q=0,6 и можно применять формулу Бернулли Рn(m) = Cnmpmqn-m. ПустьВобозначает "число попаданий в цель будет заключено от 4 до 6", это означает,что попаданий будет либо 4, либо 5,либо 6, т.е. m = 4,5,6.Это попарно несовместимые события, поэтому по теореме сложения вероятность суммы этих событий равна сумме их вероятностей P(В) =P(m=4 + m=5 +m=6 ) =P10(4)+P10(5) +P10(6) = C1040,440,66+ C1050,450,65+ C1060,460,64 0,2508 + 0,2007+0,1115=0,563.Ответ:вероятность того,что число попаданий в цель будет от 4 до 6,0,563.
Вариант 3.
3. Пусть Х = число сделанных наборов до попадания на нужный номер. Тогда Х может принимать значения 1,2,3,4,5. Событие Х=1 означает, что номер отгадан с 1-го раза, тогда По формуле Р=m/nнаходим Р(Х=1)= 1/5=0,2. Событие Х=2 означает, что 1-й раз он не отгадал и отгадал 2-й раз. Тогда По формуле Р=m/nнаходим Р(Х=2)=(4/5)(1/4)=0,2. Событие Х=3 означает, что 1-й и 2-й раз он не отгадал и отгадал 3-й раз. Тогда аналогично находим Р(Х=3)=(4/5)(3/4)(1/3)=0,2. Событие Х=4 означает, что 1-й, 2-й и 3-й раз он не отгадал и отгадал 4-й раз. Тогда аналогично находим Р(Х=4)=(4/5)(3/4)(2/3)(1/2)=0,2. Событие Х=5 означает, что 1-й, 2-й, 3-й и 4-й раз он не отгадал и отгадал 5-й раз. Тогда Р(Х=5)=(4/5)(3/4)(2/3)(1/2)(1/1)=0,2.Закон распределения имеет вид: Х 1 2 3 4 5
Р 0,2 0,2 0,2 0,2 0,2
Математическое ожидание равно М(Х)=10,2+20,2+30,2+40,2+50,2=3. Дисперсия равна 0,8.
Вариант 4.
1. Пусть А1, А2,А3обозначают события: "Первое, второе, третье отделение получит газеты вовремя " соответственно. По условию Р(А1)=0,9, P(А2)=0,7, P(А3)= 0,8.Указанные здесь события независимые, так как их вероятности не зависят от наступления другого из этих событий. Пусть С = "хотя бы одно отделение получит газеты с опозданием". Рассмотрим противоположное событиеС= "все отделение получит газеты вовремя". это записываетсяС= А1А2А3 . Так как множители независимые события, то Р(С) = Р(А1)Р(А2)Р(А3) =0,90,70,8=0,504Теперь,Р(С)=1Р(С)=10,504= 0,496.Ответ:Вероятность, что хотя бы одно отделение получит газеты с опозда-нием=0,496.
2..Пусть А="шахматист в сеансе одновременной игры выиграет партию",тогда Р(А)=0,7- это постоянное число для каждой партии, значит здесь схема повторных независимых испытаний, число испытаний n = 9, p=0,7, q=0,3 и можно применять формулу Бернулли Рn(m) = Cnmpmqn-m, где m - число наступлений события А. ПустьСобозначает событие "при игре с 9 партнерами шахматист выиграет не менее 5 партий". Это означает,что он выйграет либо 5, либо 6,либо 7, либо 8, , либо 9 партий,т.е. m = 5,6,7,8,9. Это попарно несовместимые события, поэтому по теореме сложения вероятность суммы этих событий равна сумме их вероятностей P(С)=P(m=5+ m=6 +m=7 + m=8+ m=9) =P9(5)+P9(6) +P9(7)+P9(8)+P9(9) =C950,750,34+C960,760,33+C970,770,32 +C980,780,31+C990,790,30 1260,1681+ 840,11760,027 +360,08240,09 +90,05760,3+10,040310,1716+0,2667+0.2670 + 0,1555+0,04030,901.Ответ: )вероятность того, что шахматист выиграет не менее 5 партий0,901.
3. Пусть Х = число баллов, полученных участником олимпиады. Тогда Х может равняться -15,-5,5,15. Пусть А1,А2,А3обозначают соответственно события "участник олимпиады ответил на 1-й,2-й,3-й вопрос". Указанные здесь события независимые, так как их вероятности не зависят от наступления других событий. Р(А1)=0,6, Р(А2)=0,7, Р(А3)=0,4. Событие Х=-15 означает, что Участник олимпиады на все вопросы не ответил, это записывается в видеА1А2А3.По теореме умножения для независимых событий Р(Х=-15)= Р(А1А2А3)= Р(А1)Р(А2)Р(А3)=(1- 0,6)(1- 0,7)(1- 0,4)=0,072. Cобытие Х=-5 означает,что Участник олимпиады ответил только на один вопрос, это записывается в виде А1А2А3 +А1А2А3+А1А2А3. Здесь каждое слагаемое попарно несовместимо с другими слагаемыми, так как они содержат множители вида либо Аi,либоАi. Тогда по теореме сложения и по теореме умножения получаем: Р(Х=-5) = Р(А1А2А3+А1А2А3+А1А2А3) = Р(А1А2А3) + Р(А1А2А3)+ Р(А1А2А3) = Р(А1)Р(А2)Р(А3)+Р(А1)Р(А2)Р(А3)+Р(А1)Р(А2)Р(А3)=0,6(10,7)(10,4)+(10,6)0,7(10,4)+(10,6)(10,7)0,4 =0,324.Событие Х=5 означает,что Участник олимпиады ответил только на два вопроса, это записывается в виде А1А2А3+А1А2А3+А1А2А3.Здесь каждое слагаемое попарно несовместимо с другими слагаемыми, так как они содержат множители вида либо Аi,либоАi. Тогда по теореме сложения и по теореме умножения получаем: Р(Х=5) = Р(А1А2А3+ А1А2А3+А1А2А3) = Р(А1А2А3) + Р(А1А2А3)+ Р(А1А2А3) = Р(А1)Р(А2)Р(А3)+ Р(А1)Р(А2)Р(А3)+Р(А1)Р(А2)Р(А3)= 0,60,7(10,4)+0,6(10,7)0,4+(10,6)0,70,4 = 0,436. Cобытие Х = 15 означает,что Участник олимпиады ответил на все три вопроса. Это записывается так:А1А2А3. По теореме умножения Р(Х=3 )= Р(А1А2А3)= Р(А1)Р(А2)Р(А3)=0,60,70,4=0,168.
Закон распределения имеет вид: Xi -15 -5 5 15
Математическое ожидание находится -------------------------------------------------------
по формуле: pi 0,072 0,324 0,436 0,168
M(X) = p1X1+ ... + рnXn = -150,072 -50,324 + 50,436 + 150,168 =2. Дисперасия равна (-15)20,072+(-5)20,324 + 520,436 + 1520,168 – 22 = 69.Ответ: M(X) =2.D(X) =2.
Вариант 5.
1. Пусть А и В обозначают события"Первое предприятие выдаст дивиденты" и "второе предприятие выдаст дивиденты", соответственно.Тогда Р(А)=0,6 и Р(В)=0,75. Событие "Хотя бы на одном предприятии выдадут дивиденды" означает AB+AB+AB.События AB,AB,AB попарно несовместимые,так как в них имеются множители, являющиеся противоположными событиями: A иA , В иB, Кроме того А и В независимые,так как их вероятности не зависят от наступления другого события.
Поэтому по теореме сложения для несовместимых и по теореме умножения для независимых событий и по свойству Р(В) = 1Р(В) получаем Р(AB+AB+AB) =P(AB) +P(AB) +P(AB)=P(A)(1- P(B))+(1-P(A))P(B) +P(A)P(B) = 0,60,25+0,40,75+0,60,75=0,9.Ответ:вероятность того, что "Хотя бы на одном предприятии выдадут дивиденды"=0,9.
2. Пусть А="в наудачу взятой семье есть дети".Тогда Р(А) = 0,8 - это постоянное число, значит здесь схема повторных независимых испытаний и можно применять формулу Бернулли. Пусть В="среди этих семей детей имеет хотя бы одна", рассмотрим противоположное событие B="все семьи не имеют детей". Последнее означает, что m=0,поэтому Р(B) =P6(0) = C600,800,26= 0,0000640,0001.Теперь Р(В)10,0001=0,99991.Ответ:вероятность того, что "среди этих семей детей имеет хотя бы одна"1.
3.Пусть Х = число положительных ответов на заданные три вопроса. Тогда Х может принимать значения: 0,1,2,3. Пусть А,В и С обозначают события "студент ответил на первый вопрос", "студент ответил на второй вопрос". и "студент ответил на третий вопрос". Событие Х=0 означает, что студент не ответил на первый, второй и третий вопросы,т.е.А.В.С .Тогда Р( Х=0) =Р(А.В.С). По теореме умножения Р(А.В)= Р(А).РА(В) .РА В(С) . Вероятность событияА равна отношению числа невыученных вопросов к общему числу вопросов: Р(А)=5/35=1/7. Условная вероятность РА(В) равна отношению числа невыученных вопросов к общему числу вопросов при условии, что один невыученный вопрос уже был рассмотрен:РА(В)=4/34=2/17. Условная вероятность РА В(С) равна отношению числа невыученных вопросов к общему числу вопросов при условии, что два невыученный вопрос уже были рассмотрены: РА В(С) =3/33=1/11. Теперь,
Р( Х=0) = 1/7.2/17.1/1102.Событие Х=1 означает, что студент ответил только на один вопросы, т.е. А.В.С +А.В.С +А.В.С . Тогда Р( Х=1) = Р(. А.В.С +А.В.С +А.В.С). События . А.В.С ,А.В.С ,А.В.С несовместимые, так как в них имеются множители, A иA , В иB, , С иС. Поэтому по теореме сложения для несовместимых событий и по свойству 3 получаем Р( Х=1)= Р(. А.В.С) +Р(А.В.С ) +Р(А.В.С). По теореме умножения Р(. А.В.С) = Р( А).РА(В) .РА В(С). Как в предыдущем случае находим Р(. А.В.С)= 30/35.5/34.4/3315, Р( Х=1)3.0,015=0,045. Событие Х=2 означает, что студент ответил на два вопроса и не ответил на один, т.е. А.В.С +А.В.С + А.В.С. Тогда Р( Х=2) = Р(.А.В.С +А.В.С + А.В.С). По теореме умножения, как в предыдущих случаях, находим
Р(. А.В.С)= 30/35.29/34.5/33111, и Р( Х=2)3.0,111=0,333. Событие Х=3 означает, что студент ответил на три вопроса, т.е. А.В.С. Тогда Р( Х=3) = Р(.А.В.С). По теореме умножения, как в предыдущих случаях, находим
Р(. А.В.С)= 30/35.29/34.28/33620. Закон распределения имеет вид
Хi0 1 2 3
рi0,002 0,045 0,333 0,620
Математическое ожидание находится по формуле M(X) = p1X1+ ... + рnXn 00,002 + 10,045 + 20,333 + 30,62 =2,571 .Дисперсия вычисляется по формуле D(X) = M(X2) - M2(X) . Закон распределения для Х2 имеет вид
Тогда М(Х2)00,002 + 10,045 +40,333+90,62=6,957. D(X)6,957- 2,5712 0,347.Ответ:M(X)2,571, D(X)0,347. .
Вариант 6.
1. Пусть А1,А2,А3, обозначают события :1-я, 2-я, 3-я лампочка оказалась мощностью 100 Вт, соответственно. а) Событие В=" трех взятых наугад лампочек: не более двух лампочек мощностью 100 Вт"." и рассмотрим противоположноеС="среди трех взятых наугад лампочек более двух лампочек мощностью 100 Вт.", это означает, что все три лампочки мощностью 100 ВТ». Это записывается в виде А1A2A3. По теореме умножения для зависимых событий получаем: Р(А1A2A3) = Р(А1)РА1(А2)РА1А2(А3). Вероятность события равна отношению числа благоприятствующих случаев к общему числу случаев: Р=m/n. Для каждого Аi "случаем" является взять какую-нибудь лампочку, а "благоприятствующим случаем" является взять лампочку мощностью 100 Вт. При выборе 1-й лампочки имеется 50+30=80 возможностей и 50 возможностей взять лампочку мощностью 100 Вт , тогда Р( А1)=50/80. Условная вероятность РА1(А2) вычисляется при предположении, что событие А1произошло, т.е. 1-я взятая лампочка мощностью 100 ВТ. Тогда осталось 79 лампочек и среди них 49 мощностью 100 Вт. Поэтому РА1(А2)=49/79. Условная вероятность РА1А2(А3) вычисляется при предположении, что события А1и А2 произошли, т.е. 1-я и 2-я взятые лампочки мощностью 100 Вт. Тогда осталось 78 лампочек и среди них 48 мощностью 100 Вт. Поэтому РА1А2(А3)=48/78.Теперь вероятность Р(В)= 50/8049/7948/780,239. По свойству вероятности Р(С)= 1Р(С)10,239Ответ:Вероятность того, что среди трех взятых наугад лампочек: не более двух лампочек мощностью 100 Вт..
2. Пусть А="выигрыша по одному билету денежно-вещевой лотереи ", тогда Р(А)=0,2 - это постоянное число для каждого билета, значит здесь схема повторных независимых испытаний, число испытаний n = 6, p=0,2, q=1 - 0,2 = 0,8 и можно применять формулу Бернулли Рn(m) = Cnmpmqn-m, где m - число наступлений события А. Пусть В обозначает "из 6 купленных покупателем билетов выигрышными окажутся не менее 2". Противоположное событиеВ означает,что из 6 купленных покупателем билетов выигрышными окажутся либо 0, либо 1 билетов, т.е. m=0 или m =1.Это несовместимые события, поэтому Р(В) = P(m=0 + m=1)= P(m=0) + P(m=1) = Р6(0)+Р6(1)= C600,200,86+ С610,210,85 110,2621 + 60,23277= 0,65534 . Теперь, Р(В)=1P(В) = 1 - 0,65534= 0,344660,345.Ответ:вероятность того, что из 6 купленных покупателем билетов выигрышными окажутся не менее 2,0,345.
Вариант 6.
3. Известно, что случайная величина Х, принимающая два значения х1 = 1 и х2 = 2, имеет математическое ожидание, равное 7/6.Найти вероятности, с которыми случайная величина Х принимает свои значения. Составить закон распределения случайной величина Х и найти ее дис-персию.Решение.Закон распределения случайной величины Х имеет вид
xi1 2
pip1p2
По основному свойству закона распределения p1+p2=1. Математическое ожидание равно сумме произведений значений случайной величины на вероятности этих значений: М(Х)=1p1+ 2p2
Получаем
систему: p1 +
p2 = 1,
1p1+ 2p2 = 7/6.
Решаем: вычтем первое уравнение из второго p2=1/6. тогда p1=5/6.
Теперь закон распределения случайной величины Х имеет вид xi1 2
pi5/6 1/6
Дисперсия равна D(Х) = M(Х2) - (M(Х))2Находим M(Z2) = 125/6 +
221/6=1,5. Тогда D(Х)=1,5 – (7/6)2 0,139. .Ответ:p1=5/6, p2=1/6; D(Х) 0,139.
Вариант 7.
1. Событие А=«плановое задание будет выполнено всеми участками» означает, что каждый участок выполнит задание. Эти события независимые, так как их вероятности независят от других событй. Тогда Р(А) = 0,980,950,99=0,921690,922. Ответ:0,922.
2. Обозначим через А = "часы, сданные в ремонт, будут отремонтированы в срок". Вероятность А равна Р(А) = 0,9 - это постоянная величина для всех чаов, значит здесь схема повторных независимых испытаний, число испытаний равно n=8, Событие "из восьми сданных в ремонт часов более шести будут отремонтированы в срок" означает,что 7 или 8 часов будут отремонтированы в срок, т.е. m = 7 или m = 8. Эти события несовместимые, поэтому вероятность суммы равна сумме вероятностей. Р(m= 7или m=8) = P8(7) + P8(8). Применим формулу Бернулли Рn(m) = Cnm · pm·qn-m. Здесь n=8, p = 0,9, q= 1 - 0,9 = 0,1 Получаем Р(m = 7 или m=8) = P8(7) + P8(8) = C87 ·0,97·0,1 + C88·0,98·0,10 0,3826+0,4305 = 0,81310,813.Ответ:вероятность того, что из восьми сданных в ремонт часов более шести будут отремонтированы в срок0,813.
3. Пусть Х = число библиотек , которые посетит студент, Тогда Х может равняться 1,2,3. Пусть А1, А2, А3обозначают соответственно события "студент нашел нужную книгу в первой, второй, третьей библиотеке" соответственно. Указанные здесь события независимые, так как их вероятности не зависят от наступления другой событий. Р(А1)=0,7, Р(А2)=0,5 , Р(А3)=0,8. Событие Х=1 означает, что все саженцы не прижились, это записывается в видеА1А2А3. Cобытие Х=1 означает, что книга найдена в первой библиотеке, тогда его вероятность равна Р(А1)=0,7. Событие Х=2 означает, что либо не в первой библиотеке книги не было и во второй библиотеке книга найдена. Это записывается в виде:А1А2.Тогда Р(Х=2 )= Р(А1А2).По теореме умножения Р(А1А2)= Р(А1)Р(А2)=(1- 0,7)0,5=0,15.Cобытие Х = 3 означает,что в первых двух библиотеках книги не было.Это записывается так:А1А2А3. По теореме умножения Р(Х=3 )= Р(А1А2А3)= Р(А1)Р(А2)Р(А3)=0,30,5=0,15.
Закон распределения имеет вид: Xi 1 2 3
Математическое ожидание находится ----------------------------------
по формуле: pi 0,7 0,15 0,15
M(X) = p1X1+ ... + рnXn =10,7 + 20,15 + 30,15 = 1,45 .Дисперсия вычисляется по формуле D(X) = M(X2) - M2(X) .
М(Х2)= 10,7 + 40,15 +90,15 =2,65. D(X) = 2,65 - 1,452 = 0,5475.
Вариант 8.
1. Пусть А1,А2,А3обозначают соответственно события " 1-е, 2-е, 3-и часы требуют замены маятника. Пусть С= "хотя бы в одних часах требуется замена маятника". Противоположное событиеС="все взятые часы не требуют замены маятника"=А1А2А3. Здесь зависимые события, поэтому по теореме умножения получаем: Р(А1А2А3) =Р(А1)РА1(А2)РА1А2(А3). Вероятность событияА1равна отношению числа благоприятствующих случаев к общему числу случаев: Р=m/n." случаем" является взять какие-нибудь часы, "благоприятствующим случаем" является взять часы, нетребующие замены маятника. При выборе первых часов имеется 10 возможностей, и взять часы, не требующие замены маятника 6 возможности ,тогда Р( А1)=6/10.Условная вероятность РА1(А2)=m/n вычисляется при предположении, что событиеА1произошло, т.е. первые часы нетребуют замены маятника. Тогда осталось 9 часов и среди них 5 не требуют замены маятника. Поэтому РА1(А2)=5/9. Условная вероятность РА1А2(А3)=m/n вычисляется при предположении, что событияА1иА2 произошли, т.е. первые и вторые часы 2-я не требуют замены маятника. Тогда осталось 8 часов и среди них 4 не требуют замены маятника. Поэтому РА1А2(А3)=4/8.Подставим найденные величины Р(А1А2А3) = (6/10)(5/9)(4/8) =1/6. Теперь, Р(С)=1- Р(С)=1- 1/6= 5/6 .Ответ:вероятность того, что среди взятых одновременно 3 часов хотя бы в одних часах требуется замена маятника, равна 5/6.
2. Пусть А="изготовленная пара обуви высшего качества", тогда Р(А)=0,6 - это постоянная вероятность для каждой пары, значит здесь схема повторных независимых испытаний, число испытаний n = 8, p=0,6,q=0,4 и можно применять формулу Бернулли Рn(m) = Cnmpmqn-m. Пусть С="среди 8 взятых наудачу пар обуви окажутся высшего качества не менее 5 пар", это означает, что пар обуви высшего качества будет либо 5, либо 6, либо 7, либо 8 ,
т.е. m = 5,или m =6, или m =7,или m =8 . Это попарно несовмести-мые события, поэтому по теореме сложения вероятность суммы этих событий равна сумме их вероятностей P(С) = P(m=5+m=6+m=7+m=8) = P8(5)+P8(6)+P8(7)+P8(8) = C850,650,43+C860,660,42 + C870,670,41 + C880,680,40 560,07780,064+280,04670,16+80,02800,4+10,016810,2788 + 0,2092+0,0896+0,01680,59450,594. Ответ: вероятность того, что среди 8 взятых наудачу пар обуви окажутся высшего качества не менее 5,0,594.
3. В автопробеге участвуют три автомобиля. Вероятность сойти с маршрута для первого автомобиля равна 0,16, для второго - 0,05 и для третьего - 0,1. Составить закон распределения числа машин, недошедших до финиша. Найти математическое ожидание и дисперсию этой слу-чайной величины. Решение. Х - число машин, недошедших до финиша. Тогда Х может принимать значе-ния 0,1,2,3. Находим вероятности этих значений. P(Х=0)=0,840,950,9= 0,7182; P(Х = 1) = 0,160,950,9+0,840,050,9+0,840,950,1=0,1368+0,0378+ 0,0798=0,2544;
P(Х =2)=0,160,050,9 + 0,160,950,1+0,840,050,1=0,0072+0,0152+0,0042=0,0266; P(Х = 3)
=0,160,050,1=0,0008.
|
X |
0 |
1 |
2 |
3 |
|
P |
0,7182 |
0,2544 |
0,0266 |
0.0008 |
M(X)=00,71820,2544+20,0266+30,0008=0,31; M(X2)=00,7182+0,2544+40,0266+90,0008=0,368;
D(X)=0,368 0,312=0,2719.
Вариант 9.
1. Пусть А = "одна пара обуви второго сорта и остальные первого сорта)". Простым событием является взять 3 пары обуви из 20. Это равно числу сочетаний по 3 из 20 = С203. Благоприятствующий случай – это взять две пары первого сорта и одну пару второго сорта, это равно произведению число сочетаний из 16 по 2 и число сочетаний из 4 по 1, т.е. C162·C41Тогда Р(А) = C162·C41/C203 =(1615/2)(4/1)/(201918/6)0,421.
2. Пусть событие А="попадание при одном выстреле". По условию Р(А)=0,7 - постоянная вероятность для каждого выстрела. Значит, имеем схему повторных независимых испытаний: число испытаний - это число выстрелов, n=5. р=Р(А)=0,7, q=1 - р=0,3. Пусть m - число попаданий. Требуется найти вероятность того, что m=2 или m=3, или m=4, или m=5. Эти события попарно несовместимые, поэтому по теореме сложения P(m=2 или m=3,или m=4,или m=4, или m=5)= P(m=3) +P(m=4)+P(m=5).Число испытаний небольшое,поэтому применяем формулу Бернулли: Рn(m) = Cnm · pm·qn-m. Получаем P5(2) + P5(3) + P5(4) +P5(5) = C52 ·0.72·0,33+C53 ·0.73·0,32 + C54·0,74·0,3 + C55·0,75·0,30 =10·0,49 ·0,027 + 10·0,343·0,09 +5·0,2401·0,3 + 1·0,16807·1 = 0,1323 + 0,3087+ 0,36015 + 0,16807 =0,969220,969.Ответ:вероятность того, что будет не менее 2 попаданий,0,969.
3. Пусть Х - число годных изделий среди наудачу взятых 4; Х может принимать значения 0,1,2,3,4.Обозначим А="взятое изделие является годным", тогда Р(А)=95:100=0,95 - это постоянная вероятность для всех изделий, значит здесь схема повторных независимых испытаний, Х имеет биномиальное распределение , поэтому вероятность события Х=m находится по формуле Бернулли: P(Х=m)= Рn(m)=Cnmpmqnm. Здесь n=4, p=0,95, q=0,05. Тогда P(Х=0)=P4(0)=C400,9500,0540,0000; P(Х=1) = P4(1) = C410,9510,053 = 40,950,0001250,0005; P(Х=2) = P4(2) =C420,9520,052 = 60,9025 0,0135; P(Х=3) = P4(3) = C430,9530,0540,85740,050,1715; P(Х=4) = P4(4) =C440,9540,05010,81451 = 0,8145.
Закон распределения имеет вид -----------------------------------------------------------------
таблицы, в которой указаны ! Х ! 0 1 2 3 4
все возможные значения Х и вероятности !----!------------------------------------------------------------
этих значений ! Р ! 0,0000 0,0005 0,0135 0,1715 0,8145
!----!-----------------------------------------------------------
Математическое ожидание М(Х) = 00,0000 + 10,0005+20,0135 +30,1715+40,8145=3,8. Дисперсия равна D(X)= M(X2) - (M(X))2= 00,0000+10,0005 + 40,0135 +90,1715 +160,8145 - (3,8)2=14,63 - (3,8)2 = 0,19. ! Р !
Ответ:М(Х)=3,8, D(X)=0,19
Вариант 10.
1.Пусть А1, А2обозначают соответственно события "1-й студент сдал сессию на "хорошо" и "отлично","2-й студент сдал сессию на "хорошо" и "отлично". в) Обозначим через С="хотя бы один студент сдал экзаменационную сессию на "хорошо" и "отлично", рассмотрим противоположное событиеС="оба студента не сдали экзаменационную сессию на "хорошо" и "отлично", это равноС=А1.А2 . Здесь зависимые события, поэтому по теореме умножения получаем: Р(А1А2) = Р(А1)Р А1(А2)Вероятность события равна отношению числа благоприятствующих случаев к общему числу случаев: Р=m/n. Для каждогоАi "случаем" является вызвать какого-нибудь студента из 25,а "благоприятствующим случаем" является вызвать студента из 15, не сдавших сессию на "хорошо" и "отлично" При выборе первого студента имеется 25 возможностей и вызвать студента из 15, не сдавших сессию на "хорошо" и "отлично", 15 возможностей, тогда Р(А1) = 15/25. Условная вероятность Р А1(А2) = m/n вычисляется при предположении, что событиеА1произошло, т.е. первый студент не сдал сессию на "хорошо" и "отлично" .Тогда осталось 24 студента и среди них 14 студентов, не сдавших сессию на "хорошо" и "отлично".Поэтому Р А1(А2) = 14/24.
Подставим найденные величины : Р(А1А2) ==(15/25)(14/24) = 0,35. Теперь, Р(С) = 1Р(С) = 10,35 = 0,65.Ответ:вероятность того, что хотя бы один студент сдал экзаменационную сессию на "хорошо" и "отлично" = 0,65.
2. Пусть А= "автобус сломается в течение рабочего дня", тогда Р(А)=0,1. Эта вероятность постоянна для каждого автобуса, значит здесь схема повторных независимых испытаний, число испытаний n=6, р=0,1, q=0,9, m - число наступлений события А, можно применять формулу Бернулли: Рn(m)=Cnmpmqnm. Пусть В="из 6 автобусов на линии сломаются не более 4". Рассмотрим противоположное событиеВ ="из 6 автобусов на линии сломаются более 4 ", это означает, что m=5 или m=6.Эти события несовместимые, поэтому P(В)=Р(m=5 или m=6)=P6(5)+P6(6) = C650,150,91+C660,160,90 60,000010,9 + 10,0000011 = 0,000055.Тогда P(В)=1P(В) = 10,0000551.Ответ: 1.
3. Пусть Х = число промахов при имеющихся 4 снарядах. Тогда Х может равняться 0,1,2,3,4. Пусть А1,А2,А3,А4обозначают соответственно события "промах при первом, втором, третьем,четвертом выстрелах". Указанные здесь события не зависимые, так как их вероятности не зависят от наступления другий событий. Р(А1)=10,6=0,4, Р(А2)=10,5=0,5 , Р(А3)=10,4=0,6, Р(А4)=10,3=0,7.Событие Х=0 означает, что попадание было при первом выстреле, это записывается в видеА1.Тогда Р(Х=0)=Р(А1)=0,6. Cобытие Х=1 означает,что при первом выстреле был промах и при втором - попадание. Это записывается в виде А1А2. Здесь множители являются независимыми событиями, поэтому Р(Х=1)= Р(А1)Р(А2) = 0,4( 10,5 )=0,2. Событие Х=2 означает,что при первом и втором выстрелах были промахи и при третьем - попадание. это записывается А1А2 А3 . Р(Х=2 )= Р(А1А2А3). Рассуждая как в предыдущих случаях, находим Р(Х=2) = Р(А1) Р(А2)Р(А3) = 0,40,5(10,6) = 0,08. Cобытие Х = 3 означает, что при первом, втором, третьем выстрелах промахи и при четвертом - попадание. это записывается А1А2А3 А4 . Тогда Р(Х=3) = Р(А1А2А3А4 )=0,40,50,6(10,7) = 0,036.Cобытие Х = 4 означает, что при всех выстрелах промах и это записывается А1А2А3А4 . Тогда Р(Х=4) =Р(А1А2А3А4 ) =0,40,50,60,7= 0,084.
--------------------------------------------------------------------
Закон распределения имеет вид: Xi 0 1 2 3 4
Математическое ожидание находится - --------------------------------------------------------------------
по формуле: pi 0,6 0,2 0,08 0,036 0,084
M(X) = p1X1+ ... + рnXn = --------------------------------------------------------------------
00,6 +10,2+20,0+30,036+40,084 =0,804. Дисперсия вычисляется по формуле D(X) =
M(X2)M2(X) . Закон распределения для Х2 имеет вид
------------------------------------------------------- Тогда М(Х2)= 00,6 + 10,2 +40,08 +90,036+
Xi20 1 4 9 16 160,084 = 2,188 . D(X) = 2,188 - 0,8042 1,5416.
-------------------------------------------------------
pi 0,6 0,2 0,08 0,036 0,084
------------------------------------------------------- Ответ:M(X) = 0,804 , D(X)1,5416.
Вариант 11.
1.Вероятность того, красных карандашей больше 0,629.
2. Пусть А= пакет содержит неправильное число денежных знаков. По условию Р(А)=0,0001 – это для каждого пакета. Поэтому здесь СПИ, при этом можно применять формулу Пуасона, Находим = 40000,0001 = 4 < 10. Пусть В= при проверке будет обнаружено более трех ошибочно упакованных пакетов, Рассмотрим противоположное событие , его вероятность равна Р(В)= Р(m=0)+H(m=1)+H(m=2)+H(m=3)= 0,0183+0,0733+0,1465+0,1954=0,4335. Теперь Р(В)= 1- 0,4335=0,5665.
3. Х =Дневная прибыль предприятия. М(Х)=28; D(Х)=273,6.
|
Х |
-20 |
10 |
40 |
|
Р |
0,04 |
0,32 |
0,64 |
Вариант 12.
1. вероятность того, что из четырех абонентов более часа будут ожидать разговор менее двух абонентов 0,652.
2.
Пусть А= следует заказ на рекламный
листок. По условию Р(А)=1:2000 = 0,0005 – это
для каждого листка. Поэтому здесь СПИ,
но при этом нельзя применять формулу
Пуасона, ибо =
100 0000,0005
= 50> 10. Применим формулу Муавра-Лапласа:
Пусть В= при размещении 10 000 листков
число заказов будет находиться в границах
от 45 до 55.
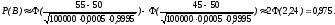 Рассмотрим
противоположное событие , его вероятность
равна Р(В)=
Р(m=0)+H(m=1)+H(m=2)+H(m=3)=
0,0183+0,0733+0,1465+0,1954=0,4335/
Рассмотрим
противоположное событие , его вероятность
равна Р(В)=
Р(m=0)+H(m=1)+H(m=2)+H(m=3)=
0,0183+0,0733+0,1465+0,1954=0,4335/
3. Х = число невозвращенных кредитов из этих трех выданных. М(Х)=0,2; D(Х)=0,185.
|
Х |
0 |
1 |
2 |
3 |
|
Р |
0,81225 |
0,17575 |
0,01175 |
0,00025 |
Вариант 13.
1. вероятность выйгрыша при покупке двух акций =0,09.
2.
Пусть А= студент аудиторную работу по
теории вероятностей с первого раза
успешно выполняет. По условию Р(А)=50:100
= 0,5 – это для каждого студента. Поэтому
здесь СПИ, Применим формулу Муавра-Лапласа:
Пусть В= из 400 студентов работу успешно
выполнят не менее 180 .
 Рассмотрим
противоположное событие , его вероятность
равна Р(В)=
Р(m=0)+H(m=1)+H(m=2)+H(m=3)=
0,0183+0,0733+0,1465+0,1954=0,4335/
Рассмотрим
противоположное событие , его вероятность
равна Р(В)=
Р(m=0)+H(m=1)+H(m=2)+H(m=3)=
0,0183+0,0733+0,1465+0,1954=0,4335/
3. Х = число встреченных женщин среди 5; . М(Х) =3; D(Х)=1,2.
|
Х |
0 |
1 |
2 |
3 |
4 |
5 |
|
Р |
0,0102 |
0,0768 |
0,2304 |
0,3456 |
0,2592 |
0,0772 |
Вариант 14.
1. вероятность того, что покупателю придется сделать звонки в каждый магазин 0,343.
2. Пусть А= нарушение герметичности у стеклянной банки с овощными консервами. По условию Р(А)=0,0001 – это для каждой банки. Поэтому здесь СПИ, при этом можно применять формулу Пуассона, Находим = 100000,0003 = 3 < 10. Пусть В= из 10000 банок герметичность нарушена хотя бы у трех банок, Рассмотрим противоположное событие , его вероятность равна Р(В)= Р(m=0)+Р(m=1)+Р(m=2)= 0,0498+0,1494+0,2240=0,4232. Теперь Р(В)= 1 0,4232=0,5768.
3. Х = число товаров, на которые будут повышены цены. М(Х)=2; D(Х)=0,62.
|
Х |
0 |
1 |
2 |
3 |
|
Р |
0,03 |
0,22 |
0,47 |
0,28 |
Вариант 15.
1. вероятность того, что цель будет поражена = 0,79.
2.
Пусть А= шестеренка бракованная. По
условию Р(А)=0,1 – это для каждой банки.
Поэтому здесь СПИ, Пусть В= из 480 шестеренок
число бракованных шестеренок не меньше
40 и не более 56. Каждое испытание – это
рассмотрение одной шестеренки, поэтому
число испытаний n=480,
р=0,1, q=0,9,
и если m=числу
бракованных шестеренок, то Р(В)=
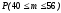 Здесьnpq=4800,10,9=43,2>20.
Можно применять формулу Муавра-Лапласа:
Здесьnpq=4800,10,9=43,2>20.
Можно применять формулу Муавра-Лапласа:
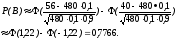
3. Х = число взошедших семян среди 5 посеянных. М(Х)=2,5; D(Х)=1,25.
|
Х |
0 |
1 |
2 |
3 |
4 |
5 |
|
Р |
0,03125 |
0,15625 |
0,31250 |
0,31250 |
0,15250 |
0,03125 |
Вариант 16.
1. вероятность того, что из пяти дилеров окажутся в убытке хотя бы двое 0,47178.
2.
Пусть А= перфокарта набита оператором
верно. По условию Р(А)= 1 -0,1=0,9 – это для
каждой перфокарты. Поэтому здесь СПИ,
Пусть В = из 230 перфокарт правильно
набитых будет не менее 210. Каждое испытание
– это рассмотрение одной перфокарты,
поэтому число испытаний n=230,
р=0,9, q=0,1,
и если m=числу
верных перфокарт, то Р(В)=
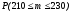 Здесьnpq=2300,90,1=20,7>20.
Можно применять формулу Муавра-Лапласа:
Здесьnpq=2300,90,1=20,7>20.
Можно применять формулу Муавра-Лапласа:
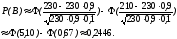
3. Х =число машинок, требующих наладки, из трех отобранных. М(Х) 0,601; D(Х)=0,374.
|
Х |
0 |
1 |
2 |
|
Р |
0,467 |
0,467 |
0,067 |
Вариант 17.
1.
Решение.
Пусть А= учащийся сдал зачет с первого
раза. По условию Р(А) = 0,9, значит здесь
схема повторных испытаний, и требуется
найти
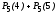 . По формуле Бернулли это равно
. По формуле Бернулли это равно
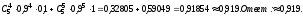
2.
Решение. Пусть А= наступление несчастного случая. По условию Р(А)=0,05 – это для каждого клиента. Поэтому здесь СПИ, Пусть В = страховая фирма потерпит убыток. Пусть m=число страховых случаев. Каждое испытание – это рассмотрение одного клиента, поэтому число испытаний n=500, р=0,05, q=0,95. Тогда
В
= (m51),
требуется найти Р(В)=
 Здесьnpq=5000,050,95=23,75>20.
Можно применять формулу Муавра-Лапласа:
Здесьnpq=5000,050,95=23,75>20.
Можно применять формулу Муавра-Лапласа:
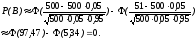
3.
Решение. Пусть Х = число выйгрышных
билетов среди трех взятых.Тогда Х
принимает значения 0, 1, 2,3. Вероятность
события Х=0 равна
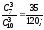 Вероятность события Х=1 равна
Вероятность события Х=1 равна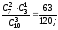 Вероятность события Х=2 равна
Вероятность события Х=2 равна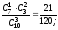 Вероятность события Х=3 равна
Вероятность события Х=3 равна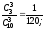 Тогда закон распределения имеет вид:
Тогда закон распределения имеет вид:
|
Х |
0 |
1 |
2 |
3 |
|
Р |
35/120 |
63/120 |
21/120 |
1/120 |
Отсюда получаем: М(Х) = 0,9 ; D(Х)=0,035.
Вариант 18.
1. вероятность того, что среди двух купленных телевизоров хотя бы один будет требовать дополнительной настройки =0,9.
2.
Пусть А=Изготовленный заводом телефон
являются 1-го сорта.. По условию Р(А)=0,60
– это для каждого телефона. Поэтому
здесь СПИ, Пусть В = В партии изготовленных
200 телефонов окажется 120 телефонов 1-го
сорта. Пусть m=число
телефонов 1-го сорта. Каждое испытание
– это рассмотрение одного телефона,
поэтому число испытаний n=200,
р=0,6, q=0,4.
Тогда В = (m=120),
требуется найти Р(В). Здесь
npq=2000,60,4=48>20.
Можно применять локальную формулу
Муавра-Лапласа:
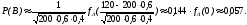
3. Х =число лампочек, которые отрабатывают гарантийный срок среди трех купленных. М(Х) =2,85; D(Х)=0,1425.
|
Х |
0 |
1 |
2 |
3 |
|
Р |
0,000125 |
0,007125 |
0,135375 |
0,857375 |
Вариант 19.
1. вероятность банкротства не менее 2 предприятий=0,994.
2.
Пусть А= изделие бракованное. По условию
Р(А)=0,05 – это для каждого изделия. Поэтому
здесь СПИ, Пусть В = число бракованных
изделий среди проверенных не менее 20 и
не более 30. Пусть m=число
бракованных изделий. Каждое испытание
– это рассмотрение одного изделия,
поэтому число испытаний n=500,
р=0,05, q=0,95.
Тогда требуется найти Р(В) =
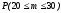 Здесьnpq=5000,050,95=23,75>20.
Можно применять формулу Муавра-Лапласа:
Здесьnpq=5000,050,95=23,75>20.
Можно применять формулу Муавра-Лапласа:
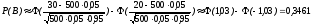
3. Х =число подготовленных вопросов среди трех вопросов экзаменационного билета.. М(Х) 2,001; D(Х) 0,619.
|
Х |
0 |
1 |
2 |
3 |
|
Р |
0,029 |
0,222 |
0,468 |
0,281 |
Вариант 20.
1. вероятность включения сигнала «тревоги» при угоне
0,9998.
2. Вероятность того, что абонент наберет ошибочный телефонный номер, принимается для каждого абонента равной 0,001. Определить вероятность того, что среди 500 произведенных независимо друг от друга вызовов окажется не менее двух ошибочных.
Пусть А= абонент наберет ошибочный телефонный номеПо условию Р(А)=0,001 – это для каждой банки. Поэтому здесь СПИ, при этом можно применять формулу Пуассона, Находим = 5000,001 = 0,5 < 10. Пусть В= среди 500 произведенных независимо друг от друга вызовов окажется не менее двух ошибочных, Рассмотрим противоположное событие , его вероятность равна Р(В)= Р(m=0)+Р(m=1)= 0,6065+0,3033=0,9098. Теперь Р(В)= 1 0,9098=0,0902.
3. Х =число наборов телефонного номера до нахождения нужного номера. М(Х) =1; D(Х)=5/6.
|
Х |
1 |
2 |
3 |
4 |
5 |
6 |
|
Р |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 23.
1. Три спортсмена пытаются выполнить норму мастера спорта. Вероятность того, что первый спортсмен выполнит норму мастера, равна 0,9, второй - 0,7, третий - 0,8. Найти вероятность того, что норма мастера спорта будет выполнена: а) только одним спортсменом; б) хотя бы одним спортсменом.
2. Танк произвел 10 выстрелов по цели; вероятность попадания при каждом выстреле равна 0,4. Найти вероятность того, что число попаданий в цель будет заключено от 4 до 6.
3. Вероятность нарушения герметичности у стеклянной банки с овощными консервами равна 0,0003. Найти вероятность того, что из 10000 банок герметичность нарушена а) у трех банок; б) хотя бы у трех банок.
АлтГУ. Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант24.
1. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,9, во второе - 0,7, в третье - 0,8. Найти вероятность того, что а) только одно отделение получит газеты вовремя; б) хотя бы одно отделение получит газеты с опозданием.
2.Вероятность того, что шахматист в сеансе одновременной игры выиграет партию, равна 0,7. Найти вероятность того, что при игре с 9 партнерами он выиграет: а) 6 партий; б) не менее 5 партий.
3. Вероятность изготовления бракованной отливки равна 0,002. Определить вероятность того, что из 200 отливок количество бракованных составит: а) 2; б) более 3.
АлтГУ. Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 25
риятий, которые выдадут дивиденды с вероятностями 0,6 и 0,75 соответственно. Какова вероятность того, что клиент получит дивиденды:
а) только на втором предприятии; б) хотя бы на одном предприятии?
2. Вероятность того, что в наудачу взятой семье есть дети, равна 0,8. Отобрано случайно 6 семей. Найти вероятность того, что среди этих семей детей имеют: а) 4 семьи; б) хотя бы одна семья.
3. В отделе технического контроля проверяют 480 шестеренок. Вероятность бракованной шестеренки равна 0,1. Найти вероятность того, что число бракованных шестеренок не меньше 40 и не более 56.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 26.
1. В ящике 50 лампочек мощностью 100Вт и 30 лампочек мощностью 40Вт. Найти вероятность того, что среди трех взятых наугад лампочек: а) все одной мощности; б) не более двух лампочек мощностью 100 Вт.
2. Вероятность выигрыша по одному билету денежно-вещевой лотереи составляет 0,2. Найти вероятность того, что из 6 купленных покупателем билетов выигрышными окажутся не менее 2.
3. Известно, что случайная величина Х, принимающая два значения х1 = 1 и х2 = 2, имеет математическое ожидание, равное 7/6.Найти вероятности, с которыми случайная величина Х принимает свои значения. Составить закон распределения случайной величина Х и найти ее дисперсию.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 27.
1. В цехе три участка. Вероятность невыполнения плана первым участком составляет 0,02, для второго - равна 0,05, и для третьего - 0,01. Найти вероятность того, что к моменту подведения итогов работы плановое задание: а) будет выполнено всеми участками; б) не выполнит один участок.
2. Вероятность того, что часы, сданные в ремонт, будут отремонтированы в срок, равна 0,9. Определить вероятность того, что из восьми сданных в ремонт часов более шести будут отремонтированы в срок.
3. Студент в поисках нужной книги обходит библиотеки, в которых он записан. Вероятность наличия книги в каждой из этих библиотек равна соответственно 0,7; 0,5; 0,8. Составить закон распределения числа библиотек , которые посетит студент, Найти математическое ожидание и дисперсию этой случайной величины, а также построить функцию ее распределения.
АлтГУ. Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 28.
1.Среди 10 поступивших в ремонт часов 4 требуют замены маятника. Найти вероятность того, что среди взятых одновременно 3 часов: а) во всех трех требуется замена маятника; б) хотя бы в одних часах требуется замена маятника.
2. Вероятность того, что изготовленная пара обуви высшего качества, равна 0,6.Найти вероятность того, что среди 8 взятых наудачу пар обуви окажутся высшего качества: а) 4 пары; б) не менее 5 пар.
3. В автопробеге участвуют три автомобиля. Вероятность сойти с маршрута для первого автомобиля равна 0,16, для второго - 0,05 и для третьего - 0,1. Составить закон распределения числа машин, недошедших до финиша. Найти математическое ожидание и дисперсию этой случайной величины.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 29.
1. Среди изготовленных 20 пар обуви, 16 - первого сорта, а остальные - второго. Найти вероятность того, что среди взятых наудачу одновременно из этой партии трех пар обуви одна будет второго сорта.
2. Вероятность попадания в мишень при каждом выстреле равна 0,7. Производится 5 выстрелов. Определить вероятность того, что будет не менее 2 попаданий.
3. Брак в цехе составляет 5%.Составить закон распределения числа годных изделий среди наудачу 4 взятых. Найти математическое ожидание и дисперсию этой случайной величины, построить ее функцию распределения.
Алтайский государственный университет. Химический факультет
Самостоятельная работа №1 по курсу теория вероятностей
Вариант 30.
1. В группе из 25 студентов экзаменационную сессию на "хорошо" и "отлично" сдали 10 студентов. Определить вероятность того, что из двух наудачу вызванных студентов этой группы экзаменационную сессию на "хорошо" и "отлично" сдали: а) оба студента; б) только один студент; в) хотя бы один студент.
2. Вероятность того, что автобус сломается в течение рабочего дня , равна 0,1. Найти вероятность того, что из 6 автобусов на линии сломаются не более 4.
3. Из орудия ведется стрельба по удаляющейся цели до первого попадания. Вероятность попадания при первом выстреле 0,6, при каждом следующем уменьшается на 0,1. Составить закон распределения числа промахов при имеющихся 4 снарядах. Найти математическое ожидание и дисперсию этой случайной величины.
ОТВЕТЫ к контр. работе по теор. вер.
1.
1).р1=0,06;
р2=0,84.
2). р1=0,99;
р2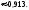 .
3).
.
3).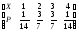 ;
М(Х)=2,5;D(X)=
;
М(Х)=2,5;D(X)=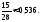
2.
1).
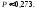 .
2).
.
2).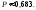 .
3).
.
3). ;
М(Х)=2,02;D(X)
;
М(Х)=2,02;D(X)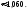
3.
1). Р1=0,092;
Р2=0,994.
2).
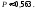 3).
3).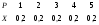 ;
М(Х)=3;D(X)=2.
;
М(Х)=3;D(X)=2.
4.
1).р1=0,06;
р2=0,495.
2).
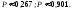 3).
3). ;
М(Х)=2;D(X)=69.
;
М(Х)=2;D(X)=69.
5.
1).р1=0,3;
р2=0,9.
2).
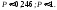 3).
3).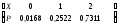 ;
М(Х)
;
М(Х)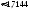 ;D(X)
;D(X)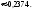 .
.
6.
1).
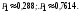 .
2).
.
2).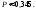 3).
3).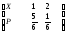 ;D(X)=
;D(X)=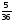 .
.
7.
1).
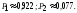 .
2).
.
2).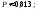 3).
3).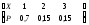 ;
М(Х)=1,45;D(X)=0,5475.
;
М(Х)=1,45;D(X)=0,5475.
8.
1).
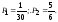 .
2).
.
2).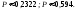 3).
3). ;
М(Х)=0,31;D(X)=0,2719.
;
М(Х)=0,31;D(X)=0,2719.
9.
1).
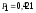 .
2).
.
2).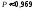 3).
3).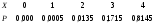 ;
М(Х)=3,8;D(X)=0,19.
;
М(Х)=3,8;D(X)=0,19.
10.
1).
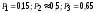 .
2).
.
2).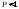 .
3).
.
3).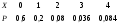 ;
М(Х)=0,804;D(X)=1,5416.
;
М(Х)=0,804;D(X)=1,5416.
11.
1).
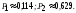 .
2). 3).
.
2). 3).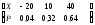 ;
М(Х)=28;D(X)=273,6.
;
М(Х)=28;D(X)=273,6.
12.
1).
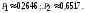 .
2). 3).
.
2). 3). ;
М(Х)=0,2;D(X)=0,185.
;
М(Х)=0,2;D(X)=0,185.
13.
1).
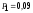 .
2). 3).
.
2). 3). ;
М(Х)
;
М(Х)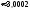 ;D(X)
;D(X)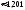 .
.
14.
1).
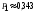 .
2). 3).
.
2). 3).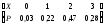 ;
М(Х)=2,05;D(X)=0,4175.
;
М(Х)=2,05;D(X)=0,4175.
15.
1).
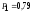 .
2). 3).
.
2). 3).
 ;
М(Х)=2,5;D(X)=1,25.
;
М(Х)=2,5;D(X)=1,25.
16.
1).
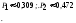 .
2). 3).
.
2). 3).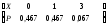 ;
М(Х)
;
М(Х)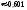 ;D(X)
;D(X)
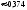 .
.
17.
1).
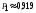 .
2). 3).
.
2). 3).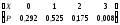 ;
М(Х)=0,899;D(X)
;
М(Х)=0,899;D(X)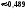 .
.
18.
1).Р=0,9. 2). 3).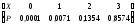 ;
М(Х)=2,8501;D(X)
;
М(Х)=2,8501;D(X)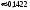 .
.
19.
1).
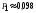 .
2). 3).
.
2). 3). ;
М(Х)=2;D(X)=0,6208.
;
М(Х)=2;D(X)=0,6208.
20.
1).
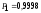 .
2). 3).
.
2). 3).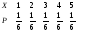 ;
М(Х)=2,5;D(X)
;
М(Х)=2,5;D(X)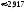 .
.
21.
1).
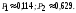 .
2). 3).
.
2). 3).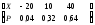 ;
М(Х)=28;D(X)=273,6.
;
М(Х)=28;D(X)=273,6.
22.
1).
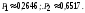 .
2). 3).
.
2). 3). ;
М(Х)=0,2;D(X)=0,185.
;
М(Х)=0,2;D(X)=0,185.
23.
1).
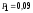 .
2). 3).
.
2). 3). ;
М(Х)
;
М(Х)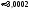 ;D(X)
;D(X) .
.
24.
1).
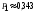 .
2). 3).
.
2). 3).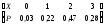 ;
М(Х)=2,05;D(X)=0,4175.
;
М(Х)=2,05;D(X)=0,4175.
25.
1).
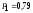 .
2). 3).
.
2). 3).
 ;
М(Х)=2,5;D(X)=1,25.
;
М(Х)=2,5;D(X)=1,25.
26.
1).
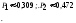 .
2). 3).
.
2). 3).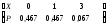 ;
М(Х)
;
М(Х)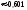 ;D(X)
;D(X)
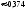 .
.
7.Экзаменационные вопросы и билеты
