Переход от дифференциального уравнения порядка nк системе изn-дифференциальных уравнений 1-го порядка

Такой переход позволяет единообразно исследовать системы любого порядка, что имеет важное значение, например, при моделировании на ЭВМ, в этом случае проще использовать стандартные матричные операции, чем иметь дело с дифференциальными уравнениями разных порядков.

Вводим дополнительные переменные (x₁……x_n), равные производным y(t):

Перепишем уравнение (5): y⁽ⁿ⁾= -1/a₀ (a₁y^(n-1) +…+a_ny - b₀u^(m) -…-b_mu).

Очевидно, что имеет место следующая система из n уравнений:

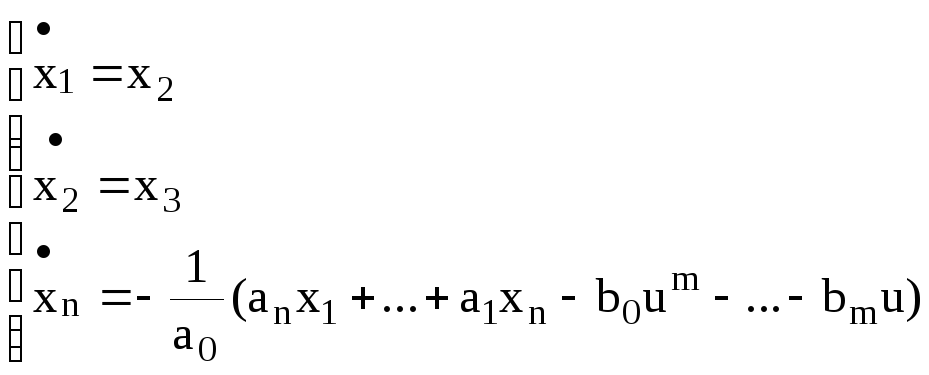
Начальные условия для y(t) переходят в начальные условия для (x₁……x_n).

Для выражения выходной величины преобразуем (6) в векторно-матричную

систему с выходом. Отметим для этого, что настоящий выход объекта y(t) равен х₁. Можно ввести вектор-строку из n компонент: с=(1 0 0 0 …0), при этом х₁= с^т (х₁ …….х _n)= 1х₁+0х ₂ + …….+0х _n.

Теперь система дифференциальных уравнений (6) может быть записана в матричном виде следующим образом:

Здесь обозначено: ;

Решение системы уравнений (7) всегда может быть записано в следующем виде (Формула Коши, интеграл Дюамеля):

Здесь первое слагаемое – общее решение однородного уравнения, второе – частное неоднородного. Формула (8) справедлива вне зависимости от порядка исходного дифференциального уравнения.

В правую часть уравнения (7) и формулы (8) входят производные от управляющего воздействия. Можно показать, что от этих производных можно избавиться. Они будут вычисляться “автоматически” в процессе решения системы уравнений, и выглядит это следующим образом. Нужно вместо вектора b взять вектор g, компоненты g₁,…,g_n-1 которого уже не обязательно равны 0, но вычисляются по следующей рекуррентной формуле:

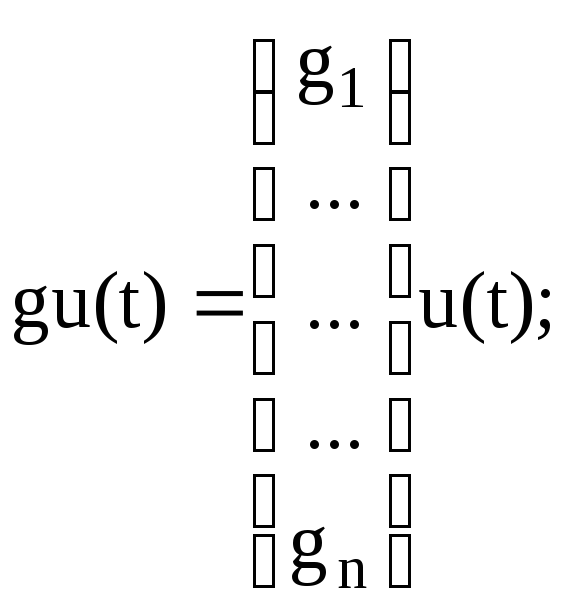
Это рекуррентная формула в том смысле, что g_i вычисляется последовательно, друг за другом. В случае, когда нет производных от входа, автоматически получаем вектор g = (0 0 ….0 b₀/a₀).

Геометрическая интерпретация и пример линеаризации.

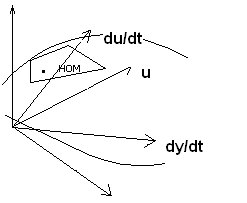
. Это уравнение (**) можно понимать, как уравнение поверхности в многомерном пространстве с многочисленными координатами, являющимися переменными y, u и их производными всех входящих в (**) порядков.

Номинальная траектория есть просто точка на поверхности, линеаризованное уравнение (2-4) – уравнение касательной плоскости в номинальной точке.

Пример 2. Линеаризация водоема с карасями.

; - Полученное ранее в лекции 2 уравнение, описывающее количество рыбы в водоёме.

Определим номинальный режим (траекторию). Часто номинальная траектория находится из условия равновесия.

, при с =3/16 получаем

z₁= 0.25; z₂ = 0.75.

В окрестности z₁ движение неустойчиво (численность нестабильна), а z₂ =0.75 подходит для номинального режима. Проведём линеаризацию именно в окрестности z₂.

Таким образом:

В нашем случае нелинейность выражена только в виде зависимости от z.

Переходя к исходному уравнению и вводя переменные в отклонениях:x=z-z_ном, u=c-c_ном, получаем линейное д.у. в отклонениях от номинального режима:

Рассмотренные статические характеристики полностью характеризуют поведение элементов автоматики, установившихся режимов, однако в автоматических- системах элементы автоматики работают в неустановившихся, переходных режимах, это связано с тем, что внешние силы, действующие на САУ непрерывно и случайно изменяются, что приводит к непрерывному изменению входной и выходной величины каждого элемента системы.

Переходным процессом системы называется изменение во времени ее состояния параметров с момента появления управляющего или возмущающего воздействия на систему, находившуюся в установившемся (равновесном) состоянии до момента установления в ней вновь установившегося состояния.

Чаще рассмотрение переходных режимов элементов автоматики приводит к дифференциальным уравнениям того или иного вида, в результате физическая задача определения выходной величины элемента системы автоматики при изменяющемся входном сигнале сводится к математической задаче составления дифференциального уравнения и отыскании его решения.

Пусть имеется звено системы автоматического управления.

X – входная величина

Y –выходная величина

и- возмущающие воздействия, влияющие на выходную величину.

Пусть дифференциальное уравнение, описывающее динамику этого элемента, имеет вид :

F()=0 (1)

Неизвестной величиной является y, для решения этого уравнения должны быть заданы x, ,и начальные условия.

y=y₀

x=x₀

=₀

=₀

(1) перепишем в виде:

F()=0 (2)

Уравнение статической характеристики звена в неявном виде.

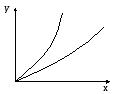
Решая уравнение (2) относительно y и x получим уравнение в явном виде:

Семейство

статических

характеристик

Все это линейные уравнения.

При исследовании нелинейных элементов САУ описываемых нелинейными уравнениями САУ, такие уравнения пытаются линеаризовать, т.е. заменить нелинейное уравнение линейным, решение которого достаточно близко к решению исходного нелинейного уравнения. Для линеаризации дифференциальных уравнений ТАУ используется метод малых отклонений, суть его в том, что если при изменении входной величины звена, изменение выходной величины является непрерывной функцией времени и отклонение всех изменяющихся величин от их установившихся значений малы, то можно допустить линеаризацию нелинейных зависимостей, при этом за начало отсчета координат берут параметры равновесного состояния систем, а сами уравнения для элементов и систем составляют в отклонениях от состояния равновесия (приращения), таким образом, в уравнение входят не абсолютные значения величин, а их отклонения от заданных равновесных значений.

При отклонении температуры от заданного значения, регулирующий орган воздействует на исполнительный, который регулирует количество газа в печь и устанавливает необходимую температуру. Рабочая характеристика Q=f(S) является нелинейной.

В равновесном состоянии заданное значение температуры обеспечивается подачей в печь газа в количестве Q₀ при степени открытия заслонки S₀ . При появлении возмущающих воздействий заданное значение температуры восстанавливается путем изменения подачи газа на при дополнительном перемещении заслонки на.

Вход заслонки – S, регулирующий количество газа.

Q –количество газа.

Учитывая малость отклонений можно в окрестностях точки 0₁, соответствующую равновесному состоянию, заменить участок кривой Q=f(S) прямой, касательной к этой кривой 0, при этой замене получаем линейную зависимость между входом заслонки и расходом газа около равновесного состояния в виде:

Q= (*)

Путем переноса начала координат в точку 0₁, получаем уравнение, определяющее линейную зависимость между дополнительным входом заслонки и дополнительной подачей газав отклонениях.

(**)

-дифференциальная чувствительность, постоянен в окрестностях точки 0₁, при удалении от нее погрешность возрастает, тем быстрее, чем больше кривизна нелинейной зависимости.

Аналитическая линеаризация выполняется путем разложения функции Q=f(S) в ряд Тейлора для точки равновесного состояния системы.

И исключение из ряда членов высших порядков малости, достаточная точность достигается при отбрасывании членов разложения со степенями больше первой.

f(x)=f(x₀)=f’(x₀)

-представляет линеаризованную функцию f(x) , представленную в отклонениях от равновесного состояния.

f’(x₀)-производная этой функции в точке равновесного состояния, равная тангенсу наклона линеаризованного участка в окрестностях этой точки.

Вопросы самоконтроля:

1. Дать определение переходного процесса системы.

2. Дать определение линеаризации статических характеристик систем управления.

3. Дать определение статическим и астатическим звеньям систем управления.

4. Дать определение статическим характеристикам звеньев: линейным и нелинейным.

Список литературы по теме лекции:

1. Бесекерский В.А., Попов Е.П. Теория CAP, М.,2005

2. Иващенко Н.Н. Автоматическое регулирование, М.,2003