Учебный материал Понятие решетчатой и модулированной функций. Дискретное преобразование Лапласа

Математическим аппаратом для исследования импульсных систем является дискретное преобразование Лапласа. Непрерывная функциональная зависимость может быть представлена решетчатой функцией х[mT], которая состоит из ординат. Модулированный сигнал (последовательность -функций модулированная ординатами входного с-функций, модулированная ординатами входного сигнала в дискретные моменты времени).

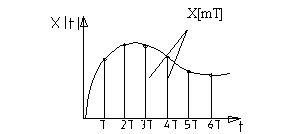
Рис.1 Рис.2

Из рис.2 в моменты времени, не равные mT, решетчатая функция =0. В общем случае одна и таже решетчатая функция может соответствовать различным непрерывным и разрывным функциям, если только их ординаты в дискретные моменты времени t=mT равны значениям решетчатой функции. Т.о. решетчатая функция не может полностью отразить свойства непрерывной функции, которую она представляет, поэтому обычно используют понятие смещенной решетчатой функции, в которой t=mT₀f, т.е. когда дискретные значения функции выбираются для смещенных на относительноmT моментов времени. Если параметр непрерывно изменять от 0 до Т, то решетчатая функция становится тождественной определенной непрерывной функции.

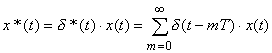
Сигнал x^*(t) -реально существующий сигнал;

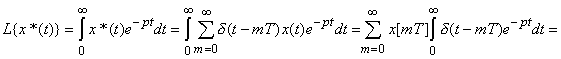
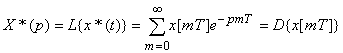
D-дискретное преобразование Лапласа.

Дифференцирование и интегрирование решетчатых функций

Аналогом первой производной для решетчатой функции является либо первая прямая разность:

 f [n] = f [n+1] - f [n],

либо первая обратная разность:

 f [n] = f [n] - f [n-1].

Аналогов второй являются вторые разности. Прямая:

² f [n] =f [n+1] -  f [n] = (f [n+2] - f [n+1]) - (f [n+1] - f [n]) = f [n+2] - 2 f [n+1] + f [n],

и обратная:

² f [n] =  f [n] -f [n-1] = f [n] - 2 f [n-1] + f [n-2].

По аналогии могут определяться и высшие разности:

k f [n] = v=0k (-1)vCkvf [n+k-v]

k f [n] = v=0k (-1)vCkvf [n-v]

где: C_k^v = k! / (v!(k-v)!).

Очевидно, что если f [n] определена только для положительных n, то для n=0 все обратные разности ^k f [n] равны нулю, что позволяет ...

Аналогом интеграла является неполная сумма:

 [n] = _m=0^n-1 f [m] = м₌₁ⁿ f [n-v],

и полная сумма:

_o[n] =  [n] + f [n].

Вопросы самоконтроля:

1. Как используется преобразование по Лапласу для исследования импульсных систем?

2. Дайте определение решетчатых функций.

Лекция 52

Цель лекции: изучение методов исследования устойчивости импульсных систем.

Задачи лекции:

1. Аналитическое обоснование получения разностного уравнения импульсной системы.

2. Критерий устойчивости импульсной системы.

3. Биполярные преобразования импульсных систем.

Желаемый результат:

Студенты должны знать:

1. Математический аппарат получения разностного уравнения импульсной системы;

2. Порядок определения устойчивости импульсной системы;

3. Порядок проведения биполярных преобразований импульсных систем.

Учебный материал Исследование устойчивости системы по разностному уравнению

Аналогом ДУ для импульсной системы является уравнение в конечных разностях или разностное уравнение (РУ):

b₀^my[n] + b₁^m-1y[n] + ... + b_m y[n] = f [n],

(оно может быть составлено и в прямых разностях). Если раскрыть разности, то уравнение будет иметь вид:

a₀ y[n] + a₁ y[n-1] + ... + a_m y[n-m] = f [n],

где:

am-k = v=0k (-1)m-k bv Cm-vk-v ;

Cm-vk-v = (m-v)! / [ (k-v)! (m-k)! ] .

РУ легко машинизируются и для их расчета можно составлять рекуррентный алгоритм.

Учтем запаздывание передаточной функцией звена чистого запаздывания и вынесем теперь уже изображение дискретной последовательности y[n] в уравнении (1) за скобку:

(a₀ + a₁e^-Ts + ... + a_me^-mTs) Y ^*[s] = F ^*[s],

введем обозначение z = e^Ts и перепишем уравнение:

(a₀ + a₁ z ^-1 + ... + a_m z ^-m) Y [z] = F [z].

Решая для него ХУ (левая часть приравненная к нулю) можно получить "Общее решение" - т.е. переходную составляющую:

y [n] = С₁ z₁ⁿ + С₂ z₂ⁿ + ... +  С_m z_mⁿ ,

где: z₁, z₂, ..., z_m - корни ХУ; а C_i - произвольные постоянные.

Вид решения ХУ определяет условие устойчивости для систем, описанных с помощью РУ:

| z_i | < 1.