
- •Свойства систем автоматического управления
- •Структурная устойчивость (неустойчивость)
- •Запас устойчивости
- •Область устойчивости
- •Метод д-разбиения
- •Оценка качества регулирования
- •Показатели качества переходной характеристики
- •Точность в установившихся режимах
- •Интегральные оценки качества
- •Оценка качества переходного процесса по расположению нулей и полюсов передаточной функции
- •Влияние расположения нулей и полюсов на переходную характеристику
Свойства систем автоматического управления
Рассмотренная выше устойчивость (совместно с критериями ее определения) не является единственным свойством систем автоматического управления. Системы характеризуются: запасом устойчивости, областями устойчивости, притяжения, качеством регулирования и другими характеристиками. Рассмотрим некоторые из них.
Структурная устойчивость (неустойчивость)
Это такое свойство замкнутой системы, при наличии которого она не может быть сделана устойчивой ни при каких изменениях параметров.
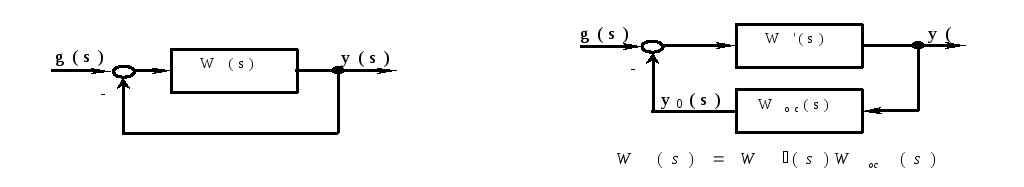
Пусть
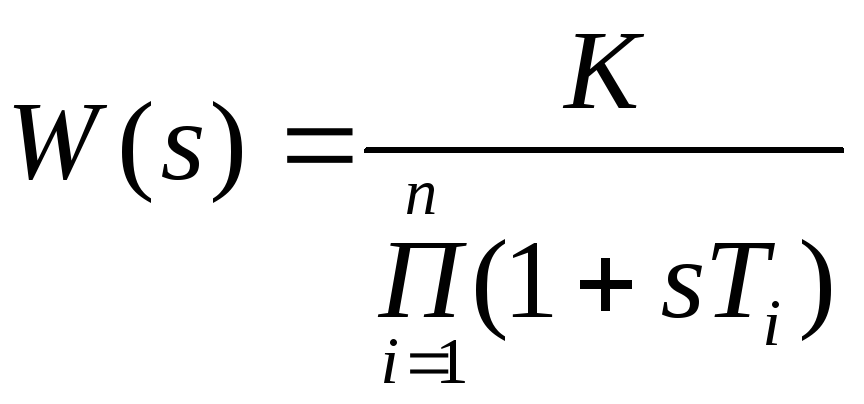 .
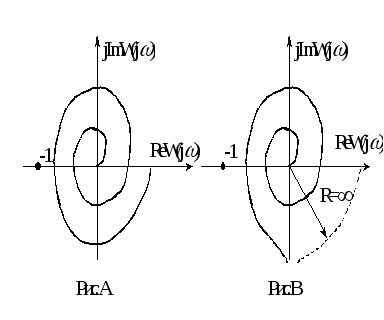
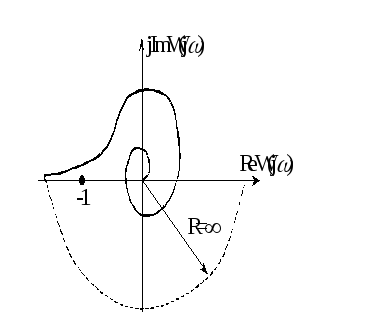
Годограф Найквиста для данной
системы изображен на Рис.А. Устойчивость
этой системы определяется значениями
параметров
.
Годограф Найквиста для данной
системы изображен на Рис.А. Устойчивость
этой системы определяется значениями
параметров
![]() и
и![]() .
Рассматриваемая система является
структурно устойчивой.
.
Рассматриваемая система является
структурно устойчивой.
Пусть
![]()
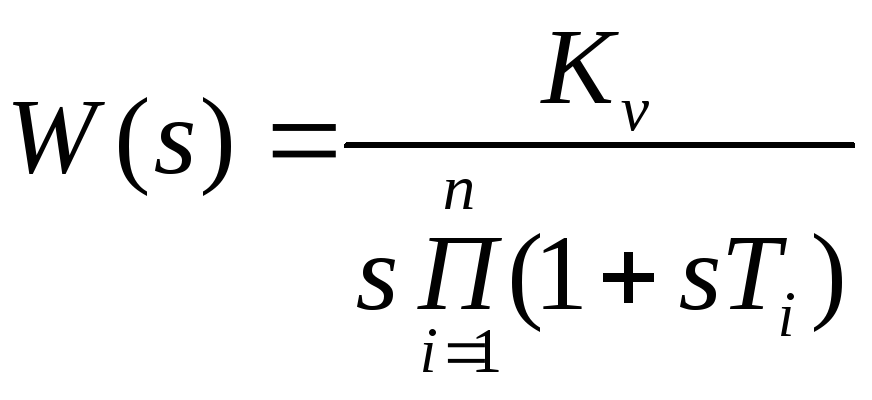 .
(Рис.В). Устойчивость также зависит
от параметров
.
(Рис.В). Устойчивость также зависит
от параметров
![]() и
и![]() .
Система структурно устойчива.
.
Система структурно устойчива.
Пусть
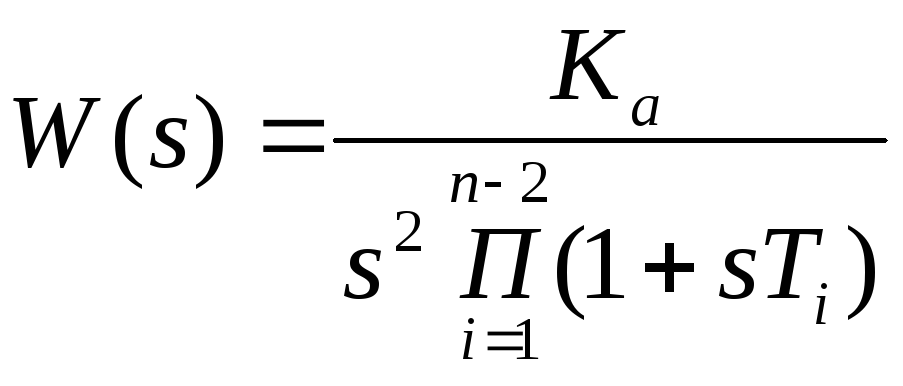 .
В любом случае (при любых значениях
параметров) система будет неустойчива.
То есть система является структурно
неустойчивой.
.
В любом случае (при любых значениях
параметров) система будет неустойчива.
То есть система является структурно
неустойчивой.
В частном случае передаточная функция
имеет вид
![]() .
При этом соответствующее
характеристическое уравнение замкнутой
системы:
.
При этом соответствующее
характеристическое уравнение замкнутой
системы:
![]() .
Нарушен принцип перемежаемости
корней и полюсов. Система неустойчива.
Структурно неустойчива.
.
Нарушен принцип перемежаемости
корней и полюсов. Система неустойчива.
Структурно неустойчива.
Система с передаточной функцией
![]() - структурно неустойчива, так как для
замкнутой системы
- структурно неустойчива, так как для
замкнутой системы![]() ,
при этом коэффициенты
,
при этом коэффициенты![]() ,
,![]() ,
,![]() ,
,![]() ,
- все положительны, но из условия
,
- все положительны, но из условия![]() следует, что
следует, что![]() ,
откуда
,
откуда![]() ,
или
,
или![]() .
То есть система неустойчива.
.
То есть система неустойчива.
Система
![]() также структурно устойчива. Здесь звено
также структурно устойчива. Здесь звено![]() - квазиапериодическое (статически
неустойчиво). Характеристическое
уравнение замкнутой системы
- квазиапериодическое (статически
неустойчиво). Характеристическое
уравнение замкнутой системы![]() .
Откуда можно получить два граничных
условия:
.
Откуда можно получить два граничных
условия:![]() и
и![]() .
.
Для одноконтурных систем имеют место условия (Мейеров М.В.):
Пусть одноконтурная система состоит из:
![]() -
интегрирующих звеньев,
-
интегрирующих звеньев,
![]() -
неустойчивых звеньев,
-
неустойчивых звеньев,
![]() -
консервативных звеньев. Тогда при
отсутствии в системе дифференцирующих
звеньев она будет структурно устойчива
в том случае, если
-
консервативных звеньев. Тогда при
отсутствии в системе дифференцирующих
звеньев она будет структурно устойчива
в том случае, если![]()
![]()
В случае многоконтурных систем соотношения Мейерова необходимо применять к каждому контуру, входящему в систему.
Запас устойчивости
Факт обнаружения устойчивости не дает уверенности в работоспособности системы.
Возможны неточности (погрешности), так как:
математическое описании системы идеализировано;
часто бывает произведена линеаризация звеньев;
неточность определения параметров;
изменение условий работы (по отношению к моделируемым).
Следовательно, необходим запас устойчивости.
При использовании критерия Гурвица запас определяется величиной предпоследнего минора:
Если
![]() - запас устойчивости отсутствует;
- запас устойчивости отсутствует;![]() -
запас имеется.
-
запас имеется.
Запас устойчивости в системе характеризует степень устойчивости.
Запас устойчивости и степень устойчивости можно определить по расположению корней характеристического уравнения и по частотных характеристикам системы.
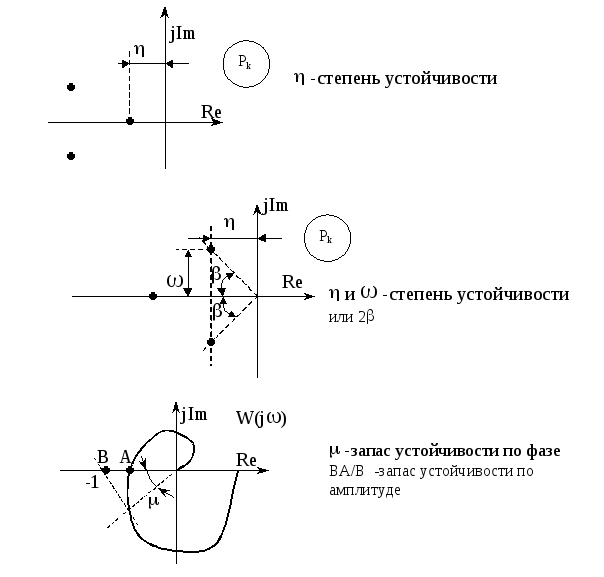
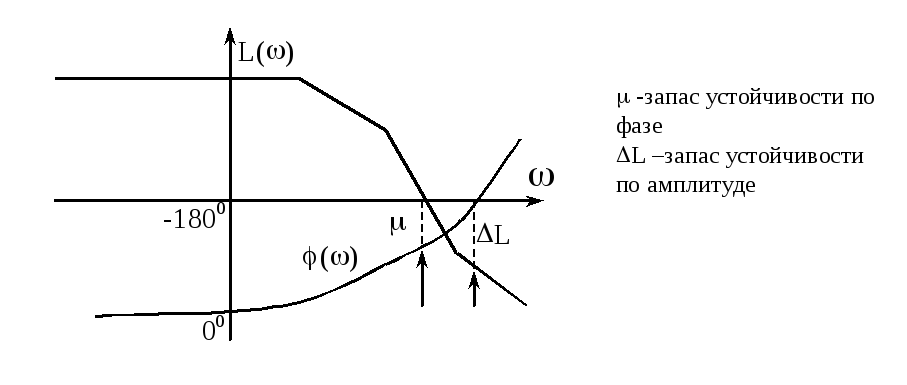
Аналогично можно определить запас устойчивости по логарифмическим характеристикам L() и(),применяемым при определении устойчивости по критерию Найквиста.
Область устойчивости
На практике проектировщиков систем автоматического управления интересует пространство (область, пределы, диапазон) параметров, при которых системы является устойчивой. Множество значений параметров, при которых система обладает свойством устойчивости, называется областью устойчивостисистемы.
Для определения областей устойчивости имеется несколько методик.
На основе алгебраического критерия устойчивости Гурвица;
Метод Д-разбиения;
Метод корневого годографа.
Область устойчивости по Гурвицуопределяется с помощью использования
равенств в условиях Гурвица вместо
неравенств. Чаще всего определение
границы искомой области может быть
произведено при условии![]() .
(Смотри пункт "Определение критического
коэффициента усиления"). Отсюда
определяется зависимость интересующего
нас параметра
.
(Смотри пункт "Определение критического
коэффициента усиления"). Отсюда
определяется зависимость интересующего
нас параметра![]() от
параметра.
Получаемая зависимость()-
граница области устойчивости системы.
от
параметра.
Получаемая зависимость()-
граница области устойчивости системы.
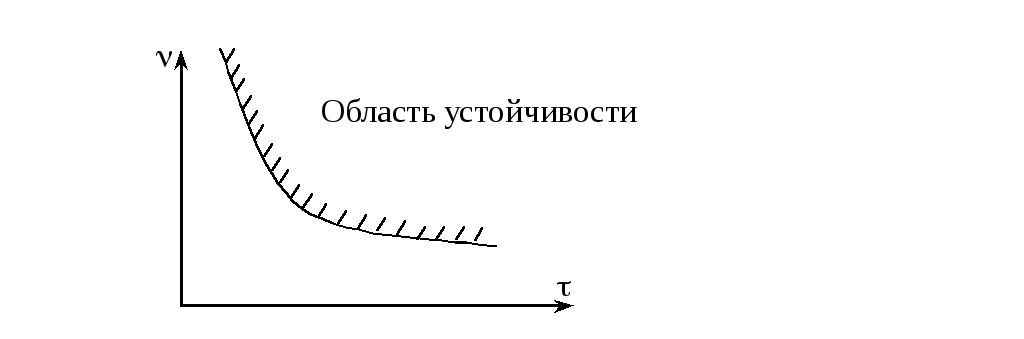
В системах более высоких порядков возникает необходимость рассмотрения других миноров. При этом область устойчивости может сужаться.
