Лекция 41

Цель лекции: изучение метода изоклин; изучение метода припасовывания.

Задачи лекции:

1. Метод изоклин.

2. Метод припасовывания.

Желаемый результат:

Студенты должны знать:

1. Порядок использования для исследования нелинейных систем метода изоклин;

2. Порядок использования для исследования нелинейных систем метода припасовывания.

Учебный материал Метод изоклин

Пусть для нелинейной системы получено дифференциальное уравнение вида:

(1),

где - управляемая координата системы;-известные нелинейные функции.

Понизим порядок уравнения с помощью подстановки:

(2), тогда (3).

С учетом (2) и (3), (1) запишется в виде :

(4).

У равнения (2) и (4) объединим в систему:

(5)

Разделим а) на б) в системе (5):

(6).

Если заданные функции достаточно просты, то уравнение (6) допускает интегрирование, в результате которого находится решение уравнения (6) в виде:

(7) – фазовая линия на плоскости .

Однако, при сложных интегрирование (6) невозможно или затруднительно. В этих случаях фазовую траекторию (7) строят обходным приемом. В уравнение (6) положим:

(8).

Геометрически - касательная к фазовой траектории (7) в тех точках, в которых угловой коэффициент.

С учетом (8), уравнение (6) запишется в виде:

(9) – алгебраическое уравнение.

Задавая в (9) для переменной дискретный набор значенийможно вычислить дискретный набор значений. Каждая пара координатопределяет точку на фазовой плоскости. Совокупность точек определяют линию, которая называется изоклиной. В каждой точке этой линии угловой коэффициент касательной к фазовой траектории остается постоянным.

На изоклину на равных расстояниях наносятся короткие параллельные отрезки, угловой коэффициент наклона которых .

Постоянная выбрана произвольной, для нее можно выбрать целый набор значений. Для каждого значения по уравнению(9) можно построить свою изоклину. В итоге получаем семейство изоклин. Семейство изоклин позволяет восстановить по ним фазовую траекторию системы.

В целом этот метод является приближенным, но дает достаточный результат для практического применения.

Метод припасовывания (сшивания).

Метод изоклин позволяет построить портрет приблизительно. В ряде задач, для анализа в СУ необходимо иметь точный фазовый портрет, построенный на основе аналитических выражений. Общих методов такого построения нет, они найдены только для некоторых частных случаев построения СУ.

Пусть исходная анализируемая СУ сведена к структурной схеме (рис.1):

F(u-x)

W_л(р)

u u-x x₁ x

рис.1

x

Где - передаточная функция линейной части системы;

- статическая характеристика нелинейной части системы.

По определению передаточной функции: (1).

Для определенности зададим линейную часть в виде (2),

тогда (3).

Будем считать, что на вход системы подано постоянное воздействие . Тогда перейдем в системе от самих величин к их отклонениям относительно постоянного входного воздействия. Обозначим отклонение(4). Дифференцируя (4), получим

(5), (6).

С учетом (5) и (6), уравнение (3) запишется в виде:

(7),

(8).

Уравнения (8) и (6) объединяем в систему:

(а)

(б) ⁽⁹⁾

Деля (а) на (б), получим:

(10).

Решение уравнения (10) можно найти только при конкретном задании нелинейной функции.

1) Пусть в качестве нелинейного элемента в анализируемую систему включено идеальное двухпозиционное реле со статической характеристикой (11) (рис.2):

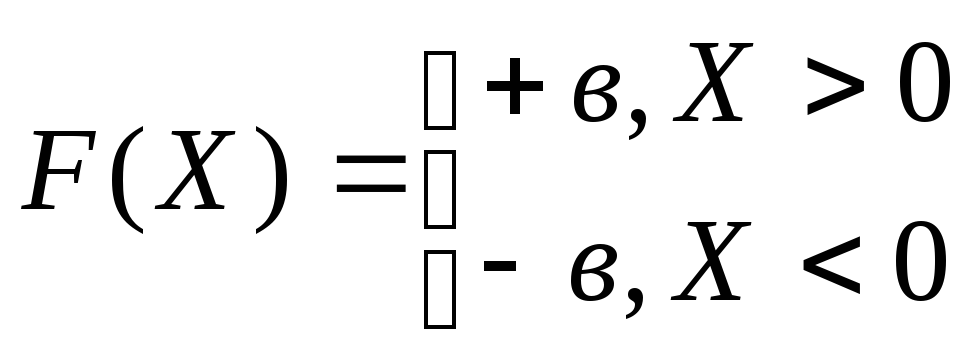(11)

рис.2

Статическая характеристика симметрична относительно начала координат- нечетная функция, тогда. В результате получим:

(12).

С учетом (11) нелинейное уравнение (12) эквивалентно системе линейных уравнений:

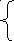(а)

(б) ⁽¹³⁾

Решение каждого уравнения найдем в отдельности:

Пусть для уравнения (а) в начальный момент системы выведена в т.с координатами. Проинтегрируем уравнение (13а) в границах отдои отдо.

;

;

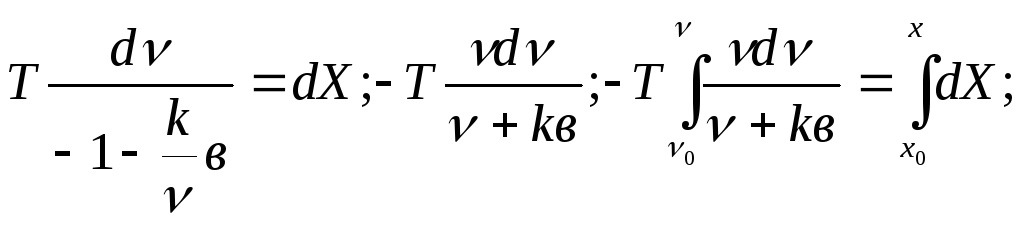
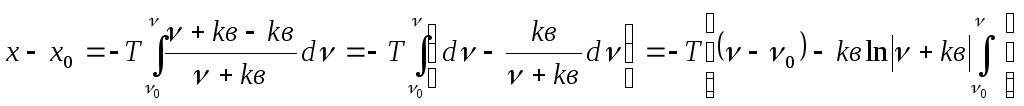(14), при .

Решение (14) есть искомый участок фазовой траектории . Аналогичным образом ищется решение уравнения (13б). Отличие только в том, что в найденном решении (14) значениезаменяется на. Тогда :

(15), при .

Предположим, что начальная т.соответствует левой полуплоскости, т.е.и тогда работает уравнение (15). Задавая в уравнении дискретный набор значений для, вычислим дискретный набор для. Полученные наборы координатопределяют на базовой плоскости наборы точек, соответствующих фазовой траектории. Типовой вид кривой показан на рис.3:

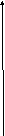
При переходе фазовой траектории через точку , начинает работать уравнение (14). Аналогичным образом, задавая в (14) набор значений, можно получить набор соответствующих. По полученным точкам строится второй участок фазовой траектории. В т.сшиваются решения по уравнениям (14) и (15). Координаты т.являются конечными значениями. Иначе, значения- «пас» от одного уравнения к другому (метод припасовывания). Все т.,,,… лежат на одной прямой; в этих точках происходит переключение с одного уравнения на другое. По этой причине линия называется линией переключения. В данном случае линия переключения совпадает с вертикальной осью. Характер фазовой линии таков, что она постоянно приближается к началу координат (это значит, что анализируемая система с релейным элементом устройства). При движении к состоянию устойчивости амплитуда колебания постоянно уменьшается, а частота переключения растет. Формально, в т.О амплитуда переключений стремится к 0, а частота.

2) Пусть в качестве нелинейного элемента в анализируемой системе используется реле с гистерезисом со статической характеристикой:

рис.4

(19)

С учетом (19) нелинейное уравнение (10) распадается на эквивалентную систему двух линейных уравнений:

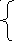
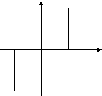
Полученная система в точности совпадает системой для идеального двухпозиционного реле (1-ый случай). Отличие в том, что переключение с одного уравнения на другое будит происходить не в точке , а в точке, прии в точке, при. На фазовой плоскостиприведенным условиям соответствуют линии переключенияв верхней полуплоскости ив нижней полуплоскости.

рис.5

Т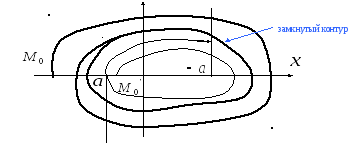ак как решение уравнений в системе (19) найдено выше и линии переключения обозначены на рис.5, фазовый портрет системы будет иметь вид:

Причем, при первоначальном смещении изображающей точки системы в т.фазовая линия приближается к началу координат. Если систему вывести первоначально в т., то фазовая траектория удалится от начала координат,обе фазовых линии должны попадать на замкнутый контур (предельный цикл). Замкнутый контур соответствует режиму автоколебаний в системе.

Подобным образом можно анализировать системы с другими нелинейными элементами. Если статическая характеристика нелинейного элемента имеет произвольный характер, то ее можно заменить аппроксимирующей ломаной линией в форме прямоугольных ступенек. В этом случае, нелинейные уравнения системы сводятся к системе линейных уравнений, число которых равно числу ступенек. Линии переключения в общем случае также могут быть не прямыми линиями, а кривыми.

Вопросы самоконтроля:

1. Опишите правила построения фазового портрета методом изоклин.

2. Опишите правила построения фазового портрета методом припасовывания.

3. Дайте определение замкнутого контура фазового портрета.

4. Дайте определение линиям переключения.

5. Охарактеризуйте состояние нелинейной системы по фазовому портрету.