Определение параметров системы (регулятора) по заданной степени колебательности.

Задача выбора параметров заданной системы из условия заданной степени колебательности аналогична задаче об устойчивости. И в том, и в другом случае накладываются ограничения на область расположения корней характеристического уравнения. Различие заключается лишь в конфигурации областей (левая полуплоскость – устойчивость; сектор АОВ на рис. 4 – степень колебательности). Для определения параметров системы из условия m  m_зад. может быть использован метод смещенного уравнения.

Метод смещенного уравнения.

Пусть характеристическое уравнение замкнутой системы имеет вид

a

(14)

_n sⁿ + a _n-1 s^n-1 +... + a₁s +a ₀ = 0.

Повернем оси координат плоскости S на угол  = arctg m _зад. против часовой стрелки (рис. 5) и введем новую переменную .

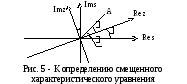
Запишем координаты точки А (рис.5) относительно новых и старых осей координат:



(15)

=s =

Так как , то из (15) следует

s = A₁ ^. = A₁ = А₁

Отсюда находим связь между координатами s и z

s

(16)

=

Подставляя s = в характеристическое уравнение замкнутой системы, получим

a

(17)

_n^.e^jn zⁿ + a_n-1^.e^j(n-1) z^n-1 + … + a₁^.e^j z + a₀ = 0.

и

(18)

ли

A_n^.zⁿ + A_n-1^.z^n-1 + … + A₁^.z + A₀ = 0,

где A_k = a_k^. e^jk.

Уравнение (18) является характеристическим уравнением системы в новых осях координат и называется смещенным характеристическим уравнением.

Отметим, что коэффициенты А _к - комплексные числа. Будем называть систему устойчивой в новых координатах, если ее корни лежат левее новой мнимой оси (необходимо иметь в виду, что при повороте осей расположение корней не изменяется, а изменяются лишь их координаты). Для оценки устойчивости системы может быть использован критерий Михайлова.

Теорема. Если система устойчива в новой системе координат, то ее степень колебательности m  tg  .

Другими словами, все корни характеристического уравнения лежат в заштрихованной области (рис. 6).

Доказательство.

Для действительных корней это очевидно. Пусть теперь один из комплексных корней, например, s₁ (рис. 6) расположен вне заштрихованной области, тогда сопряженный ему корень s₂ будет лежать в области неустойчивости, что противоречит первоначальному предположению. С другой стороны, для комплексно-сопряженных корней, расположенных в заштрихованной области, условие устойчивости всегда выполняется. Таким образом, условие устойчивости системы в новых координатах эквивалентно условию m  tg . Причем знак равенства соответствует границе устойчивости.

Условия устойчивости в новых координатах могут быть использованы для определения параметров системы.

Построение областей равной степени колебательности в плоскости параметров системы

Предположим, что некоторые параметры системы регулирования (например, параметры регулятора) могут изменяться. Найдем область изменения варьируемых параметров, при которых m  m _зад. Решение задачи проведем методом D-разбиения на примере системы, структурная схема которой приведена на рис. 7.

Будем считать, что параметры ПИ-регулятора К₀ и К₁ могут изменяться. Требуется найти область изменения К₀ и К₁, при которых m  m _зад. Передаточная функция разомкнутой системы

W

(19)

_ =

Характеристическое уравнение замкнутой системы имеет вид:

К

(20)

₀ К_y + К₀ К_y + а ₀ s + а ₁ s² + а ₂ s³ = 0

Сделав замену s = z е^{j }, где = arctg m _зад.,

запишем смещенное уравнение

К

(21)

₀ + К₁е ^{j } z + а ₀ е ^{j } + а₁ е ^{j 2 } z² +а ₂ e ^{j 3 } z ³ = 0.

Для выполнения условия m = m _зад., как было показано выше, необходимо, чтобы система находилась на границе устойчивости в новых осях координат. Иными словами, смещенное уравнение (21) должно иметь чисто мнимые корни z = j .

Построив границу D-разбиения для смещенного уравнения (21) в плоскости параметров К₀ и К₁ , получим всю совокупность значений К₀ и К₁, при которых m = m _зад. (рис. 8). Граница D-разбиения является линией равного m. В частном случае при m = 0 имеем границу области устойчивости.

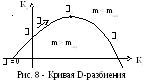
Для практических целей достаточно ограничиться положительными значениями К₀и К₁. Задаваясь различными значениями m, можно построить семейство линий равной степени колебательности (рис. 9), что позволяет производить выбор параметров регулятора.

Рассмотрим последовательность построения линий заданного значения m. Подставим в уравнение (21) z = j и e^{j k } = cos k+ j sin k, получим уравнение границы D-разбиения

(22)

К₀ К_y + К₁ К_y j  (cos  + j sin  ) + a ₀ j  (cos  + j sin ) –

- a₁ ² (cos 2 + j sin 2) – a₂ j ³(cos 3  + j sin 3) = 0

Раскрывая скобки и приравнивая к нулю вещественную и мнимую части уравнения (22), получим систему с двумя неизвестными:

(23)

-К₁ К_y sin+ К₀ К_y –а ₀sin- a₁ ²cos 2+а₂ ³sin 3= 0

К₁ К_y сos+ а ₀cos- a₁ ²sin 2- а₂ ³cos 3= 0

Необходимо помнить, что при таком выборе осей координат, как на рис. 8 и 9, первым записывается параметр К₁и уравнение для вещественной части. Решая систему (23) при различных значениях, найдем границу Д- разбиения. Решение удобно искать с помощью определителей

К

(24)

₁=; К₂=;

где -к_у sinк_у

 = = - K_y²cos;

к _у сos0

(25)

(а ₀sin+ a₁ ²cos 2- а₂ ³sin 3) к_у

₁ = =

(- а ₀  cos  + a ₁ ² sin 2  + а ₂ ³ cos 3 ) 0

= (а ₀  cos  - a ₁ ² sin 2  - а ₂ ³ cos 3 );

-sinк_у( a₀ sin + а₁²cos 2- а₂ ³sin 3)

₂= =

 cos к_у(-а₀ сos+ a₁ ²sin 2+ а₂ ³cos 3)

= - а₁ ³ (cos  cos 2  + sin  sin 2)к _у-

- а ₂ ⁴ (sin  cos 3  - cos  sin 3)к _у =

= -(a ₁ ³ cos  - a ₂ ⁴ sin 2 ) к_у .

Подставив значения,₁ и₂в (24), найдем К₁и К₀как функции:

(26)

К₁= (-а₀ + а₁+ а₂ ² )

К₀=²( a₁- 2а₂sin) / к_у .

Изменяя в пределах от 0 до, построим кривую D-разбиения. В частном случае для m = 0 (= 0) из (26) найдем уравнение границы области устойчивости

(27)

К₁= (- а₀+ а₂²) / к_у ;

К₀= а₁ ²) / к_у

или

(28)

К₁=

Для облегчения расчетов в табл. 2 приведены значения sin k, cos kдля различных значений m .

Уравнения (26), (27) можно получить по-иному, кривая D-разбиения является отображением мнимой оси z = jна плоскость коэффициентов К₁, К₀. Уравнение прямой z = jв старых координатах имеет вид

s

(29)

= - m+ j.

Подставляя в несмещенное характеристическое уравнение значение корня s = - m + jи проделав соответствующие преобразования, получим уравнения, аналогичные (26), (27), но являющиеся функциями частоты.

Второй способ требует более громоздких вычислений, и им целесообразно пользоваться при невысоком порядке характеристического уравнения.