Лекция 17.

Цель лекции: изучение ЛАЧХ и ЛФЧХ типовых звеньев САУ.

Задачи лекции:

1. Использование стандартных наклонов ЛАЧХ типовых звеньев САУ для построения ЛАЧХ САУ.

2. Определение запасов по фазе и амплитуде с помощью ЛАЧХ САУ.

Желаемый результат:

Студенты должны знать:

1. Стандартные наклоны типовых звеньев САУ;

2. Порядок построения ЛАЧХ и ЛФЧХ САУ;

3. Анализ полученных характеристик: определение низкочастотной, среднечастотной и высокочастотной зон;

4. Значения рекомендуемых значений запасов по фазе и амплитуде, определяемых по ЛАЧХ и ЛФЧХ для различного типа САУ.

Учебный материал Амлитудо-фазовые и логарифмические частотные характеристики сау

1. Безинерционное (усилительное) звено

Т.о. АФХ равна коэффициенту передачи к и обращается в точку на действительной оси на расстоянии =к от начала координат.

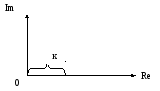
Из рисунка видно, что ни модуль, ни фаза от частоты не зависят, т.е. воздействие любой частоты, поступающее на вход этого звена усиливается в одинаковой степени без фазового сдвига.

2. Инерционное (апериодическое) звено первого порядка

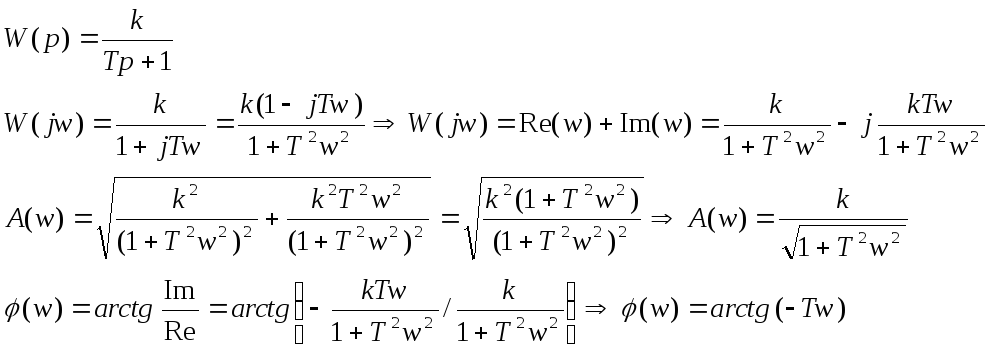
АФХ инерционного звена первого порядка – это полуокружность

Доказательство

Т.к. отношение мнимой части к действительной = -Tw, тогда

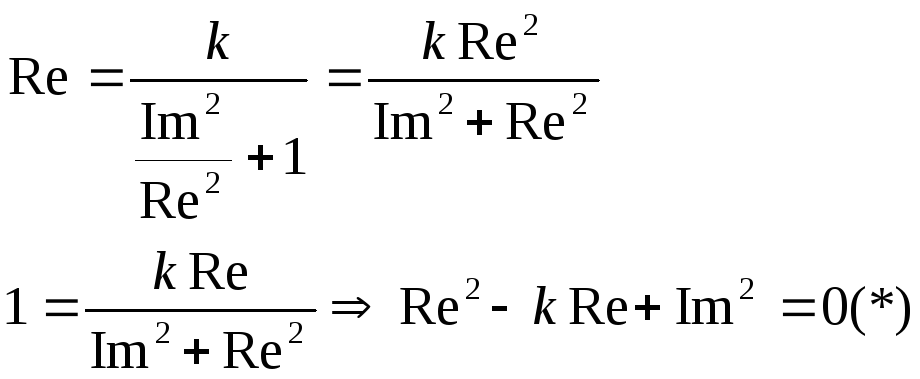
Прибавим к левой и правой части (*) к²/4

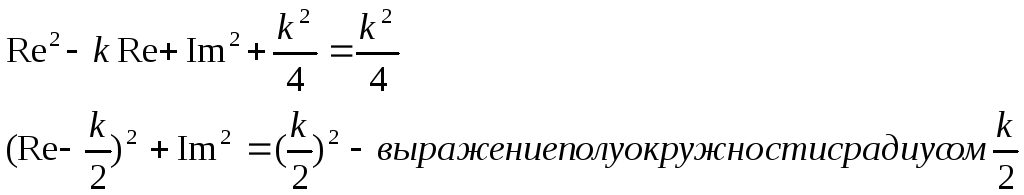
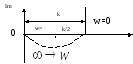
Re

Коэффициент усиления к определяется отношением амплитуд выходных и входных величин при нулевой частоте.

Логарифмическая АЧХ определяется логарифмированием модуля частотной передаточной функции.

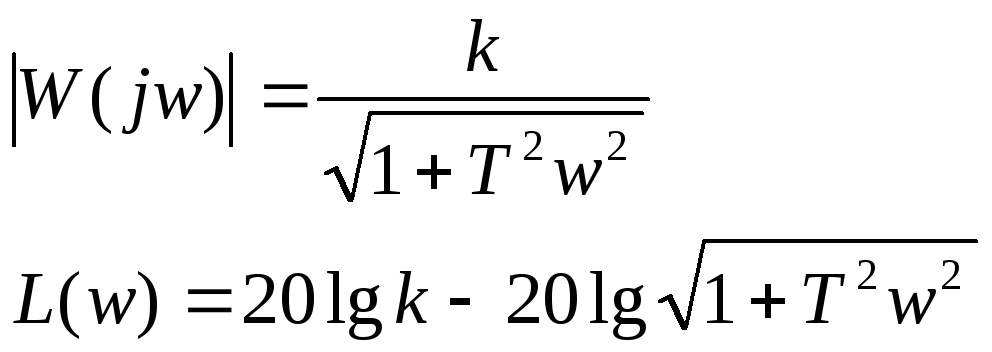
Логарифмическая АЧХ представляется ломаной линией согласно полученного выражения (хар-ка приближенная). Она называется асимптотической, т.к. она составлена из двух асимптот, к которым стремится логарифмическая АЧХ при wи w. Определим эти асимптоты:

а) при низких частотах: w<<1/T, значит: , тогдаL(w)=20lgk, т.е. логарифмическая АЧХ – это прямая, проходящая параллельно оси абсцисс на уровне 20lgk. Это первая асимптота, которая стремится L₁(w) при w

б) при высоких частота: w>>1/T, тогда , тогда это прямая, имеющая некоторый наклон.

L(w)=20lgk-20lgTw

Определим наклон второй асимптоты при изменении частоты в 10 раз, т.е. на декаду.

L(10w)-L(w)=20lgk-20lg10Tw-20lgk+20lgTw=20lgTw-20lg10Tw=20lgTw-20lg10-20lgTw=-20lg10=-20дБ/дек

Т.о. ЛАЧ апроксимируется двумя отрезками прямых: горизонтальным и отрезком с наклоном – 20дБ/дек. Точка сопряжения обеих асимптот будет удовлетворять равенству: 20lgk=20lgk-20lgTw; 20lgTw=0Tw=1w_c=1/T

w_c- частота сопряжения. Она определяет постоянную времени инерционного звена первого порядка и называется сопрягающей частотой. Погрешность от замены действительной ЛАЧ ее асимптотической не велика и при w_c=1/T составляет примерно 3 дБ.

Логарифмическая ФЧХ этого звена:

и для w_c фаза будет равна:

Л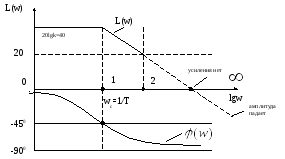ФЧХ строим по точкам относительно ординаты сопрягающей частоты для одной ветви, т.к. ЛФЧХ симметрична относительно ординаты, проходящей через точку сопрягающей частоты, то вторую ветвь проводят из условия симметрии границы изменения ЛФЧХ лежат в пределах от 0 до -/2 при изменении частоты от 0 до бесконечности.

3. Апериодическое звено второго порядка

В случае вещественных корней при t₁<t₂ апериодического звена второго порядка эквивалентно последовательному соединению двух инерционных звеньев первого порядка, поэтому его передаточная функция запишется:

Частотная передаточная функция:

к – коэффициент усиления к=к₁к₂, при Т₂<Т₁

Если Т₁=Т₂, то , его амплитудо-фазовую характеристику запишем:при Т₁=Т₂.

Выделим вещественную и мнимую части

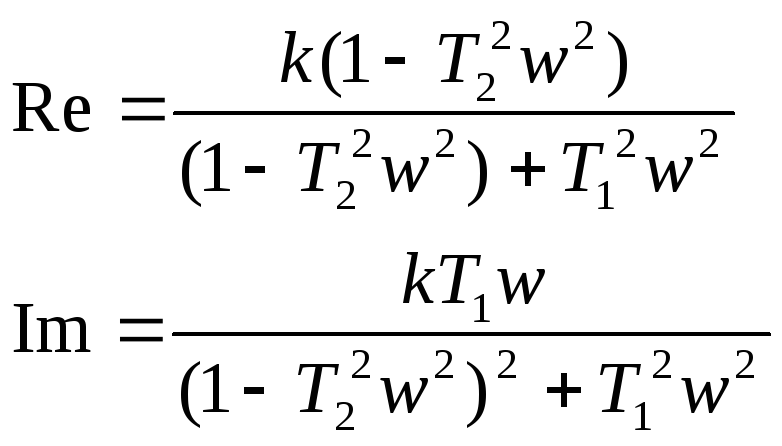
Определим АЧХ и ФЧХ

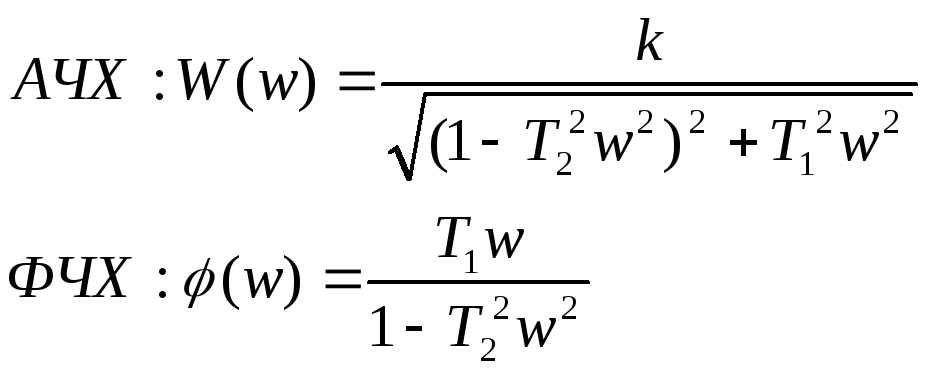
АФХ звена начинается на вещественной оси в точке с абсциссой равной к. Вид АФХ определяется отношением постоянных времени Т₁/T₂.

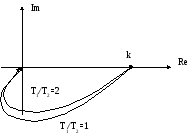
Определим ЛЧХ, аналогично тому, как это было выполнено для инерционного звена первого порядка. Можно ЛАЧХ данного звена заменить асимптотической ЛАЧХ в виде двух асимптот.

Первая асимптота w характеризует ЛАЧХ при малых частотах, тогда L(w)=20lgk-20lg можно заменить L(w)=20lgk-20lg1.

Эта асимптота представляет горизонтальную линию и не зависит от частоты.

Вторая асимптота характеризует ЛАЧХ при больших частотах, тогда

L(w)=20lgk-20lgT²w². Эта асимптота зависит от w. Чтобы установить характер этой зависимости определим приращение амплитуды в дБ при увеличении частоты в 10 раз на одну декаду.

L(10w)-L(w)=20lgk-20lgT²(10w²)-20lgk+20lgT²w²=-20lgT²w²-2*20lg10+20lgT²w²=-40lg10=-40дБ/декаду.

Сопрягающая частота w_c=1/T

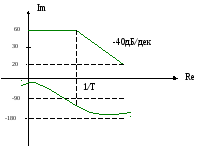
ФЧХ:

Эта функция показывает, что фаза зависит от частоты и изменяется по закону тангенсной тригонометрической функции, при w_c фаза равна -90⁰ и стремится к-180⁰ при , т.к. ФЧХ отрицательна, то выходное колебание во всем диапазоне изменения частоты отстает от входных колебаний. Для случаяT₂<T₁ построим ЛЧХ, используя их преимущества, позволяющие производить построение практически без вычислений.

Пример:

Частотная передаточная функция звена запишется в виде:

Для случая Т₂<T₁

Пусть к=100, Т₁=0,1с, Т₂=0,01с.

Имеем два последовательно соединенных инерционных звена, определим частоту сопряжения асимптот:

w₁=1/T₁=1/0,1=10c^-1

w₂=1/T₂=1/0,01=100c^-1

Построение ЛАЧХ осуществляется: при ЛАЧХ определяется:L(w)=20lgk=20lg100=40дБ

Эта хар-ка безинерционного усилителя и представляет собой прямую, проходящую на уровне 40 дБ.

В диапазоне частот w₁, w₂ общая ЛАЧХ будет определяться ЛАЧХ первого инерционного звена, т.к. при малом значении частоты w; wT₂.

Как известно ЛАЧХ инерционного звена первого порядка после частоты сопряжения w₁ представляет прямую с наклоном -20дБ/дек. Начиная с w₂ на ход характеристики начинает сказываться влияние второго инерционного звена и общая ЛАЧХ представляет прямую с наклоном -40дБ/дек. Аналогично производим построение ЛФЧХ.

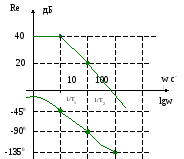
4. Дифференцирующее звено (идеальное)

W(p)=kp

W(jw)=jwk, отсюда АЧХ: W(w)=kw; ФЧХ: +arctg kw/0=

А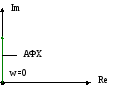ФХ диф. звена совпадает с положительной мнимой полуосью, т.к. действительная часть =0. При всех частотах выходные колебания опережают по фазе входные колебания на угол 90⁰, т.к. ФЧХ не зависит от частоты и =.

Постоим ЛАЧХ. Определяется выражением L(w)=20lgk+20lgw

Т.к. идеального диф. звена Т=0, то отсутствует частота сопряжения и прямая 20lgk вырождается в точку, характеризующую высоту проведения наклонной линии. Определим угол наклона.

L(10w)-L(w)=20lgk+20lg10+20lgw-20lgk-20lgw=20lg10=20дБ/дек

ЛАЧХ- прямая, проходящая через точку 20lgk, с наклоном 20дБ/дек

Если к=1, то прямая пройдет через начало координат

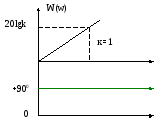
Из АЧХ следует, что больше частота входных колебаний, тем больше они усиливаются звеном. При w сигнал через звено фактически не происходит.

5. Реальное диф. звено

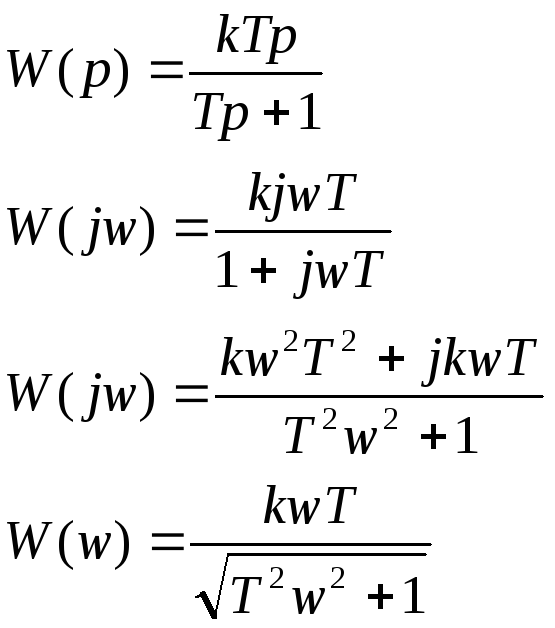
Разделяя Re и Im, определим АЧХ и ФЧХ

АФХ реального диф. звена приводится также как и для инерционного звена первого порядка к уравнению окружности. Но в этом случае при w>0 получаем полуокружность не в 4, а в 1 квадранте.

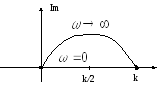
Построим ЛАЧХ по выражению:

Л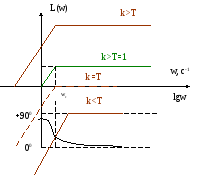АЧХ реального диф. звена представляет две асимптоты, сопрягающие наw_c=1/T. До этой частоты ЛАЧХ имеет вид прямой линии с наклоном 20дБ/дек, после w_c проходит параллельно оси абсцисс. ФЧХ определяет тангенциальной функцией частоты и при w имеет фазовый угол 90⁰, а при стремится к 0.

при k>T

k=T совпадает с lgw

6. Интегрирующее звено

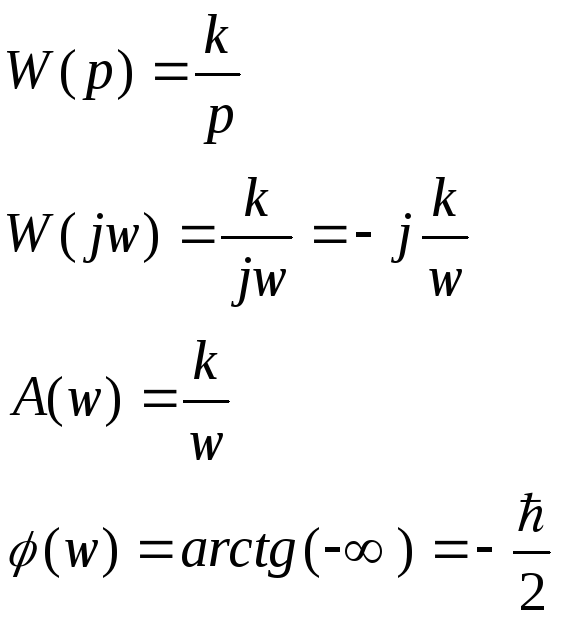
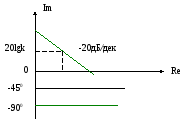
АФХ интегрирующего звена совпадает с мнимой отрицательной полуосью, т.е. с изменением w от 0 до мину бесконечности вектор АФХ движется по отрицательной мнимой полуоси от минус бесконечности до 0 при всех частотах звено создает отставание выходной величины на по сравнению с входной величиной.

Рассмотрим ЛАЧХ: L(w)=20lg k/w; L(w)=20lgk-20lgw

w=1

L(w)=20lgk

w=10

L(10)=20lgk-20lg10

L(10)-L(1)=20lgk-20lgk-20lg10=-20lg10=-20дБ/декаду

7. Колебательное звено

Если корни уравнения инерционного звена второго порядка будут комплексными, то звено колебательное, его передаточная функция:

Т₁=Т₂=Т

- параметр затухания, лежит в пределах 0<<1, т.е. Т₁/T₂<1, Т₁/T₂>0, w_c=1/T передаточная функция перепишется:

А

Im

ФХ аналогично АФХ апериодического звена второго порядка и зависит от параметра затухания.

ЛАЧХ колебательного звена строится по выражению:

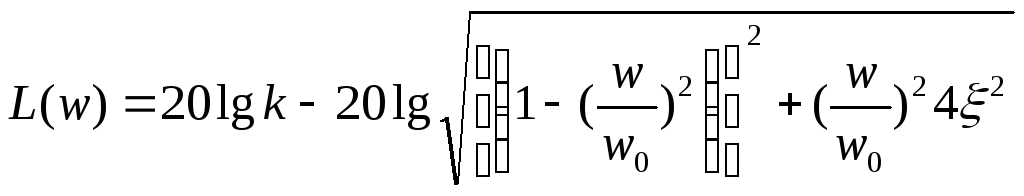
ЛАЧХ принимаем в виде двух асимптот, первая характеризует ЛАЧХ при малых частотах и равна L^’(w)20lgk-20lg1.

Вторая характеризует ЛАЧХ при больших частотах и равна

Угол наклона определим как -40 дБ/дек.

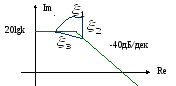
Асимптотическая ЛАЧХ получается после сопряжения обоих асимптот на сопрягающей частоте w_c=w₀=1/T. Приближенная замена ЛАЧХ допустима без введения поправки при параметре затухания , лежащем в пределах 0,4<<0,6 при других значениях рекомендуется корректировать ЛАЧХ по кривым погрешностей (справочник).

ЛФЧХ:

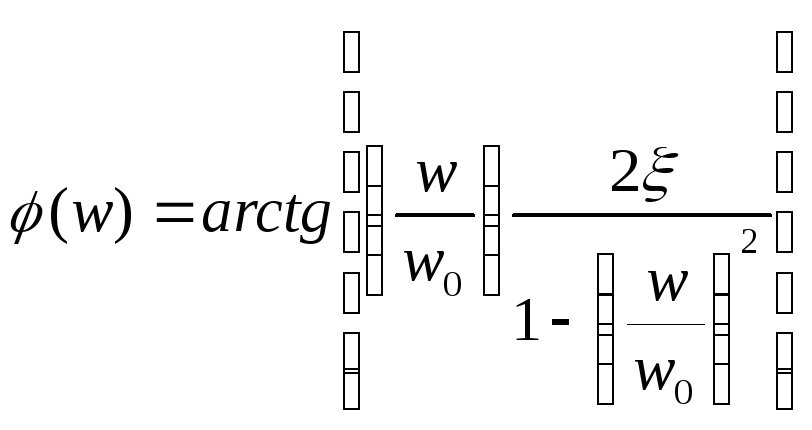
Эта функция показывает, что фаза зависит от частоты следующим образом: при сопрягающей частоте фаза =-90⁰ и ФЧХ имеет различный наклон вблизи координаты

-90⁰ при различных .

Вопросы самоконтроля:

1. Представьте порядок расчета ЛАЧХ безъинерционного звена.

2. Представьте порядок расчета ЛАЧХ апериодического звена 1-го порядка.

3. Представьте порядок расчета ЛАЧХ апериодического звена 2-го порядка.

4. Представьте порядок расчета ЛАЧХ дифференцирующего звена.

5. Представьте порядок расчета ЛАЧХ интегрирующего звена.

6. Представьте порядок расчета ЛАЧХ колебательного звена.

7. Представьте порядок расчета ЛАЧХ системы автоматического управления.

Список литературы по теме лекции:

1. Бесекерский В.А., Попов Е.П. Теория CAP, М.,2005

2. Иващенко Н.Н. Автоматическое регулирование, М.,2003