Критерий устойчивости Михайлова

Является геометрический интерпретацией принципа аргумента. Пусть дано характеристическое уравнение вида:

(9)

Полином Д(р) – характеристический полином. Для того, чтобы система была устойчивой надо, чтобы все корни хар-го ур. принадлежат левой полуплоскости (m=0). В этом случае согласно (8) должно удовлетворяться уравнение:

(10)

Из (10) следует, что все корни уравнения Д(р)=0 принадлежит левой полуплоскости. Геометрическое место точек конца вектора Д(jw) при называется годографом вектора Д(jw) или годографом Михайлова. Согласно (9) уравнение годографа Михайлова имеет вид:

(11)

где действительная и мнимая части соответственно будут равны:

U(w)=a₀-a₂w²+a₄w⁴-… (12) V(w)=a₁w-a₃w³+a₅w⁵-… (13)

Из (12) и (13) следует, что действительная часть Д(jw) является четной функцией

U(-w)=U(w) (14), а мнимая часть –нечетная функция V(-w)=-V(w) (15)

Следовательно Д(-jw)=U(w)-jV(w) (16), т.е. Д(jw) и Д(-jw) являются сопряженными комплексными величинами и следовательно запишем:

(17)

Учитывая (17) уравнение (10) можно представить:

(18)

Из (18) следует формировка критерия устойчивости Михайлова:

САР будет устойчивой, если изменении w от 0 до +вектор Д(jw) начав движение из точки, лежащей на положительной вещественной полуоси комплексной плоскости, вращаясь против часовой стрелки, и нигде не обращаясь в 0, обходит последовательно n квадратов комплексной плоскости, где n- степень характеристического уравнения.

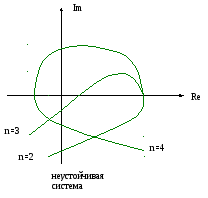
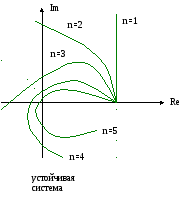
Годограф Д(jw) постоим по уравнению (12), (13), задаваясь значениям w и вычисляя U(w) и V(w). Годограф замкнутой системы можно построить, исходя из уравнения передаточной функции замкнутой системы.

Для знаменателя замкнутой системы получаем характеристический полином замкнутой системы, следовательно D(p)=A(p)+k(p), для построения годографа Д(jw) необходимо построить годографы A(jw) и k(jw) и сложить векторы A(jw) и k(jw) для каждого значения частоты. В случае, когда k(jw)=k, т.е. не зависит от w годограф Д(jw) получается простым смещением годографа A(jw) вправо вдоль вещественной оси на величину к (смещение мнимой оси к), следовательно, построив кривую Михайлова можно определить критическое значение коэффициента усиления к,т.е. то его значение, при котором система будет находиться на границе устойчивости, что соответствует прохождению кривой через начало координат.

Критерии устойчивости Найквиста

Дает возможность судить об устойчивости замкнутой системы, исследуя разомкнутой системы, что упрощает расчеты. Он позволяет судить об устойчивости замкнутой системы по экспериментально снятой характеристике разомкнутой системы, что выгодно отличает этот критерий от других.

Пусть передаточная функция разомкнутой системы:

Образуем функцию вида: (1)

Числитель представляет характеристический полином замкнутой системы. Знаменатель – характеристический полином разомкнутой системы. Степень характеристического полинома Д(p)=n, а k(p)=r, примем r<n (2)

Учитывая (2)можно утверждать, что степень полинома D(p)+k(p) также равна n. Построим 2 случая состояние разомкнутой системы: устойчивое и неустойчивое.

1) Система в разомкнутом состоянии устойчива, тогда согласно критерию Михайлова изменения аргумента характеристического уравнения разомкнутой системы определяется:

Для устойчивости системы в замкнутом состоянии должно выполняться:

(3), тогда из (1) следует, что изменение (4)

Т.о. система устойчива, если изменение аргумента вектора F(jw) при изменении 0<w<равно 0.

Годограф F(jw) для устойчивой системы, он не охватывает точку (0,0)

F(jw)- неустойчивая система, т.к. охватывает (0,0)

Передаточная функцияW_p(jw) разомкнутой системы отличается от F(jw) на (-1), то непосредственно для характеристики W_p(jw) критерий Найквиста формулиуется: Если система устойчива в разомкнутом состоянии, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы для частоты w , изменяющейся от 0 до бесконечности не охватывает точку с координатами (-1, j0).

Только в этом случае приращение аргумента F(jw)=0.

2) Система в разомкнутом состоянии неустойчива.

Характеристическое уравнение разомкнутой системы имеет m корней в правой полуплоскости. Согласно принципу аргумента:

, учитывая симметрию характеристик +w и –w можем записать:

Для устойчивости системы в замкнутом состоянии должно выполняться равенство:

При этом изменение аргумента F(jw) должно определяться:

(5)

Т.о. САУ устойчива, если изменение 0<w<годограф разомкнутой системыW_p(jw) охватывает m/2раз точку (-1, j0) в положительном направлении, где m –число корней характеристического уравнения разомкнутой системы лежащей в правой полуплоскости.

С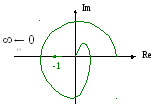истема неустойчива в разомкнутом состоянии, число корней,m=2, т.к. годограф W_p(jw) охватывает в положительном направлении точку (-1, j0), один раз, то согласно (5) замкнутая система устойчива.

Вопросы самоконтроля:

1. Дайте определение принципа аргумента.

2. Представьте порядок построения годографа Михайлова.

3. Дайте определение устойчивости по Михайлову.

4. Назовите правила построения годографа Найквиста.

5. Для каких систем определяется устойчивость по Найквисту.

6. Дайте определение устойчивости системы по Найквисту.

Список литературы по теме лекции:

1. Бесекерский В.А., Попов Е.П. Теория CAP, М.,2005

2. Иващенко Н.Н. Автоматическое регулирование, М.,2003