
- •Лекции по
- •Учебный материал. Введение, основные понятия сау. Понятие об автоматическом управлении
- •Классификация сау
- •Лекция 2. Функциональные элементы систем автоматического управления
- •Учебный материал Классификация функциональных элементов
- •Классификация сигналов, действующих в сау
- •Статические характеристики звеньев сау
- •Дифференциальная чувствительность звеньев
- •Лекция 3. Принципы управления сау
- •Учебный материал Принципы регулирования сау
- •Измерительные и исполнительные устройства
- •Лекция 4. Основные задачи автоматического управления
- •Учебный материал
- •Задачи программного управления.
- •Задачи стабилизации.
- •Лекция 5. Линеаризация уравнений и звеньев сау
- •Учебный материал Положения, лежащие в основе линеаризации.
- •Переход от дифференциального уравнения порядка nк системе изn-дифференциальных уравнений 1-го порядка
- •Геометрическая интерпретация и пример линеаризации.
- •Пример 2. Линеаризация водоема с карасями.
- •Тема 2. Линейные системы автоматического управления Лекция 6.
- •Учебный материал Вывод дифференциальных уравнений звеньев автоматики
- •Лекция 7
- •Учебный материал Передаточные функции звеньев и систем автоматического управления
- •Лекция 8.
- •Учебный материал Типовые динамические звенья автоматики
- •Лекция 9.
- •Учебный материал Передаточные функции сау
- •Лекция 10.
- •Учебный материал. Эквивалентные преобразования структурных схем
- •Основные правила эквивалентного преобразования
- •Лекция 11.
- •Учебный материал Типовые воздействия в автоматике
- •Тема 3. Частотные характеристики звеньев и систем Лекция 12.
- •Учебный материал Частотные характеристики звеньев сау
- •Лекция 13.
- •Учебный материал Порядок нахождения ачх и фчх
- •Годограф афчх инерционного звена. Звена
- •Реализация инерционного звена.
- •Логарифмические частотные характеристики инерционного звена.
- •Настоящая лачх
- •Лекция 14.
- •Операционный усилитель, охваченный комплексной оос.
- •Интегрирующее звено
- •Переходная функция интегратора
- •Весовая функция интегратора
- •Годограф афчх интегрирующего звена. Звена
- •Лачх и лфчх интегратора.
- •Точность работы такого интегратора увеличивается с ростом частоты. Именно поэтому термин "интегрирующая rCцепочка" имеет смысл.
- •Лекция 15 Реальное дифференцирующее звено. Колебательное звено.
- •Учебный материал
- •Годограф афчх реального дифференцирующего звена.
- •Колебательное звено
- •Годограф афчх инерционного звена. Звена
- •Лачх и лфчх характеристики колебательного звена.
- •Лекция 16.
- •Учебный материал Логарифмические координаты
- •Лекция 17.
- •Учебный материал Амлитудо-фазовые и логарифмические частотные характеристики сау
- •Тема 4. Структурный анализ систем автоматического управления Лекция 18.
- •Учебный материал
- •Метод последовательного логарифмирования
- •Лекция 19
- •Учебный материал
- •Блок имеет множество входов и выходов.
- •Периодическая функция с периодом т.
- •Спектр периодической функции находится в точках 2к/т.
- •Непериодическая функция.
- •Спектр непериодической функции.
- •Логарифмические частотные характеристики
- •Лекция 20 Многомерные сау со многими входами и выходами.
- •Учебный материал
- •Вобщем случае система линейных дифференциальных уравнений имеет следующий вид:
- •Тема 5. Устойчивость систем автоматического управления Лекция 21
- •Учебный материал Устойчивость систем автоматического регулирования
- •Методы определения устойчивости
- •Условие устойчивости
- •Теорема Ляпунова
- •Лекция 22
- •Учебный материал Основные критерии устойчивости:
- •Лекция 23
- •Учебный материал Частотные критерии устойчивости
- •Принцип аргумента
- •Критерий устойчивости Михайлова
- •Критерии устойчивости Найквиста
- •Лекция 24
- •Учебный материал Влияние параметров системы на ее устойчивость
- •Лекция 25
- •Учебный материал
- •Лекция 26
- •Учебный материал Понятие запаса устойчивости по амплитуде и фазе.
- •Устойчивость и запасы устойчивости на языке лачх и лфчх.
- •Влияние звена чистого запаздывания на устойчивость. Чистое запаздывание– это часть системы (цепь или блок), при прохождении которой сигнал не меняет своей формы, но задерживается на время .
- •Тема 6. Качество процессов управления Лекция 27
- •Учебный материал Качество процессов управления
- •Лекция 28
- •Учебный материал Степень устойчивости и степень колебательности систем
- •Лекция 29
- •Учебный материал Интегральные оценки качества сар
- •Порядок вычисления интегральных оценок
- •Лекция 30
- •Учебный материал Корневые критерии качества систем автоматического регулирования
- •Степень колебательности.
- •Определение параметров системы (регулятора) по заданной степени колебательности.
- •Метод смещенного уравнения.
- •Построение областей равной степени колебательности в плоскости параметров системы
- •Анализ качества регулирования.
- •Тема 7. Коррекция систем автоматического управления Лекция 31
- •Учебный материал Частотные оценки качества сар
- •Лекция 32
- •Учебный материал Синтез корректирующих устройств
- •Лекция 33
- •Учебный материал Точность сау.
- •Точность по задающему воздействию.
- •Годограф охватывает точку -1.
- •Потеря запаса устойчивости при увеличении коэффициента усиления.
- •Таким образом, увеличение коэффициента усиления разомкнутой системы уменьшает коэффициенты ошибок с0 иС1то есть, в частности, ошибку при ступенчатомUзад(t).
- •Лекция 34
- •Учебный материал Методы повышения точности сау
- •Точность по возмущающему воздействию.
- •Динамическая точность.
- •Лекция 35
- •Учебный материал Случайные процессы в сау. Линейная оптимальная фильтрация.
- •Модели случайных сигналов в сау.
- •Реализация случайного процесса
- •Типичный график корреляционной функции.
- •Регулятор
- •Фильтрация помех.
- •Лекция 36
- •Учебный материал Нелинейные системы автоматического управления
- •Лекция 37
- •Учебный материал Основные виды нелинейностей в сау
- •Лекция 38
- •Учебный материал Релейные элементы-
- •Лекция 39
- •Учебный материал Методы исследования нелинейных систем
- •Лекция 40
- •Учебный материал Характеристики нелинейных систем
- •Метод фазовой плоскости (фазовой траектории)
- •Лекция 41
- •Учебный материал Метод изоклин
- •Метод припасовывания (сшивания).
- •Лекция 42
- •Учебный материал Особые траектории
- •На рис.2 представлена фазовая плоскость хар-ся устойчивым фокусом и неустойчивым предельным циклом.
- •Лекция 43
- •Учебный материал
- •В результате получим следующие значения амплитуды, частоты и периода:
- •Лекция 44
- •Учебный материал Получение кривой переходного процесса по фазовой траектории системы (графический метод)
- •1. Аппроксимируем фаз.Траекторию отрезками прямых 21, 32, 43…
- •Метод гармонического баланса
- •Лекция 45
- •Учебный материал Метод гармонической линеаризации
- •Основное уравнение гармонического баланса
- •Лекция 46
- •Учебный материал Способ Гольдфарба
- •Способ Коченбургера
- •Лекция 47
- •Учебный материал Способ Попова
- •Влияние параметров системы на автоколебания
- •Условие применимости метода гармонического баланса
- •Метод малого параметра
- •Назовите условие применимости метода гармонического баланса
- •Выделение отдельных составляющих движения
- •Лекция 49
- •Учебный материал Основные теоремы метода разделения движений
- •Условия применимости метода
- •Лекция 50
- •Учебный материал Импульсные системы
- •Варианты выходных последовательностей импульсных звеньев
- •Дискретные системы автоматического управления. Типы дискретизации. Структурные схемы импульсных систем
- •Лекция 51
- •Учебный материал Понятие решетчатой и модулированной функций. Дискретное преобразование Лапласа
- •Дифференцирование и интегрирование решетчатых функций
- •Лекция 52
- •Учебный материал Исследование устойчивости системы по разностному уравнению
- •Критерий устойчивости импульсных систем
- •Лекция 53
- •Учебный материал Свойства дискретного преобразования Лапласа
- •Лекция 54
- •Учебный материал Случайные процессы в системах автоматического регулирования.
- •Лекция 55
- •Учебный материал Случайные процессы
- •Лекция 56
- •Учебный материал Стационарные случайные процессы
- •Лекция 57
- •Учебный материал Корреляционная функция
- •Лекция 58
- •Учебный материал Спектральная плотность стационарных процессов
- •Спектральная плотность вычисляется по известной корреляционной функции при помощи формул.
- •Лекция 59
- •Учебный материал Расчеты по минимуму среднеквадратичной ошибки
- •Глоссарий
- •Основная и дополнительная литература
Фильтрация помех.
Теперь перейдём собственно к постановке и решению задачи фильтрации, понимаемой нами, как задача борьбы с помехами в САУ. Будем при этом решать задачу как оптимальную, то есть искать условия наибольшего подавления помех. Помехи будем считать случайными процессами с известными корреляционными функциями или (что эквивалентно) с известными спектральными характеристиками.
Фильтр Винера (Норберт Винер).
З адача
- построить устройство-фильтр в виде
передаточной функции, максимально
возможно подавляющееаддитивную
случайную
помеху. При этом полезный сигнал также
считается случайным процессом. Возможность
эффективной фильтрации зависит от того,
как перекрываются спектры полезного
сигнала и помехи, но не только от этого.
Важна ещё и степень статистической
связи между ними, которая описывается
взаимной спектральной плотностью или
взаимной корреляционной функцией.
адача
- построить устройство-фильтр в виде
передаточной функции, максимально
возможно подавляющееаддитивную
случайную
помеху. При этом полезный сигнал также
считается случайным процессом. Возможность
эффективной фильтрации зависит от того,
как перекрываются спектры полезного
сигнала и помехи, но не только от этого.
Важна ещё и степень статистической
связи между ними, которая описывается
взаимной спектральной плотностью или
взаимной корреляционной функцией.
Предполагаются известными:
спектральная плотность полезного сигнала Sx(), а также их взаимная спектральная плотность Sxv(), либо, что эквивалентно:
с![]() оответствующие
корреляционные функцииKx(),
Kxv().
оответствующие
корреляционные функцииKx(),
Kxv().

![]() V(p)
V(p)
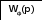 X(p) X+V
(p)
X(p) X+V
(p)




![]() e(t)=x(t)-
(t); (79)
e(t)=x(t)-
(t); (79)
Случайный процесс e(t)=x(t)- (t) называется ошибкой фильтрации. Его "малость" могла бы означать хорошее качество фильтрации, однако, для случайной величины понятие "малость" не имеет обычного смысла. Вместо этого используют малость дисперсии De, как меры мощности сигнала e(t).
Оптимальная передаточная функция фильтра ищется из условия:
Demin
Отметим, что важным предположением является стационарность случайных сигналов и отсутствие дополнительной информации о сигналах, при наличии которой фильтрацию можно было бы улучшить.
Имеются формулы, позволяющие получить передаточную функцию оптимального фильтра Винера, наилучшим образом решающую задачу:
![]()
здесь: К+(p) - устойчивые элементарные дроби в разложении К(p).
Рассмотренный фильтр Винера описывает процедуру стационарной фильтрации при стационарных случайных процессах. При этом не учитываются, например, переходные процессы при заданном начальном состоянии системы. Фильтр Винера может быть обобщён на более сложные случаи (многомерных сигналов, нестационарных процессов и т.п.), но наиболее полным образом теория и задача линейной фильтрации реализуется в так называемом фильтре Калмана, то есть в многомерном, нестационарнм линейном оптимальном фильтре в пространстве состояний.
Конечно, фильтр Винера оказывается частным случаем фильтра Калмана, именно - установившимся режимом фильтра Калмана при стационарных помехах, представленным в виде передаточной функции.
Вопросы самоконтроля:
Дайте определение слученных процессов в САУ?
Дайте определение случайного стационарного процесса?
Какими математическими понятиями описываются случайные процессы в САУ?
Как производится фильтрация помех?
Лекция 36
Цель лекции: изучить основные понятия нелинейных систем автоматического управления.
Задачи лекции:
Определение нелинейных САУ.
Классификация нелинейных характеристик звеньев и систем.
Желаемый результат:
Студенты должны знать:
Основные понятия нелинейных САУ;
Виды нелинейностей звеньев;
Методы определения нелинейности систем.
