Тема 2. Линейные системы автоматического управления Лекция 6.

Цель лекции: рассмотреть соотношение сил действующих в звеньях автоматики на примере механического звена; подучить дифференциальное уравнение звена автоматики.

Задачи лекции:

1. Вывод дифференциальных уравнений звеньев автоматики.

2. Постоянные времени в дифференциальных уравнениях звеньев.

3. Устойчивое состояние звена.

Желаемый результат:

Студенты должны знать:

• Порядок расчета дифференциальных уравнений звеньев САУ;

• Определение характеристического уравнения звеньев САУ;

• Порядок вычисления корней характеристических уравнений звеньев САУ;

• Все случаи сочетания корней характеристического уравнения звеньев САУ.

Учебный материал Вывод дифференциальных уравнений звеньев автоматики

Рассмотрим силовые соотношения для механического звена с выходной координатой в виде перемещения. Пусть в пространстве звено укреплено специальным образом на пружинных растяжках, назовем его муфтой.

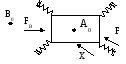
т.А₀ – центр масс

Положение точки А₀ определяется факторами:

1. масса пружин

2. жесткость пружины

3. количество и пространственное положение пружин

любая конструкция пружин и их расположения в пространстве обеспечивают как минимум одну устойчивую точку, при этом муфта находится в покое. Если в некоторый момент воздействовать на муфту силой F в направлении X, то выходная координата уже не равна равновесной (yy₀). Центр масс перемещается в т. В₀ и главный вектор всех сил, действующих на муфту не равен 0. эта равнодействующая называется восстанавливающей силой F_в звена. Восстанавливающая сила стремится возвратить центр масс из т. В₀ в т. А₀. численно восстанавливающая сила равна силе, которая надо приложить к муфте, чтобы удержать ее в т. В₀ (F_в=F). В общем случае восстанавливающая сила функционально связана с обеими координатами x и y. В координатной плоскости xy восстанавливающую силу можно изобразить вектором, направленным параллельно оси y в сторону изменения величины выходной координаты.

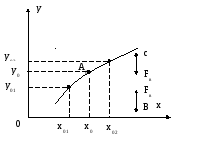
Для точки А₀, лежащей на равновесной характеристике, восстанавливающая сила равна 0. для точки В, у которой координата y<y₀ восстанавливающая сила > 0 и направлена вверх, в сторону увеличения y. Для точки c, у которой координата y>y₀. восстанавливающая сила <0, направлена вниз в сторону уменьшения y. Если изменить начальные условия, то начальное (равновесное положение муфты) будет другим. Бесконечно изменяя факторы (*) получим геометрическое место точек равновесного положения или кривую устойчивости. Пусть возмущающая сила снята, тогда муфта устремится в исходное положение каким-либо (каким неизвестно) образом.

Значит перед нами стоит задача:

Вывести дифференциальное уравнение движения муфты; решить его; получить условия, при которых муфта возвращается в исходное состояние необходимым нам образом.

Пусть имело место равновесное состояние при координатах (x₀, y₀). Приведенную к муфте массу движущихся частей обозначим через m. Тогда уравнение движения муфты опишется вторым законом Ньютона.

(1)

F_c - сила сопротивления, включающая силу трения.

Из всех сил F_c будем учитывать только силу вязкого трения, пропорциональной скорости перемещения.

имеем (2) -

- исходное уравнение движения муфты.

Введем отклонение от устойчивого равновесия:

y, x – текущие значения входных и выходных координат

- отклонения текущих значений входных и выходных координат

x₀, y₀ – значения координат равновесного состояния

Исходная величина восстанавливающей силы, при равновесном состоянии звена, т.е. в момент x=x₀, y=y₀, тогда F_в=А_в0 при (x₀, y₀) и равно 0, т.е. F_в=F_в0(x₀, y₀)=0

Используя разложение в ряд Тейлора функции двух переменных с учетом двух первых членов разложения

(3)

Индекс О, причастный к производной, указывает, что учитываются их частные значения при равновесном состоянии, т.е. при x=x₀, y=y₀.

Из (2) с учетом (3) следует:

(4)

Введем безразмерные координаты

В уравнении (4)

имеем

(5)

Приведем коэффициент при безразмерной входной координате к 1(6)

Коэффициент при второй производной выходной координаты имеет размерность время в квадрате, а при первой производной имеет размерность время, а коэффициент при безразмерной выходной координате безмерной. Значит обозначим коэффициент при второй производной:

, то имеем

(7)

Получаем линеаризированное уравнение звена второго порядка.

Т₁-поятоянная времени, характеризует инерционность звена, численно равна половине квадрата времени необходимого для перемещения муфты от исходного предельного (y=0) до равновесного (y=y₀) положения при максимальной восстанавливающей силе (x=x₀) и отсутствии сопротивления.

Т₂- постоянная времени, характеризует величину сопротивления перемещения звена, численно равна времени равномерного перемещения муфты от исходного, т.е. предельного положения до равновесного с такой скоростью, при которой сила сопротивления достигнет максимального значения восстанавливающей силы.

, Т₂ всегда > 0

Т₂ может равняться 0 при в=0 (при отсутствии вязкого трения).

Рассмотрим установившееся положение звена

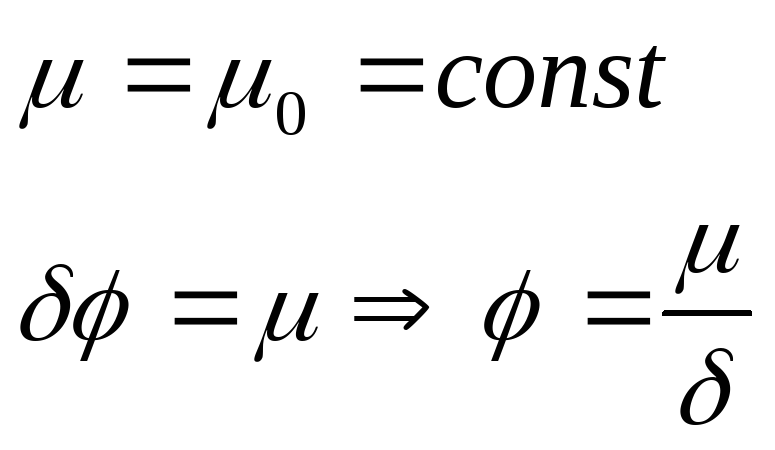
-коэффициент передачи, который характеризует, на сколько или во сколько раз изменяется выходной сигнал муфты при воздействии данного входного.

(9)

(коэффициент статизма)

тогда (7) перепишется (8)

Решение дифференциального уравнения (8)

В виде суммы общих и частных решений: общая (с нулевой частью); частное (все производные равные 0) (9)

(10) - характеризует свободное движение звена, т.е. его поведение при отсутствии внешнего воздействия.

(11),

где С₁, С₂ – постоянные интегрирования

-корни характеристического уравнения

Характеристическое уравнение имеет вид:

-

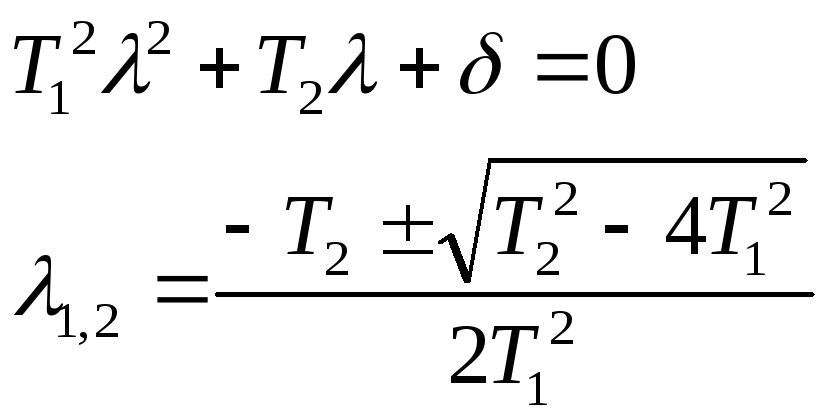
размерность: время в (-1) степени

- безразмерный коэффициент в (11)

Рассмотрим все случаи сочетания корней характеристического уравнения, считая, что на вход звена подано единичное скачкообразное, входное воздействие , тогда частное решение будет:- значение выходной координаты в установившемся режиме.

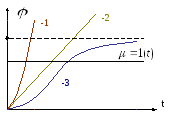
1- корни действительные и > 0

Переходный процесс будет идти (1) (неустойчивое движение муфты)

2- корни действительные

3- корни действительные . Устойчивое движение муфты (муфта переходит из одного устойчивого положения в другое устойчивое положение)

4- корни действительные (устойчивое движение муфты с перерегулированием)

5- корни комплексные взаимосопряженные

Муфта содержит устойчивые колебательные движения с затуханием

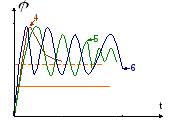
6- корни взаимосопряженные, мнимые. Движение муфты осуществляется на границе устойчивости, и она совершает период, незатухающие колебания.

Вопросы самоконтроля:

1. Дать определение силам действующим на механическое звено автоматики.

2. Дать определение отклонению от устойчивого положения

3. Дать определение характеристического уравнения звена автоматической системы.

4. Дать определение установившемуся движению звена автоматической системы.

5. Дать определение колебательного процесса звена автоматической системы.

Список литературы по теме лекции:

1. Бесекерский В.А., Попов Е.П. Теория CAP, М.,2005

2. Иващенко Н.Н. Автоматическое регулирование, М.,2003