Лекция 5. Линеаризация уравнений и звеньев сау

Цель лекции: изучение математических принципов проведения линеаризации уравнений САУ.

Задачи лекции:

1. Изучение положений, лежащих в основе линеаризации.

2. Изучить переходный процесс системы.

3. Изучить порядок линеаризации статических характеристик систем управления.

Желаемый результат:

Студенты должны знать:

• Порядок проведения линеаризации статических характеристик систем управления;

• Порядок построения переходного процесса системы.

Учебный материал Положения, лежащие в основе линеаризации.

Линеаризация заключается в переходе к линейному дифференциальному уравнению, переменные которого являются отклонениями от некоторого номинального режима, удовлетворяющего уравнению (**).

Вычислим дифференциал F в (*), введя предварительно следующие обозначения:

Z = (y', y'', ... y⁽ⁿ⁾);

U = (u', u'', ... u^(m));

F(Z,U)=0; (**)

Пусть Z_н и U_н - номинальная траектория, удовлетворяющая (**)

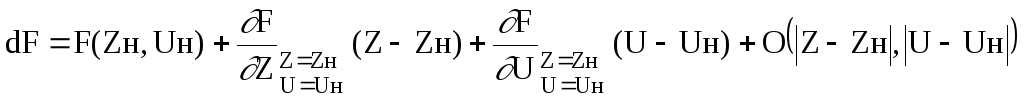
F(Zн,U_н)=0 т.к. траектория номинальная. Отбрасываем малые члены:

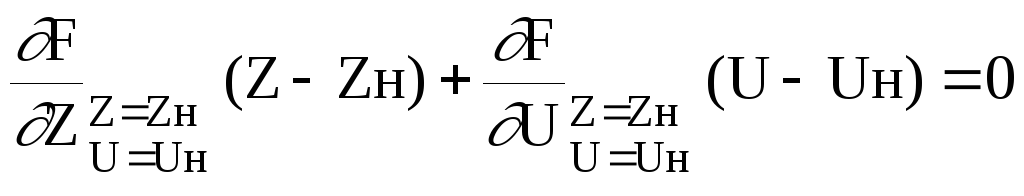
- линеаризованное уравнение.

При этом - коэффициенты ряда Тейлора.

Введем новые переменные - отклонения от номинальных: y = y-y_н

и u = u-u_н

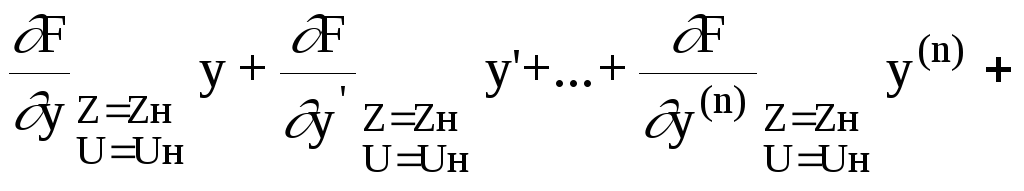
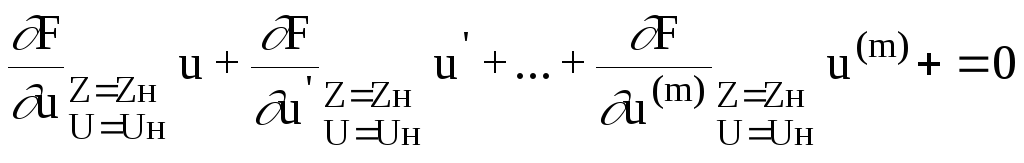
Так как все частные производные представляют из себя либо постоянные матрицы, либо, в крайнем случае, матрицы зависящие только от времени, то полученное уравнение (3) есть либо система линейных дифференциальных уравнений с постоянными коэффициентами относительно отклонений y и u, либо система с переменными коэффициентами. Постоянcтво или переменность зависит от номинальной траектории. В частности, в системах стабилизации, где номинальные траектории - константы, получаются постоянные матрицы.

Таким образом, перейдя к уравнениям в отклонениях, мы получаем систему линейных дифференциальных уравнений, которую рассматриваем относительно выходной величины. Порядок этой системы линейных дифференциальных уравнений равен n по порядку производной при y.

Дифференцирование же входного сигнала u рассматривается не как дифференциальное уравнение относительно u , а как операция с известным входным сигналом.

Соберем все коэффициенты дифференциальных уравнений в матрицы и получим окончательно следующую матричную систему:

A₀(t)y⁽ⁿ⁾ + A₁(t)y^(n-1)+…+A_n(t)y=B₀(t)u^(m)+…+B_m(t)u

Если удаётся удачно выбрать номинальную траекторию (это зависит не только от мастерства исследователя, но и от самой задачи), матрицы А_i и B_i становятся постоянными. И для такой системы линейных дифференциальных уравнений с постоянными коэффициентами можно получить до конца точное решение и полностью его исследовать. В случае постоянных коэффициентов система называется стационарной.

Чаще всего оказывается, что входные и выходные величины объекта - скалярные функции. То есть имеется лишь по одному входу и выходу, матрицы превращаются в числа, а (4) принимает вид (5):

a₀y⁽ⁿ⁾+…+a_ny=b₀u^(m)+…+b_mu

Получили стационарный объект с одним входом и выходом (скалярный).

Именно такие скалярные стационарные объекты являются главным объектом исследования в классической ТАУ.