Порядок вычисления интегральных оценок

Если известна передаточная функция системы и на вход системы поступило единичное ступенчатое воздействие, то значение линейной интегральной оценки находится:

1. Преобразуем по Лапласу выражение для динамической ошибки переходного процесса: y(t)=x₀-x(t) (5)

x₀ – установившееся значение выходной величины после окончания переходного процесса.

x(t)- текущее переменное значение выходной величины в течении переходного процесса.

(5а)

(5б)

5а и 5б5:(6)

Полагаем, что оператор р0 в выражении преобразования Лапласа:

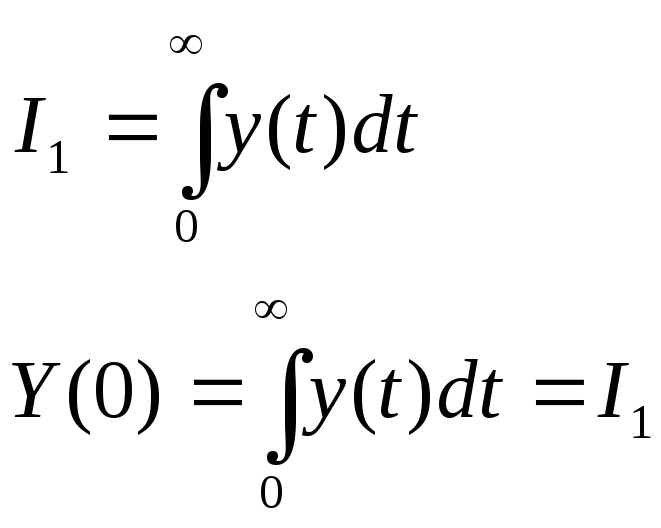
Т.о. линейная интегральная оценка качества I₁ при поступлении на вход САР единичного ступенчатого воздействия определяется через значения передаточной функции замкнутой системы для установившегося и неустановившегося ее состояний: (7)

Пример: САР, являющаяся в динамическом отношении инерционным звеном первого порядка с передаточной функцией: W(p)=k/Tp+1

Решение:

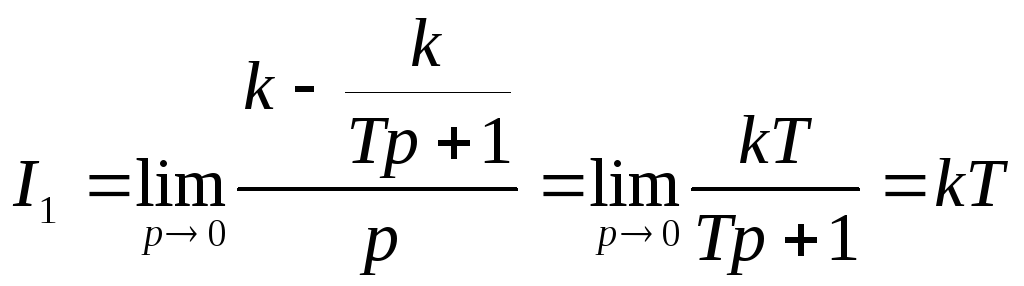
Варьируя к_{усиления} и Т времени можно получить различные I₁.

Вопросы самоконтроля:

1. Назовите порядок построения кривых для определения интегральных оценок качества САУ.

2. Дайте определение квадратичным интегральным оценкам качества САУ.

Список литературы по теме лекции:

1. Бесекерский В.А., Попов Е.П. Теория CAP, М.,2005

2. Иващенко Н.Н. Автоматическое регулирование, М.,2003

Лекция 30

Цель лекции: изучение корневых критериев качества САР.

Задачи лекции:

1. Понятие корневых критериев качества САУ.

2. Определение параметров системы (регулятора) по заданной степени колебательности.

3. Метод смещенного уравнения.

4. Построение областей равной степени колебательности

в плоскости параметров системы

5. Анализ качества регулирования.

Желаемый результат:

Студенты должны знать:

1. Порядок определения параметров системы (регулятора) по заданной степени колебательности.

2. Метод смещенного уравнения.

3. Порядок построения областей равной степени колебательности

в плоскости параметров системы

4. Порядок анализа качества регулирования.

Учебный материал Корневые критерии качества систем автоматического регулирования

Корневые критерии составляют отдельную группу косвенных критериев качества. Известно, что переходный процесс в линейной системе описывается выражением

у

(1)

(t) =у_i (t) + у_уст.(t) =C_i + у_уст.(t),

где у_i (t) – переходная составляющая;

У_уст - установившаяся (вынужденная) составляющая переходного

процесса;

s_i - корни характеристического уравнения замкнутой системы;

С_i – постоянные интегрирования.

Качество регулирования существенно зависит от корней характеристического уравнения. Корневые критерии позволяют оценивать качество регулирования по распределению корней характеристического уравнения. При этом совершенно не обязательно знать значения корней, а достаточно знать область, где они расположены. Наиболее распространенным корневым критерием является степень колебательности m, которая достаточно точно характеризует степень затухания переходного процесса .

Степень колебательности.

Рассмотрим переходную составляющую, соответствующую комплексно- сопряженным корням

s

(2)

_{i, i+1} =  α _i  j_i

у_i (t)= C_i ·sin (_it +_i)

Одним из основных показателей качества переходного процесса является степень затухания , определяемая следующим образом (рис.2).

(3)

Степень затухания  характеризует интенсивность затухания переходного процесса и для устойчивой системы изменяется в пределах

0

(4)

‹ ‹ 1.

Если процесс незатухающий (система на границе устойчивости), то

А₃ = А₁ и  = 0. Если же А₃ = 0, то  = 1. Чем выше , тем интенсивнее затухает переходный процесс. Считается, что значение  должно лежать в пределах

0

(5)

,75 ≤ ≤ 0,9.

При этом система имеет удовлетворительные показатели качества. Подставляя в формулу (3) значения А₁ и А₃, определяем из (2) и рис.2

; ;

получим



(6)

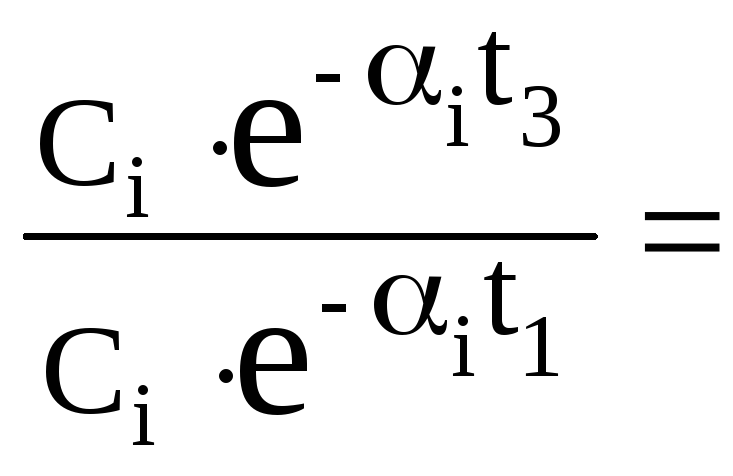_i (t) = 1 ―1

Учитывая, что t₃ = t₁ +, получим окончательно



(7)

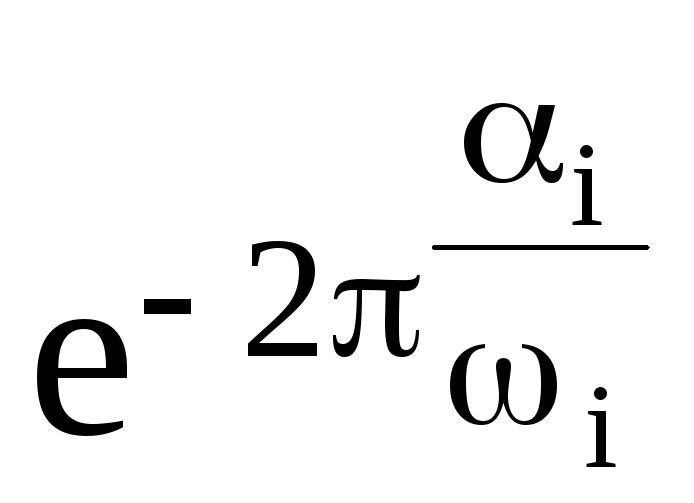_i (t) = 1 ― =1 –,

где  отношение модулей действительной и мнимой частей корня. Как следует из формулы (7), степень затухания переходной составляющей зависит лишь от отношения , т.е_i = _i (m _i). Причем с увеличением m степень затухания  также растет.

Если для всех корней характеристического уравнения выполняется условие

(8)

= m_i  m_зад (i = 1, 2, … n),

где m _зад. – некоторая заданная величина, то все составляющие переходного процесса будут иметь степень затухания _i не ниже заданной  _зад.



(9)

_i   _зад. (m _зад.).

Можно ожидать, что и степень затухания суммарного переходного процесса будет близка к заданной. Следует иметь в виду, что при наложении переходных составляющих, удовлетворяющих условию _i   _зад., результирующая составляющая может иметь    _зад . На рис. 3 приведено распределение корней характеристического уравнения некоторой системы 5-го порядка.

Геометрически величина m_i = _i / _i характеризует тангенс угла наклона луча, проведенного из начала координат плоскости Р через точку Р_i к мнимой оси

m

(10)

_i = tg _i ,

_i = arctg m _{i .}

Чем больше угол наклона _i , тем выше m _{i .} Для действительных корней _i =  / 2 и m _i =  (_i =1). Минимальное значение отношения

(11)

= =m, i = 1, 2, … , n.

называется степенью колебательности системы и обозначается буквой m .

Так, на рис. 3 степень колебательности системы равна

m

(12)

= m₁ = α₁ / ω_1.

Степень колебательности m может служить критерием качества системы и в общем случае характеризует ее степень затухания. Для того, чтобы система имела степень колебательности не ниже заданной (m  m _зад. или _i   _зад.), необходимо, чтобы все корни характеристического уравнения лежали внутри области, ограниченной лучами (рис. 4), проведенными из начала координат под углом  = arctg m к мнимой оси.

Таким образом, требование m = m_зад. накладывает ограничения на область расположения корней характеристического уравнения. Точные значения корней при этом могут быть неизвестны.

Для всех корней, лежащих на границе области (рис.4),

α_i / ω_i = m_зад. или α_i = ω_i  m_зад. .

Отсюда уравнение границы области m  m_зад. в плоскости S имеет вид

s

(13)

= - m_зад. + j.