Лекция 32

Цель лекции: изучение коррекции характеристик САУ, построение ЛАЧХ корректирующих устройств САУ, последовательные корректирующие устройства, параллельные корректирующие устройства, последовательно-параллельные корректирующие устройства.

Задачи лекции:

1. Понятие необходимости коррекции характеристик САУ.

2. Графическое построение ЛАЧХ корректирующих устройств САУ различного типа.

3. Реализация корректирующих устройств САУ.

Желаемый результат:

Студенты должны знать:

1. Порядок построения ЛАЧХ последовательных, параллельные, последовательно-параллельных корректирующих устройтсв САУ;

2. Порядок расчета передаточной функции корректирующего устройства;

3. Виды реализации корректирующих устройств САУ.

Учебный материал Синтез корректирующих устройств

Работоспособная система является устойчивой. Устойчивость системы проверяется по одному из критериев на основе коэффициентов характеристических уравнений. Если система не устойчива, то, изменяя коэффициенты уравнения и соответственно конструктивные параметры системы, можно добиться устойчивости. Однако некоторые узлы системы не имеют регулировок и не изменяются. Тогда добиться устойчивости такой системы можно только включением в нее дополнительных устройств, называемых корректирующими.

В ряде случаев СУ устойчива, но показатели качества не удовлетворяют. В таких случаях в СУ включают корректирующие устройства, улучшающие качества управления. Такие устройства включаются в систему по-разному и по способу включения делятся на последовательные, параллельные и встречно-параллельные устройства.

Последовательные корректирующие устройства.

Последовательные корректирующие устройства включают в прямую цепь системы по одному из следующих вариантов.

а)

б)

Для обоих вариантов передаточная функция разомкнутой цепи одинакова:

, однако вариант (а) предпочтительней. Причина в том, что на выходе элемента сравнения формируется слабый сигнал, для варианта (б) дополнительно ослабляет его. Уровень сигнала может оказаться ниже уровня шумов. В результате вариант (б) начинает работать неустойчиво.обычно в системе является усилителем, поэтому для варианта (а) уровень сигнала поднимается выше уровня шумов и система функционирует стабильно.

Встречно-параллельное корректирующее устройство.

Пусть в системе с элементами звенонарушает качество. Параллельно этому звену включаем корректирующее звенов соответствии с рис.:

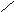
При таком включении образует отрицательную обратную связь, поэтому эквивалентная передаточная функция для скорректированного звена:

(1)

Для большинства систем , поэтому

(2)

Получили, что выражение (2) не содержит передаточной функции , поэтому отрицательное включение этого звена устранено или ослаблено. Качестве корректирующих элементов применяют жесткую и гибкую обратные связи.

Пусть прямое звено имеет передаточную функцию , а коррекция для жесткой обратной связи, для гибкойили.

Жесткие обратные связи действуют в системе непрерывно, а гибкие проявляют себя только на переходных процессах. Скорректированное звено имеет передаточную функцию:

(3)

Рассмотрим результат коррекции для частных случаев прямых звеньев и обратных коррективных связей.

1) Пусть прямое звено апериодическое , а обратная связь жесткая, т.е..

Тогда (4)

Получили, что скорректированное звено осталось апериодическим, но параметры звена иизменились.

2) Пусть исходное звено апериодическое, а обратная связь гибкая, т.е. . При этом

(5)

Получили, что гибкая обратная связь не изменяет характер звена, но изменяет постоянную времени.

3) Пусть прямое звено интегрирующее, т.е. . Обратная связь жесткая, т.е., тогда(6)

Получили, что исходное интегральное звено скорректировано до апериодического, т.е. жесткая обратная связь изменило само звено.

4) Пусть исходное звено интегрирующее, а обратная связь гибкая, т.е. , тогда

(7)

Таким образом, гибкая обратная связь не изменила характер интегрирующего звена, а изменила коэффициент передачи.

5) Пусть исходное звено колебательное, а обратная связь жесткая, т.е. ,. При этом

(8)

Получили, что жесткая обратная связь не изменила характер звена, но изменила все его параметры .

6) Пусть исходное звено колебательное, а обратная связь гибкая, т.е. , тогда

(9)

Формально выражение (9) соответствует колебательному звену. Для однозначности утверждения необходимо, чтобы

, т.е. (10).

Условие (10) определяет при каких значениях коэффициента корректирующего звена, исходное звено сохраняет свою структуру. Обратная связь, при которой характер звена не изменяется, называется слабой. Пусть, тогдаудовлетворяет условию.

Обратная связь, при таких условиях называется сильной. означает, что звено преобразовано в апериодическое 2-го порядка. Таким образом, одна и та же гибкая обратная связь может влиять на звено по-разному.

7) Пусть исходное звено пропорциональное, т.е. , а в качестве обратной связи используем апериодическое звено, т.е.. В этом случае

(11)

Скобка числителя выражения (11) соответствует форсирующему звену. В исходных звеньях его не было совсем. Таким образом, коррекция привела к появлению нового звена. Структура исходного звена изменилось.

Параллельное корректирующее устройство.

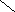
В результате корректирующего звена получим эквивалентную передаточную функцию:(1)

Для определенности предположим, что основное звено пропорциональное , а корректирующее звено апериодическое, т.е., тогда

В результате получили: в звене появилась форсирующая составляющая, в этом смысле результат параллельной коррекции эквивалентен результату от втречно-параллельной коррекции.

Формула перехода от корректирующих устройств одного типа к корректирующим устройствам другого.

Пусть в одной и той же системе с элементами поочередно применены последовательные, параллельные и встречно-параллельные коррекции. Для каждого случая вычислим передаточную функцию разомкнутой цепи.

Для 1-го случая: .

Для 2-го случая: .

Для 3-го случая: .

Потребуем, чтобы результат коррекции во всех трех случаях был одинаковым, т.е. или;

(*)

Выражение (*) позволяет по заданному встречно-параллельному или параллельному

Корректирующему устройству перейти к эквивалентному последовательному и наоборот. При проектировании корректирующих устройств вычислить все три типа и сравнить их возможности между собой, для реализации выбрать тот, который является наиболее простым.

В ряде случаев корректирующие устройства имеют сложную передаточную функцию и их реализация затруднительна. Тогда корректирующие устройства разбивают на несколько. При чем одну часть корректирующего устройства можно выбрать параллельной, а другую – последовательной.

Вопросы самоконтроля:

1. Как получить передаточную функцию последовательного корректирующего устройства?

2. Как получить передаточную функцию параллельного корректирующего устройства?

3. Как получить передаточную функцию последовательно- параллельного корректирующего устройства?

4. Перечислите правила записи передаточной функции корректирующего устройства САУ?

5. Как реализуется корректирующее устройство САУ?

Список литературы по теме лекции:

1. Бесекерский В.А., Попов Е.П. Теория CAP, М.,2005

2. Иващенко Н.Н. Автоматическое регулирование, М.,2003