Тема 5. Устойчивость систем автоматического управления Лекция 21

Цель лекции: изучить понятие устойчивости САУ.

Задачи лекции:

1. Устойчивость системы в малом и большом.

2. Методы определения устойчивости САУ.

3. Теорема Ляпунова.

Желаемый результат:

Студенты должны знать:

1. Определение устойчивости САУ в малом;

2. Определение устойчивости САУ в целом;

3. Определение устойчивости САУ по Ляпунову.

Учебный материал Устойчивость систем автоматического регулирования

Наиболее важными динамическими свойствами системы являются: устойчивость, время регулирования, время перерегулирования, число колебаний регулируемой величины. Основная характеристика: устойчивость, т.к. три последних требования могут измениться в зависимости от назначения и условий работы установки, а требования устойчивости должно удовлетворять САУ. В зависимости от характера переходного процесса линеаризованной системы различают три основных случая поведения системы после возмущающего воздействия: 1) система не может восстановить равновесное состояние, значения управляемой переменной (выходной величины) все больше откланяется от заданного, такой процесс называется расходящимся, а система неустойчивой; 2) Система возвращается в равновесное состояние значение управляемой переменной отличается от заданного на величину статической ошибки, такой процесс называется сходящимся, а система устойчивой; 3) Система характеризуется установившимся периодическим движением, такой процесс называется колебательным, а система будет находиться на границе асимптотической устойчивости.

Методы определения устойчивости

Устойчивость линейных систем не зависит от величины возмущения. Система устойчивая при малых возмущениях, будет устойчивой и при больших возмущениях, поэтому достаточно исследовать и определить устойчивость в малом, т.е. найти устойчивость уравнением в форме приращений. Допустим, что в установившемся состоянии регулируемая величина имеет некоторое значение x₀. Выведем систему из этого состояния при помощи какого-либо воздействия, так чтобы x₀ изменилась на . И после этого устраним причину, вызвавшую это изменение, тогда система будет устойчивой, если будет выполняться условие:

(1)

В случае невыполнения этого условия, система будет неустойчивой. Допустим, что изменение регулируемой величины в процессе регулирования. Описывается линейным уравнением n-го порядка с постоянными коэффициентами, тогда отклонение также будет описываться диф.ур. этого порядка. Интегрируя полученное уравнение находим закон изменения интересующей нас переменной по времени, согласно которому можно сделать заключение о характере переходного процесса (устойчивый, неустойчивый). Устойчивость системы определяют характером свободного движения системы, т.к. свободное движение системы описывается однородным диф.ур. (без правой части), то для нахождения условий устойчивости достаточно исследовать св-ва решения однородного диф.ур. В общем случае для системыn-го порядка имеем диф.ур., которое описывает поведение отклонения регулируемой величины:

а₀, а₁, а_n- постоянные коэффициенты, величина которых зависит от параметров САУ.

Решение (2) может быть представлено в виде:

=(3)

A_i- постоянная интегрирования, определяется из начальных условий.

- корни, характеризующие свободное движение и определяемые из характеристического уравнения.

Исследуем (3) с точки зрения устойчивости системы, согласно определению для устойчивости системы необходимо, чтобы отклонение приt, а это возможно только тогда, когда все составляющие уравнения (3) с течением времени стремятся к 0. Поскольку всеA_i=const, то следовательно характер поведения каждой составляющей зависит от. Если- положительное, вещественное число, то составляющаябудет увеличиваться до бесконечности.

При отрицательных вещественных корнях составляющая свободного движения приtмонотонно убывает до 0.

- комплексное число, тогда выражение запишется

(5) – это колебательный процесс, амплитуда А которого возрастает или убывает в зависимости от знака вещественной части комплексного корня. Если>0, то получим колебательный процесс с нарастающей амплитудой. Если<0, то приt, А.

Т.о. аналитические выражения составляющих свободного движения имеют вид:

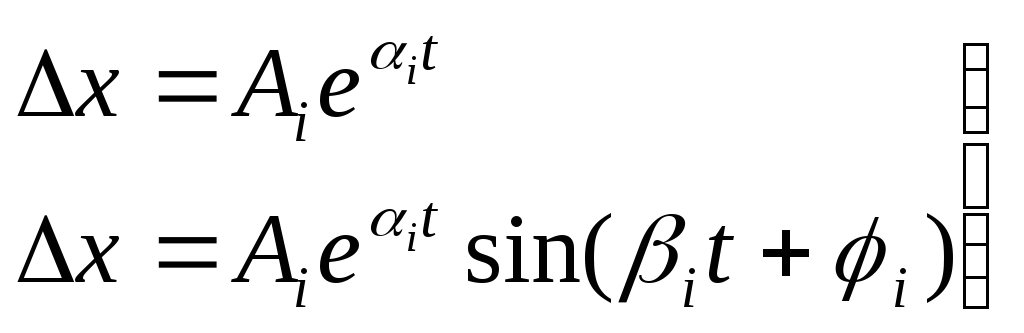(6)

A_i-постоянная интегрирования, определяется из начальных условий.

- вещественная часть корня, характеризующая интенсивность затухания колебаний.

- мнимая часть корня, хар-ся частоту свободных колебаний.

- начальная фаза.