Координати та вектори. Декартові координати на площині

соти вихідної піраміди — центр кола, описаного навколо її основи.

Центр описаної кулі знаходимо так само, як і для повної піраміди.

Вписані кулі

Якщо куля вписана в призму, то в її перпендикулярний переріз можна вписати коло.

Висота призми дорівнює діаметру кола, вписаного

вперпендикулярний переріз призми, тобто діаметру вписаної кулі.

Центр кулі — середина висоти призми, що проходить через центр кола, яке вписане в перпендикулярний переріз.

Центр кулі, яка вписана в пряму призму, — це середина висоти призми, що проходить через центр кола, яке вписане

воснову призми.

Координати та вектори

Декартові координати на площині

Координатна площина

Проведемо дві перпендикулярні координатні прямі, які перетинаються в початку їх відліку — точці О. Ці пря-

Точку О називають п о ч а т к о м к о о р д и н а т. Ці координатні прямі утворюють д е к а р т о в у п р я м о к у т н у с и с т е м у ко о р д и н а т. Площина, на якій задана прямокутна система координат, називається к о о р д и н а т н о ю п л о щ и н о ю. Через будь-яку точку А координатної площини можна провести прямі, перпендикулярні до осей Ox і Oy.

351

Геометрія

Нехай ці прямі перетнуть відповідно вісь абсцис — у точці з координатою а, а вісь ординат — у точці з координатою b.

Пара чисел (а, b) визначає положення точки А на координатній площині й називається її к о о р д и н а т а м и. Позначають А(а, b). Число а називається абсцисою точки А, число b — її ординатою. Зверніть увагу: має значення, у якому порядку записані числа а і b. Точка В(b; а) не збігається з А(а; b).

Якщо точка лежить на осі абсцис, то її ордината дорівнює 0; якщо точка лежить на осі ординат, то її абсциса дорівнює нулю. Початок координат — О(0; 0).

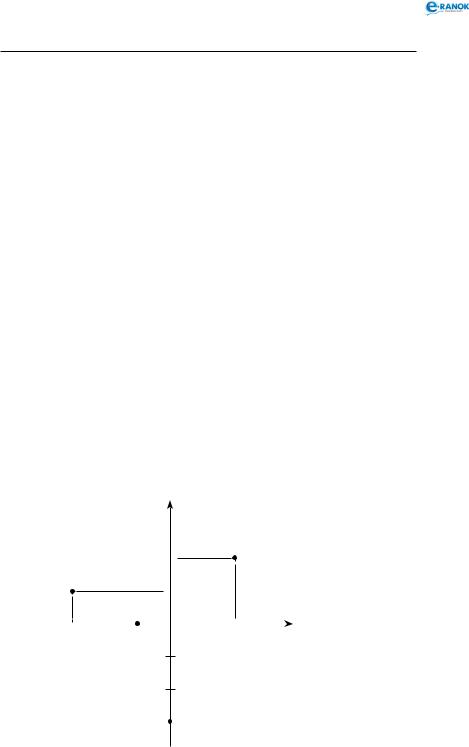
Осі координат розбивають площину на 4 частини, які називаються к о о р д и н а т н и м и ч в е р т я м и. Нумерація чвертей, знаки координат у кожній чверті, а також приклади точок з їх координатами показані на рисунку.

Таким чином, щоб побудувати, наприклад, точку М(k; р), треба поставити олівець в О(0; 0), потім пересунути-

352

Координати та вектори. Декартові координати на площині

Координати середини відрізка

AB = (xA −xB )2 +(yA −yB )2 .

У випадку, коли точка B збігається з початком координат O(0; 0) , отримуємо:

AO = x2A +y2A .

Рівнянням фіг ури на п лощині в декартових ко ординатах називається рівняння з двома змінними x і y, яке задовольняють координати будь-якої точки фігури і тільки вони.

Рівняння кола

(x−a)2 +(y−b)2 = R2 — рівняння кола з центром у точці

A(a; b) і радіусом R. Зверніть увагу:

рівняння x2 +y2 +ax+by+c = 0,

де a2 + b2 −c > 0, задає коло й може бути зведеним до стан-

44

дартного виду.

Рівняння прямої

Будь-яка пряма в декартових координатах x, y має рівняння виду:

ax+ by+ c = 0, де a, b, c — деякі числа.

353

Геометрія

Знаходження координат точки перетину прямих та випадки розміщення прямої відносно системи координат описано в розділі «Алгебра. Лінійна функція».

Рівняння прямої, яка перетинає осі координат в точках (a; 0) і (0; b), де a ≠ 0, b ≠ 0, можна записати у вигляді:

1.Дві прямі паралельні тоді й тільки тоді, коли у них збігаються кутові коефіцієнти, а точки перетину з віссю ординат різні.

2.Кутовий коефіцієнт з точністю до знака дорівнює тангенсу гострого кута, утвореного прямою з віссю абсцис (або дорівнює тангенсу кута між прямою й додатним на-

прямком осі Ox).

3. Прямі, що задані рівняннями y = k1x+b1 і y = k2x+b2, перпендикулярні тоді й тільки тоді, коли k1 k2 = −1.

Означення синуса, косинуса, тангенса, котангенса для будь-якого кута від 0° до 180°

Візьмемо коло на площині Oxy з центром у початку координат і радіусом R.

Відкладемо від додатної півосі Ox кут α у верхню півплощину (див. рисунок нижче). Точку перетину сторони кута з колом назвемо Aα . Вона має координати (x; y).

Тоді sinα = y ;

R

cosα = x ;

R

tgα = y ; x

ctgα = x . y

354