Геометрія

Співвідношення між сторонами й кутами прямокутного трикутника

Нехай ABC — прямокутний трикутник з прямим кутом

Сі гострим кутом при вершині A, що дорівнює α.

Ко с и н у с о м гострого кута прямокутного трикутника називається відношення прилег­ ­лого катета до гіпотенузи.

Значення sinα, cosα, tgα, ctgα залежать тільки від величини кута.

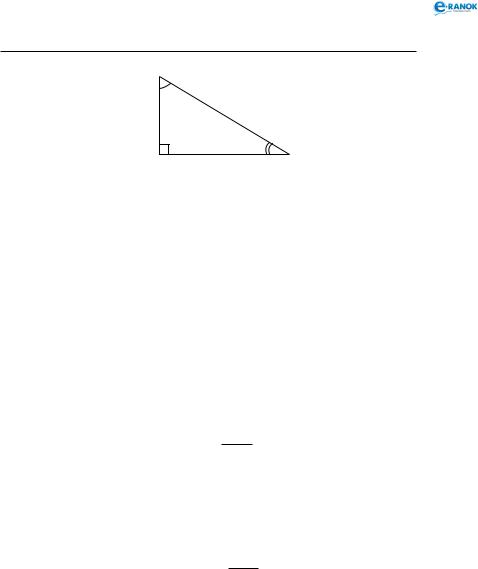
З означень випливає, що для гострих кутів α і β прямокутного трикутника (див. рисунок) маємо:

sinα = cosβ; tgα = ctgβ; cosα = sinβ; ctgα = tgβ;

tgα ctgα =1, а також sinα <1, cosα <1.

254

планіметрія. Трикутники

A α

c

b

β

C a B

Треба вміти знаходити елементи прямокутного трикутника, якщо дані яка-небудь сторона й один із гострих кутів.

Розглянемо такі задачі.

1.Дано: AB = c; A = α (гіпотенуза і гострий кут). Знайти: b; a; β.

Розв’язання:

β = 90°−α;  a = c sinα;  b = c cosα.

2.Дано: AC = b;

A = α (катет і прилеглий кут). Знайти: a; c; β.

Розв’язання:

β = 90°−α;  a = b tgα;  c = b . cosα

3.Дано: BC = a;

A = α (катет і протилежний кут). Знайти: b; c; β.

Розв’язання:

β = 90°−α;  b = a ctgα;  c = a . sinα

Катет, прилеглий до кута α,дорівнює добутку гіпотенузи на cosα.

Катет, протилежний куту α, дорівнює добутку гіпотенузи на sinα.

Катет, протилежний куту α, дорівнює добутку другого катета на tgα.

Основні тригонометричні тотожності, зміну sinα, cosα, tgα при зростанні кута α описано в розділі «Алгебра. Тригонометричні функції».

255

Геометрія

Значення sinα, cosα, tgα, ctgα деяких кутів:

22

Корисним є знання таких співвідношеннь.

1.Катет прямокутного трикутника є середнім пропорційним між гіпотенузою й проекцією цього катета на гіпотенузу.

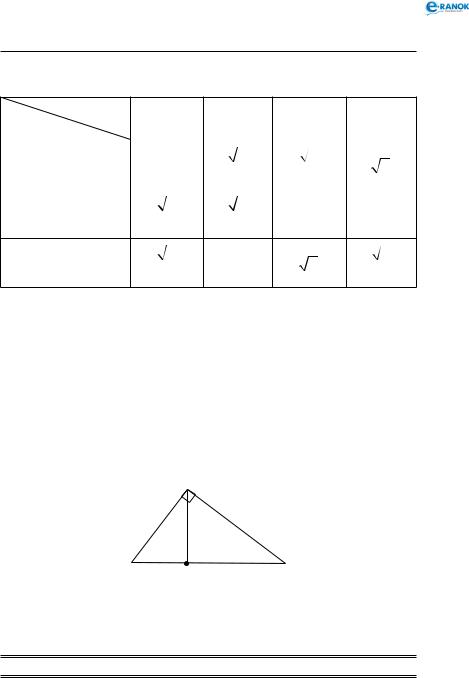
2.Висота прямокутного трикутника, проведена з вершини прямого кута, є середнім пропорційним між проекціями катетів на гіпотенузу.

На рисунку нижче в трикутнику ABC:

AC2 = AD AB; BC2 = DB AB; CD2 = AD DB.

C

A D B

Рух

Якщо кожну точку даної фігури змістити деяким чином, то дістанемо нову фігуру. Кажуть, що ця фігура утворюється перетворенням даної.

256

планіметрія. Рух

Перетворення однієї фігури в іншу називається р у­ х о м, якщо це перетворення зберігає відстані між точками.

Властивості руху

1.Два рухи, виконані послідовно, дають знову рух.

2.Перетворення, обернене до руху, є рух.

3.Під час руху точки, що лежать на прямій, переходять

уточки, які лежать на прямій, і зберігається порядок їх взаємного розміщення.

4.Під час руху прямі переходять у прямі, півпрямі —

упівпрямі, відрізки — у відрізки.

5.Під час руху зберігаються кути між півпрямими.

6.Під час руху паралельні прямі переходять у паралельні прямі.

Симетрія відносно точки

Нехай O — фіксована точка, X — довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок OX′, що дорівнює OX.

Точка X′ називається с и м е т р и ч н о ю т о ч ц і X в і д ­ н о с н о т о ч к и O (див. рисунок).

X′

O

X

Очевидно, що точка, симетрична X′, є точка X. Перетворення фігури F у фігуру F′, при якому кожна

її точка X фігури F переходить у точку X′, симетричну відносно точки O, називається п е р е т в о р е н н я м с и м е ­ т р і ї в і д н о с н о т о ч к и O.

Фігури F і F′ називаються с и м е т р и ч н и м и в і д­ н о с н о т о ч к и O (див. рисунок).

257