
- •Передмова
- •АРИФМЕТИКА
- •Натуральні числа і дії над ними
- •Дії над натуральними числами
- •Числові та буквені вирази
- •Формули
- •Рівняння
- •Звичайні дроби
- •Порівняння звичайних дробів
- •Додавання і віднімання дробів з однаковими знаменниками
- •Додавання і віднімання мішаних чисел з однаковими знаменниками
- •Десяткові дроби
- •Властивості десяткового дробу
- •Дії з десятковими дробами
- •Порівняння та округлення натуральних чисел і десяткових дробів
- •Порівняння
- •Округлення
- •Перетворення звичайного дробу на десятковий і навпаки
- •Середнє арифметичне
- •Відсотки
- •Масштаб
- •Діаграми
- •Числовий промінь
- •Подільність натуральних чисел
- •Дільники і кратні
- •Прості й складені числа
- •Степінь
- •Розкладання числа на прості множники
- •Найменше спільне кратне (НСК)
- •Дії над звичайними дробами
- •Основна властивість дробу
- •Зведення дробів до спільного знаменника
- •Порівняння, додавання та віднімання дробів
- •Перетворення звичайних дробів на десяткові
- •Множення звичайних дробів
- •Взаємно обернені числа
- •Ділення звичайних дробів
- •Основна властивість пропорції
- •Пряма та обернена пропорційність
- •Приклади розв’язування типових завдань
- •Рівняння
- •Задачі на дроби
- •Задачі на рух
- •Комбінаторні задачі
- •Задачі на знаходження частини від числа
- •Задачі на пряму та обернену пропорційність
- •Задачі на пропорційне ділення
- •Задачі на відсотки
- •Задачі на спільну роботу
- •Розв’язування задач за допомогою рівнянь
- •АЛГЕБРА ТА ЕЛЕМЕНТАРНІ ФУНКЦІЇ
- •Дійсні числа
- •Додатні та від’ємні числа
- •Множини чисел
- •Модуль числа
- •Порівняння чисел
- •Дії над дійсними числами
- •Вирази
- •Одночлени
- •Степінь з натуральним показником
- •Одночлен і його стандартний вигляд
- •Многочлени
- •Множення одночлена на многочлен
- •Множення многочлена на многочлен
- •Розкладання многочленів на множники
- •Формули скороченого множення
- •Застосування кількох способів для розкладання многочленів на множники
- •Раціональні вирази
- •Основна властивість дробу. Скорочення дробів
- •Додавання та віднімання дробів
- •Множення, ділення й піднесення до степеня дробів
- •Перетворення раціональних виразів
- •Корені. Ірраціональні вирази
- •Квадратний корень
- •Кoрінь n-го степеня та його властивості
- •Найпростіші перетворення радикалів
- •Узагальнення поняття степеня
- •Основнi означення
- •Властивості степеня з раціональним показником
- •Поняття степеня з ірраціональним показником
- •Логарифм числа
- •Властивості логарифмів
- •Модуль і його властивості
- •Властивості модуля
- •Функції та графіки
- •Лінійна функція
- •Обернена пропорційність
- •Функція y=x2
- •Властивості функцій
- •Перетворення графіків функцій
- •Квадратична функція
- •Екстремуми функції
- •Степенева функція
- •Показникова функція
- •Логарифмічна функція
- •Тригонометричні функції
- •Радіанна система вимірювання кутів і дуг
- •Тригонометричні функції числового аргументу
- •Знаки тригонометричних функцій
- •Періодичність тригонометричних функцій
- •Графіки тригонометричних функцій
- •Властивості тригонометричних функцій
- •Поняття про обернену функцію
- •Рівняння
- •Основні властивості рівнянь
- •Лінійні рівняння з одним невідомим
- •Розв’язування задач за допомогою рівнянь
- •Дробові раціональні рівняння
- •Квадратні рівняння
- •Рівняння, що зводяться до квадратних
- •Розв’язування найпростіших тригонометричних рівнянь
- •Деякі способи розв’язування тригонометричних рівнянь
- •Ірраціональні рівняння
- •Розв’язування логарифмічних рівнянь
- •Розв’язування рівнянь графічним способом
- •Системи рівнянь
- •Лінійне рівняння з двома невідомими
- •Системи лінійних рівнянь з двома невідомими
- •Розв’язування систем рівнянь другого степеня
- •Приклади розв’язування систем тригонометричних рівнянь
- •Нерівності
- •Властивості числових нерівностей
- •НерівностІ з однією змінною
- •Числові проміжки
- •Властивості нерівностей зі змінними
- •Нерівність між середнім арифметичним та середнім геометричним
- •Розв’язування квадратних нерівностей за допомогою графіків
- •Розв’язування найпростіших тригонометричних нерівностей
- •Розв’язування показникових нерівностей
- •Логарифмічні нерівності
- •Системи нерівностей з однією змінною
- •ЕЛЕМЕНТИ МАТЕМАТИЧНОГО АНАЛІЗУ
- •Послідовності
- •Арифметична прогресія
- •Геометрична прогресія
- •Границя
- •Границя числової послідовності
- •Властивості нескінченно малих послідовностей
- •Основні теореми про границі числової послідовності
- •Границя функції
- •Основні теореми про границі функцій
- •Неперервність функції в точці
- •Основні властивості неперервних функцій
- •Метод інтервалів
- •Похідні елементарних функцій
- •Застосування похідної
- •Інтеграл і його застосування
- •Поняття первісної функції
- •Правила знаходження первісних
- •Таблиця первісних
- •Інтеграл
- •КОМБІНАТОРИКА. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ. МАТЕМАТИЧНА СТАТИСТИКА
- •Елементи комбінаторики
- •Початки теорії ймовірностей
- •Основні поняття теорії ймовірностей
- •Вступ до статистики
- •Основні властивості найпростіших геометричних фігур
- •Суміжні й вертикальні кути
- •Властивості суміжних кутів
- •Властивості вертикальних кутів
- •Перпендикуляр
- •Паралельні прямі
- •Бісектриса
- •Висота, бісектриса, медіана трикутника
- •Рівнобедрений трикутник
- •Рівносторонній трикутник
- •Ознаки рівнобедреного трикутника
- •Сума кутів трикутника
- •Прямокутний трикутник
- •Коло
- •Геометричне місце точок
- •Пряма й обернена теореми
- •Доведення від супротивного
- •Приклади розв’язування типових задач
- •Чотирикутники
- •Паралелограм
- •Прямокутник
- •Ромб
- •Квадрат
- •Трапеція
- •Теорема Фалеса
- •Трикутники
- •Середня лінія трикутника
- •Теорема Піфагора
- •Перпендикуляр і похила
- •Нерівність трикутника
- •Співвідношення між сторонами й кутами прямокутного трикутника
- •Властивості руху
- •Симетрія відносно точки
- •Симетрія відносно прямої
- •Поворот
- •Паралельне перенесення та його властивості
- •Співнаправленість півпрямих
- •Властивості перетворення подібності
- •Властивості подібних фігур
- •Кути, пов’язані з колом
- •Кути, вписані в коло
- •Пропорційність відрізків хорд і січних кола
- •Вписані й описані чотирикутники
- •Розв’язування трикутників
- •Теорема косинусів
- •Теорема синусів
- •Розв’язування трикутників
- •Правильні многокутники
- •Довжина кола
- •Площі фігур
- •Площа паралелограма
- •Площа прямокутника
- •Площа ромба
- •Площа квадрата
- •Площа трикутника
- •Площа трапеції
- •Площа чотирикутника
- •Площа круга
- •Площі подібних фігур
- •Аксіоми стереометрії
- •Паралельність прямих і площини
- •Ознака паралельності прямих
- •Ознака паралельності прямої і площини
- •Ознака паралельності площин
- •Властивості паралельних площин
- •Зображення просторових фігур на площині
- •Перпендикулярність прямих і площин
- •Перпендикуляр і похила
- •Теорема про три перпендикуляри
- •Перпендикулярність площин
- •Відстань між мимобіжними прямими
- •Кут між мимобіжними прямими
- •Кут між прямою та площиною
- •Кут між площинами
- •Многогранники
- •Двогранний кут
- •Тригранний і многогранний кути
- •Многогранники
- •Тіла обертання
- •Конус
- •Зрізаний конус
- •Куля
- •Комбінації геометричних тіл
- •Циліндр, вписаний у кулю
- •Циліндр, описаний навколо кулі
- •Конус, вписаний у кулю
- •Куля, вписана в конус
- •Інші комбінації геометричних тіл
- •Описані кулі
- •Вписані кулі
- •Декартові координати на площині
- •Координатна площина
- •Координати середини відрізка
- •Відстань між точками
- •Рівняння кола
- •Рівняння прямої
- •Означення синуса, косинуса, тангенса, котангенса для будь-якого кута від 0° до 180°
- •Вектори на площині
- •Координати векторa
- •Додавання векторів
- •Множення вектора на число
- •Скалярний добуток векторів
- •Розкладання вектора за координатними осями
- •Декартові координати в просторі
- •Перетворення в просторі
- •Подібність просторових фігур
- •Вектори в просторі
- •Предметний покажчик
Алгебра та елементарні функції
а) 2x2 +x−1=1. |
|
|
|
|
|
|
|
|
|
|
|
|
||
2x2 +x−2 = 0, |
|
|
|
|
|
|
|
|
|
|||||
x |
= |
−1± 1+16 |
, |
|
|
|
|
|
|
|
|
|
||
1,2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Відповідь: x1 |
= |
−1+ |
17 |
, |
x2 |
= |
−1− |
17 |
. |
|||||
|
|
|
|
|
|
|||||||||
|
|
|
4 |
|
|
|
|
4 |
|
|
||||
б) 2x2 +x−1=2. |
|
|
|
|
|
|
|
|
|
|
|
|
||
2x2 +x−3 = 0, x |
= |
−1± 1+24 |
, |
|
|
|||||||||
|
|
|
||||||||||||
|
|
|
3,4 |
|
|
|
4 |
|
|
|
|
|
||
x3 =1; x4 = −1,5. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
Відповідь: x1 |
= |
−1+ |
17 |
, |
x2 |
= |
−1− |
17 |
, |
|||||
|
|
|
|
|
|
|||||||||
|
|
|
4 |
|
|
|
|
4 |
|
|
||||
x3 =1, x4 = −1,5.
Розв’язування найпростіших тригонометричних рівнянь
1. cos x = a
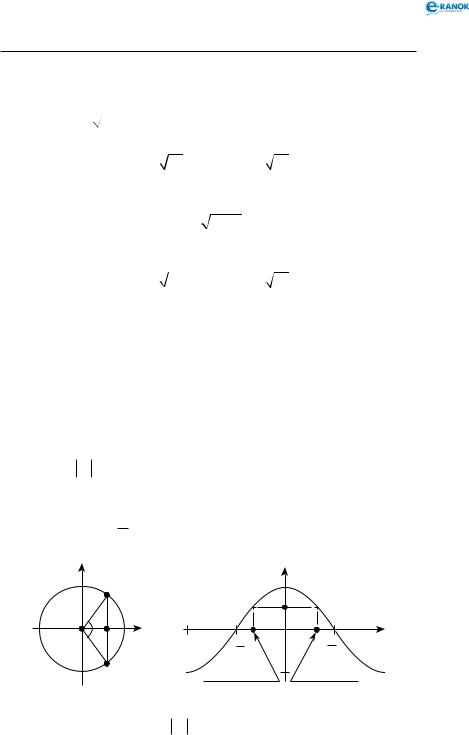
Розв’язки рівняння cosx = a шукатимемо, спираючись на рисунок нижче зліва або на рисунок нижче справа.
Якщо a >1, розв’язків немає.
cosx =1, x =2πn, n Z.
cosx = −1, x = π+2πn, n Z.
cosx = 0, x = π +πn, n Z.
2
y |
arccos a |
|
|
|
a |
O |
x |
|
– arccos a |
y |
1 |
|
|
|
a |
|
|
−π |
|
|
|
− π |
O |
π |
x |
2 |
|
2 |
|
– arccos a |
|
arccos a |
|
Загальнийвипадок ( a <1, a ≠ 0): cosx = a,x=± arccos a+ + 2πn, n Z.
132
Рівняння
У випадках, коли a = 0, a = ±1, теж можна користуватися загальною формулою, але це не так раціонально.
Розв’язки, які описуються загальною формулою, можна поділити на дві серії:
x1 = arccos a + 2πn, n Z; x2 = - arccos a + 2πn, n Z.
2. sin x = a
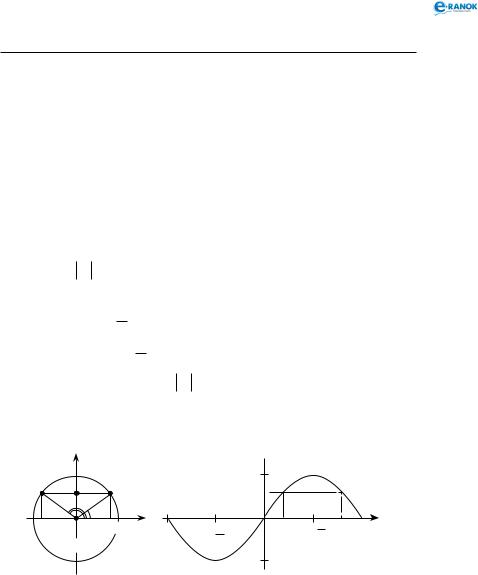
Розв’язки шукатимемо, спираючись на рисунок нижче зліва або на рисунок нижче справа.
Якщо a >1, розв’язків немає.
sinx = 0, x = πn, n Z. sinx =1, x = π +2πn, n Z.
2
sinx = −1, x = − π +2πn, n Z.
2
Загальний випадок ( a <1, a ≠ 0): x = (−1)k arcsina+πk, k Z.
y |
|
|
|
|
|
|
|
a |
|
|
|
arcs |
|
|
arcsina |
−π |
|
|
|
|
|
||
π |
|
O |
x |
|
π |
− |
|
− |
|||
|
in |
|
|
2 |
|
|
a |
|
|
||
|
|
|
|
||
|
|
|
|
|
|
y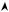
1
a
O
arcsina
π
2
π |
x |
− |
|
arcsin |
|
|
a |
Множина розв’язків розбивається на дві серії:
k = 2n, |
x1 |
= arcsin a + 2πn, |
n Z; |
k = 2n + 1, |
x2 |
= π – arcsin a + 2πn, |
n Z. |
3. tg x = a
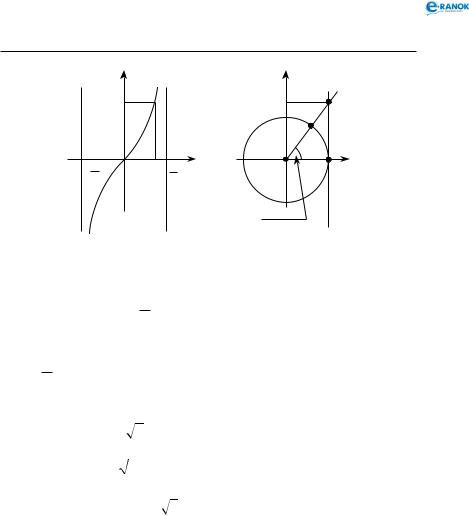
Розв’язки запишемо, спираючись на рисунок нижче зліва або на рисунок нижче справа.
x = arctga+πn, n Z.
133
Алгебра та елементарні функції
|
y |
y |
|
|
a |
a |
|
− π |
O |
|
|
arctg a π x |
O |
x |
22
arctg a
4.ctg x = a
x = arcctga+πn, n Z.
Якщо a = 0, x = π +πn, n Z.
2
Якщо a ≠ 0, можна звести дане рівняння до рівняння
tgx = 1 . a
Приклади
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||
1) 2sin |
|
|
|
|
− |
|
|
|
|
|
= |
3 ; |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
π |
|
|
|
|
x |
|
3 |
|
|
|
|
|
|
|||||||||||||||||||||
sin |
|
|
|
|
− |
|
|
|
|
|
= |
|
|
|
|
|
|
; |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||
|
π |
− |
x |
= |
(−1)k arcsin |
3 |
+πk, k Z; |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||
|
π |
− |
x |
= |
(−1)k |
|
π |
|
+πk, k Z; |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
− |
x |
= (−1)k |
π |
− |
π |
+πk, k Z; |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||
x = (−1)k+1 |
|
4π |
+ |
4π |
−4πk, k Z. |
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|||||||||
Множину розв’язків можна розбити на дві серії: |
|||||||||||||||||||||||||||||||||||||||
x = − |
4π |
+ |
4π |
−4π 2n, n Z; |
|||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x = |
4π |
+ |
4π |
−8πn−4π, n Z; |
|||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
134

Рівняння
x1 = 8πn, n Z;
x2 = − 4π −8πn, n Z.
3
2) cos3xcosx+sin3xsinx = − 2 ;
|
|
|
|
|
|
|
|
2 |
|
cos2x = − |
|
2 |
; |
|
|
|
|||
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
+2πn, n Z; |
||
2x = ±arccos |
− |
|
|||||||
|
|||||||||
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|||
|
π |
|
|
|
|
||||
2x = ± π− |
|
+2πn, n Z; |
|||||||
|
|||||||||
|
4 |
|
|
|
|
||||
2x = ± 3π +2πn, n Z;
4
x = ± 3π +πn, n Z.
8
Деякі способи розв’язування тригонометричних рівнянь
1. Рівняння, що зводяться до квадратних
6cos2 x+5sinx−7 = 0.
cos2 x легко виразити через sin2 x за допомогою основ ної тригонометричної тотожності cos2 x+sin2 x =1:
|
cos2 x =1−sin2 x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Отже, |
|
( |
−sin |
2 |
x |
) |
+5sinx−7 |
= 0 |
; |
|
|||||||||||||
|
|
|
|
6 1 |
|
|
|
|
||||||||||||||||
|
6sin2 x−5sinx+1= 0. |
|
|
|
|
|
||||||||||||||||||
|
Нехай sinx = y, |
|
|
y |
|
1. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
6y2 −5y+1= 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
; |
|
|
|
y2 = |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y1 = 2 |
|
|
|
3 |
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|||||
1) |
sinx = |
1 |
|
; |
x = ( |
−1)k |
+πk, k Z. |
|||||||||||||||||
2 |
|
6 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
x = ( |
−1) |
k |
|
|
|
1 |
+ |
πk, k Z. |
|||||||||
2) |
sinx = |
|
|
; |
|
|
arcsin |
|
|
|
||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||
135

Алгебра та елементарні функції
Відповідь: (−1)k 6π +πk, k Z;
(−1)k arcsin 1 +πk, k Z.
3
2.Спосіб розкладання на множники
1−cos8x = sin4x;
2sin2 4x = sin4x;
sin4x(2sin4x−1) = 0;
sin4x = 0; |
|
|
|
4x = πn, |
n Z; |
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
= (−1) |
k π |
|
|
||||||
|
|
|
|
|
; |
|
|
|
|
|
|
+πk, |
k Z; |
||||||||||
sin4x = |
|
|
|
|
|
|
|
4x |
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|||||
|
πn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
|
, |
|
|
|
n Z; |
|
|
|
|
|
|
|
|
|||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
πk |
|
|
|
|
|
|
|
|
||||
|
(−1) |
k |
|
|
|
+ |
|
|
|
|
k Z. |
|
|
||||||||||
x = |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
||||||||
|
|
24 |
4 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Відповідь: x = |
πn |
, |
n Z; |
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||
x = (−1)k |
π |
+ |
πk |
, k Z. |
|
|
|||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
24 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||
Якщо під час розв’язування одержуємо сукупність кількох серій розв’язків, доцільно перевірити, чи не можна їх описати загальною формулою. Для цього рекомендується використовувати тригонометричне коло:
y 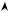
Ox
Наприклад, позначивши на колі дві серії:
x = πn, n Z; |
|||
|
π |
|
|
|
+πk, |
k Z, |
|
x = |
|
||
|
2 |
|
|
136

Рівняння
бачимo, що відповідь можна записати у вигляді x = π +πk,
k Z. |
2 |
|
3.Однорідні рівняння
Узагальному випадку однорідне тригонометричне рівняння має вигляд:
a sinn x+a sinn−1 xcosx+a sinn−2 xcos2 x+…+ |
||
0 |
1 |
2 |
+ a cosn x = 0, де |
a ≠ 0. |
|
n |
|
0 |
Значення x, при яких cosx = 0, не є розв’язком рівнян- |
||
ня. Дійсно, |
якщо |
cosx = 0, рівняння набуде вигляду |
a0 sinn x = 0, звідки sinx = 0. Але sinx і cosx не можуть перетворитися на 0 одночасно.
Із цього випливає, що при діленні обох частин рівняння на cosn x не може відбутися втрата коренів.
Отримуємо: a0 tgn x+a1 tgn−1 x+…+an = 0.
Введемо нову змінну tgx = y і дістанемо алгебраїчне
рівняння: a0yn +a1yn−1 +…+an = 0.
Зверніть увагу: якщо cosk x у лівій частині рівняння можна винести за дужки, то ділення на cosk x веде до втрати коренів.
Приклади
1)5sin2 x+3sinxcosx+4cos2 x =3; 5sin2 x+3sinxcosx+4cos2 x−
−3(sin2 x+cos2 x) = 0;
2sin2 x+3sinxcosx+cos2 x = 0;
2tg2 x+3tgx+1= 0. |
||||||||||
Нехай tgx = y. |
||||||||||
2y2 +3y+1= 0; |
|
|
|
|
|
|
|
|||
y = −1; y = − |
1 |
. |
|
|
|
|
||||
|
||||||||||
1 |
2 |
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
а) |
tgx = −1; |
x = − |
π |
+πn, n Z; |
||||||
|
||||||||||
|
|
|
|
4 |
|
|
|
|||
б) |
tgx = − |
1 |
; |
|
x = −arctg |
1 |
+πn, n Z. |
|||
|
|
|
||||||||
|
2 |
|
2 |
|
||||||
Відповідь: − π +πn, n Z;
4
−arctg |
1 |
+πn, n Z. |
|
||
2 |
|
|
137

Алгебра та елементарні функції
2)sin2 x−sin2x = 0; sin2 x−2sinxcosx = 0;
sinx(sinx−2cosx) = 0;
sinx = 0; |
|
|
x = πn, n Z; |
|
|
|
|
sinx−2cosx = 0; |
|
tgx =2. |
|
x = πn, n Z; |
|
|
|
|
+πn, |
n Z. |
|
x = arctg2 |
|||
Відповідь: x = πn, n Z, x = arctg2+πn, n Z.
4. Спосіб введення допоміжного аргументу
Цей спосіб застосовується для розв’язання рівнянь ви-
ду a sin x + b cos x = c (a > 0).
Поділимо обидві частини рівняння на a2 +b2 . Діста немо:
|
|
a |
|
sinx+ |
|
|
b |
|
|
|
cosx = |
|
|
|
c |
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
a2 + b2 |
|
|
|
a2 + b2 |
|
|
|
|
a2 + b2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Очевидно: |
|
|
|
|
|
|
a |
|
1, |
|
|
|
b |
|
|
1, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
a2 + b2 |
|
|
a2 |
|
+ b2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
a |
|
|
|
2 |
|
|
|
|
b |
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
+ |
|
|
|
|
|
=1. |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
a2 + b2 |
|
a2 + b2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Із цього випливає, що можна ввести до розгляду кут |
||||||||||||||||||||||||||||||||||
ϕ = arctg |
b |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тоді |
|
|
|
|
a |
|
|
= cosϕ; |
|
|
|
|
|
b |
|
|
= sinϕ, і рівняння набуде |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
a2 |
+ b2 |
|
|
|
|
|
|
a2 |
+ b2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
вигляду: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
||||||
cosϕsinx+sinϕcosx = |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
a2 |
+ b2 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
||||||
або sin(x+ϕ) |
= |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 + b2 |
|
|
|
|
|
|
|
|
|||||||||
138

Рівняння
Можна прийняти:
|
a |
|
= sinϕ, |
|
b |
|
= cosϕ. |
|
||||||
|
a2 +b2 |
|
a2 + b2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тоді дістанемо cos(x−ϕ) = |
|
c |
. |
|||||||||||
|
|
|||||||||||||
|
a2 + b2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рівняння |
виду |
|
asinx+ bcosx = c можна розв’язувати |
|||||||||||
і в інший спосіб: |
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
x |
|
|
|
x |
|
|
= c. |
|
|
2asin |
|
cos |
|
|
+b |
|
2cos2 |
|
|
−1 |
|
|||
|
|
|
|
|
|
|||||||||
|
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|
||
Використавши |
тотожність |
cos2 x+sin2 x =1, дістанемо |
||||||||||||
однорідне рівняння. |
|
|
|
|
|
|
|
|||||||
5.Рівняння, що містять тригонометричні функції у знаменнику. Відбір коренів
Ці рівняння зводять до вигляду
f(x) = 0,
розв’язують систему
ϕ(x) ≠ 0.
Приклад
1+ cos2x |
= 0 |
|
cos2x = −1, |
||||
|
|
|
|||||
1+ sinx |
|
|
sinx ≠ −1. |
||||
|
π |
|
|
|
|
|
|
x = |
|
|
+πn, n Z, |
||||
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
||
|
|
|
|
|
|
||
x ≠ − |
|
|
|
+2πk, |
k Z. |
||
|
|
|
|||||
|
|
|
2 |
|
|
|
|
f (x) |
= 0, а потім |
ϕ(x) |
Відбір коренів зручно виконувати, скориставшись тригонометричним колом.
Позначимо на колі точки, що відповідають кутам виду
π + πn, n Z.
2
Потім відкинемо (виколемо) ті з них, які мають вигляд
−π +2πk, k Z (див. рисунок нижче).
2
139
Алгебра та елементарні функції
sin x 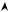
Ocos x
Відповідь: π + 2πn, n Z.
2
6.Випадок, коли треба знайти тільки певні розв’язки
Приклад. Скільки розв’язків рівняння
sin2 3x+ sin2 5x = 1 належать проміжку
sin2 3x+ sin2 5x = 1;
1−cos6x + 1−cos10x = 1;
22
1−cos6x+1−cos10x =2; cos6x+cos10x = 0; 2cos8xcos2x = 0;
|
π |
? |
|
0; |
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
cos8x = |
0; |
|
8x = |
|
+ πn, |
n Z; |
||||||||
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0. |
|
|
π |
|
|
||||
cos2x = |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2x = |
|
|
+ πk, |
n Z. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
π |
|
|
|
|
πn |
|
|
|
|
|
|
||
x = |
|
|
|
+ |
|
|
|
, |
n Z; |
|
|
|
||
16 |
8 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||
π |
|
|
πn |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
x = |
|
|
+ |
|
|
|
, |
|
n Z. |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
|
4 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Треба відповісти на запитання, скільки розв’язків нале-
|
π |
|
жить проміжку 0; |
|
. |
|
||
|
2 |
|
I c по сіб. Розглянемо нерівності:
1) 0 |
π |
+ |
πn |
|
π |
; |
2) 0 |
π |
+ |
πn |
|
π |
; |
|
|
|
|
|
|
|
|||||||||
16 |
8 |
|
|
2 |
|
4 |
|
2 |
2 |
|
||||
0 1+2n 8; |
|
|
0 1+2n 2; |
|||||||||||
140
