В частном случае прямой линии и постоянного тока получаем закон Эрстеда [28, с. 216; 31; 41]
|
|
|
|
= |
|
|
|
|
|
|
|
|
(105) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
вектор в |
|
|
|
|
|
|
|
|
|
|
– рас- |
|||
как следствие уравнений движения эфира (4)–(6). Здесь |
|
|||||||||||||
стояние от прямой |
|
до рассматриваемой точки, |
|
– |
единичный |
|||||||||
|
|
|
|
|
|
|
||||||||
|
цилиндрической системе координат |
|
|
|
|
с осью |
, |
|||||||
совпадающей с прямой |
. Внутри провода |
магнитное поле имеет |
||||||||||||
|
|
( , , ) |
|
|
|
|
||||||||
другую зависимость от радиуса (287), не содержащую особен- |
||||||||||||||
ность. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отметим, что знание поля , рассчитанного, например, |
по |
|||||||||||||
необходимо привлечь |
|
|
|
|
с помощью (20) |
|||||||||
формуле (105) или |
аналогичным ей, позволяет |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
найти произведение |
|
. Для определения |
|
и |
|
по отдельности |
||||||||
|
|
|
ещё уравнения (22), (23), (15). |
|
|
|
|
|
||||||
Уравнение Максвелла (102) и закон Био – Савара (103), (104) |
||||||||||||||
устанавливают тесную взаимосвязь в эфире между вектором |
|||||||||||||||||
наличии |
с |
× |
(| | |
2 |
|
|
2 |
) ≠ 0 |
, согласно |
|
total |
|
|||||
протекать |
|
|
/ |
|
|
|
|
|
|
|
|
, а именно: при |
|||||
магнитной индукции |
|
и плотностью тока |
|
||||||||||||||
эфире должно total |
|
|
|
|
|
|
|
|
total |
|
(102), в эфире должен |
||||||
|
ток |
|
, а при наличии |
|
|
, согласно (103), (104), в |
|||||||||||
|
|
иметься магнитное поле |
|
. Важно подчеркнуть, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
total |
|
|||
что присутствие заряженных частиц |
при этом не обязательно. |
||||||||||||||||
|
|
|
|
|
|||||||||||||
Вся взаимосвязь |
|
и плотности тока |
|
|
|
определяется только |
|||||||||||
соответствующими плотностью |
|
и скоростью эфира. |
|||||||||||||||
8.Индуктивность геометрического объекта, создающего магнитное поле
Впостановке задачи с постоянной плотностью эфира существует простая связь между магнитным потоком через контур,
125
общем случае. |
|
|
|
|
|
|
|
( ) |
[41]. Установим эту связь в |
|||||||||||||||||||||||
ограничивающий поверхность |
|
|
|
|||||||||||||||||||||||||||||
ляется |
|
|
Φ |
магнитного поля |
через поверхность |
( ) |
опреде- |
|||||||||||||||||||||||||
|
Поток |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
поверхностным интегралом второго рода |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
( ) |
Φ( ) ≡ ( ) ( , ) ∙ ( , ) . |
|
|
|
|
|
|
|
|
|
|
|
(106) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Φ |
|
|
|
|
|
|
|
|
|
|
, так как для за- |
|||||||||
Здесь рассмотрим незамкнутую поверхность |
|
|
|
|
||||||||||||||||||||||||||||
мкнутой |
|
|
|
магнитный поток |
|
|
равен |
нулю в силу теоремы |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|||||||||||||||||
один и тот же контур, не влияет на |
|
|
( ) |
|
|
|
|
|
|
|
(27). |
|
||||||||||||||||||||
Остроградского – Гаусса и соленоидальности поля |
|
|
||||||||||||||||||||||||||||||
|
Форма |
незамкнутой |
|
поверхности |
|
|
|
|
, |
опирающейся на |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
следует из равенства |
|
|
|
|
|
|
|
значение |
Φ |
. Это утверждение |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Φ( ) − |
Φ1( ) = ( ) ∙ − 1( ) ∙ = |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
( ) ∙ |
+ 1( ) ∙ |
(− ) = |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
( ) 1( ) |
∙ = ( ) ∙ = 0, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
тур, что1( )и |
|
|
. Нормаль в интеграле по |
по1( ) |
берётся с той же |
|||||||||||||||||||||||||||
стороны поверхности( ) |
, что и в интеграле |
|
|
. Поэтому нор- |
||||||||||||||||||||||||||||
где |
|
|
– произвольная поверхность, натянутая на тот же кон- |
|||||||||||||||||||||||||||||
ней нормали, |
|
|
|
1( ) |
|
|
|
|
|
|
|
|
|
переходев нём квнеш- |
||||||||||||||||||
мальвинтегралепо |
|
|
меняетзнакпри |
|
|
|
( ) |
|
total |
|
|
|
||||||||||||||||||||
по кривой |
|
|
. На данном |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||
|
|
|
|
|
|
фигурирующей в интеграле по |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
не связана с( поверхностью) |
|
|
|
. Кроме того, в |
|
|
|
( ) |
|
|||||||||||||||||||||||
|
Пусть магнитное поле |
|
|
индуцируется |
током |
|
|
, текущим |
||||||||||||||||||||||||
|
|
|
|
|
( ) |
|
1( ) |
|
||||||||||||||||||||||||
претации кривая |
|
|
не |
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
никак |
||||||||
|
|
|
|
|
|
|
( ) |
|
|
этапе рассуждений кривая |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
126 |
|
|
|
|
|
|
|
|
|
эфирной интер- |
||||||||||
обязательно должна совпадать с каким-
то материальным носителем, например с металлическим проводником.
Подставим эфирный аналог формулы Био – Савара для нити (104) в определение (106)
|
|
|
Φ = ( ) |
|
| |2 ( ) total |
3 |
|
∙ . |
|
|
|
|
|
||||||||||
В |
случае, когда в точках кривой |
( ) |
ток одинаков |
total = |
|||||||||||||||||||
|
, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
total( ) |
|
|
Φ = |
2 |
total |
|
|
|
, |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
(107) |
|||||||||||
|
|
|
|
|
|
|
|
|
( ) |
× |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
( ) ≡ ( ) | |2 |
3 |
|
∙ . |
|
|
|
|
|
|||||||||||
Если в качестве кривой |
|
выбрать контур, ограничиваю- |
|||||||||||||||||||||
щий незамкнутую |
поверхность |
|
, |
и рассмотреть |
|
|
|
, то |
|||||||||||||||
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
как пока- |
||||||||
|
будет зависеть только от геометрии( ) |
кривой |
|
|
|||||||||||||||||||
|
|
|
| | |
≈ |
|
||||||||||||||||||
зано выше, не зависит от формы |
|
|
|
|
). Поэтому |
|
|
в фор- |
|||||||||||||||
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
можно рассматривать как эфирное обобщение клас- |
|||||||||||||||||||
муле (107) |
Φ |
|
|
|
|
|
|
|
|
( ) |
|
|
|
( ) |
|
|
|||||||
сического понятия индуктивности тонкого замкнутого тока.
( )
также называют самоиндукцией, или коэффициентом самоиндукции (см., например: [28, с. 271]).
Применяя( ) выражение (100) в определении магнитного потока (106), можно аналогично ввести понятие индуктивности объёма , создающего магнитное поле .
9.Основной закон электромагнитной индукции. Электродвижущая сила. Правило Ленца
Рассмотрим производную по времени от магнитного потока (106) в общем виде, в отличие от упрощённого подхода [41],
127
|
= |
( ) ∙ . |
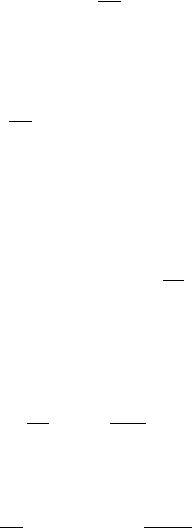
Всоответствии с эфирным представлением магнитного поля
(20)и формулой Стокса, имеем
|
|
= ( ) × ( ) ∙ |
= |
( ) ∙ , |
(108) |
|||||||||||||||||
хода |
) |
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|||
|
В ([ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, направление об- |
|||||
где контур |
|
|
ограничивает поверхность |
|
||||||||||||||||||
|
|
|
|
определяется по вектору |
|
правым винтом. |
|
|||||||||||||||
|
21] на с. 152 или в [35] на с. 4 3 выведено интегральное |
|||||||||||||||||||||
тождество |
|
|
|
|
|
|
|
|
− × ( × ) ∙ , |
|
|
|||||||||||
|
|
( ) ∙ = ( ) |
|
( ) |
|
|||||||||||||||||
где |
= ( , ) |
– скорость движения точек контура |
, ограни- |
|||||||||||||||||||
|
Применим эту |
|
|
( ) |
. |
|
|
= |
|
|
|
|
|
|||||||||
чивающего поверхность |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
формулу для |
|
|
|
|
: |
|
|
|
|
|||||
|
|
|
= ( ) |
|
− × × ( ) ∙ |
. |
|
|
||||||||||||||
|
Воспользуемся уравнением (24) и определением (20) |
|||||||||||||||||||||
|
|
= ( ) − + |
,0 |
|
− × ( × ) ∙ . |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
128 |
|
|
|
|
|
|
|
|
|
Учитывая),, получаем |
|
|
|
|
|||||
× ( ) = 0 |
что член |
|
не вносит вклад в интеграл (так как |
||||||
|
|
||||||||
( ) ≡ |
|
|
= −( ), |
|
∙ . |
(109) |
|||
|
|
+ × − |
|
||||||
|
( ) |
( ) |
|
|
|
,0 |
|
|
|
(э.д.с. |
называетсяэлектродвижущейсилойиндукции |
||||||||
Функция |
|
||||||||
индукции), а формула (109) – основным законом электромагнитной индукции (см., например: [28, c. 258]). В отличие от классической физики, здесь этот закон получен не как обобщение опытов, а как формальное математическоеследствиеуравнений движения эфира (4)–(6), то есть уравнения неразрывности и второго закона Ньютона.
Подчеркнём, что формулы (108) и (109) показывают, что э.д.с. индукции появляется в контуре при изменении магнитного поля или контура во времени, а( также) в присутствии электрического поля. Причём вклад в даёт только непотенциальная составляющая вектора , так как интеграл по замкнутому контуру от потенциальной составляющей равен нулю.
Физическая трактовка второго (магнитного) члена под интегралом в формуле (109) дана в п. 18.11.
Рассмотренная э.д.с. индукции является лишь одним из способов возбуждения э.д.с. Существуют и другие способы генерации э.д.с., не связанные с изменением магнитного поля или изменением контура. Например, э.д.с. может возникать при создании разности потенциалов на участке неподвижного контура за счёт электрической батареи или действия внешней силы. Каждыйспособгенерацииэ.д.с.описывается,вообщеговоря, своими количественными соотношениями.
Правило Ленца в физике установлено обобщением опытных фактов: индукционный ток всегда имеет такое направление, что
129
он ослабляет действие причины, возбуждающей этот ток (см., например: [28, c. 260]). В эфирной интерпретации это правило также является формальным следствием уравнений эфира, а
именно формулы (109). |
|
|
|
|
|
|||||
можно |
|
|
|
|
|
|
|
выражается |
||
С помощью формул (20), (21) э.д.с. индукции |
|
|||||||||
через плотность |
|
и скорость эфира. Поэтому |
формулу (109) |
|||||||
|
|
|
|
|
||||||
|
интерпретировать как возникновение э.д.с. индукции в |
|||||||||
результате движения эфира в замкнутом контуре |
|
, вызван- |
||||||||
совпадает с |
|
|
( ) |
|
|
|
|
этим |
||
ного изменением магнитного потока через ограниченную( ) |
||||||||||
контуромповерхность |
|
.Отсюдаследует,что,например,если |
||||||||
воднике( ) |
|
проводником, то электрический ток в этом про- |
||||||||
обусловлен в первую очередь движением в нём эфира, а |
||||||||||
не движением заряженных частиц. Движение заряженных частиц обусловлено потоком эфира. Данный результат позволяет сделать важный для практики вывод: э.д.с. можно возбуждать,используя имеющееся в природе движение эфира со скоростью
.
Более подробно электрический ток в проводниках рассмотрен в п. 12 и 18.
В общей физике возбуждение и течение электрического тока при движении проводника в магнитном поле связываются исключительно с движением в нём электронов [28, 31, 34], а механизм действия на них силы Лоренца объясняется релятивистским эффектом [32, т. 3, с. 72; 28, с. 16]. При этом возникают большие проблемы с интерпретацией многих опытов. Например, эксперименты показывают, что в длинном проводнике постоянный ток, возбуждённый на одном из его концов, появляется на другом конце значительно быстрее характерного времени направленного движения заряженных частиц в нём (если такие есть). Высокую скорость передачи сигналов по проводнику труднообъяснитьспомощьюэлектронов,скоростьдвижениякоторыхдляметалловсоставляетнеболеенесколькихсантиметров в секунду, а для электролитов ещё меньше (см., например: [28, с.
130