
- •Передмова
- •АРИФМЕТИКА
- •Натуральні числа і дії над ними
- •Дії над натуральними числами
- •Числові та буквені вирази
- •Формули
- •Рівняння
- •Звичайні дроби
- •Порівняння звичайних дробів
- •Додавання і віднімання дробів з однаковими знаменниками
- •Додавання і віднімання мішаних чисел з однаковими знаменниками
- •Десяткові дроби
- •Властивості десяткового дробу
- •Дії з десятковими дробами
- •Порівняння та округлення натуральних чисел і десяткових дробів
- •Порівняння
- •Округлення
- •Перетворення звичайного дробу на десятковий і навпаки
- •Середнє арифметичне
- •Відсотки
- •Масштаб
- •Діаграми
- •Числовий промінь
- •Подільність натуральних чисел
- •Дільники і кратні
- •Прості й складені числа
- •Степінь
- •Розкладання числа на прості множники
- •Найменше спільне кратне (НСК)
- •Дії над звичайними дробами
- •Основна властивість дробу
- •Зведення дробів до спільного знаменника
- •Порівняння, додавання та віднімання дробів
- •Перетворення звичайних дробів на десяткові
- •Множення звичайних дробів
- •Взаємно обернені числа
- •Ділення звичайних дробів
- •Основна властивість пропорції
- •Пряма та обернена пропорційність
- •Приклади розв’язування типових завдань
- •Рівняння
- •Задачі на дроби
- •Задачі на рух
- •Комбінаторні задачі
- •Задачі на знаходження частини від числа
- •Задачі на пряму та обернену пропорційність
- •Задачі на пропорційне ділення
- •Задачі на відсотки
- •Задачі на спільну роботу
- •Розв’язування задач за допомогою рівнянь
- •АЛГЕБРА ТА ЕЛЕМЕНТАРНІ ФУНКЦІЇ
- •Дійсні числа
- •Додатні та від’ємні числа
- •Множини чисел
- •Модуль числа
- •Порівняння чисел
- •Дії над дійсними числами
- •Вирази
- •Одночлени
- •Степінь з натуральним показником
- •Одночлен і його стандартний вигляд
- •Многочлени
- •Множення одночлена на многочлен
- •Множення многочлена на многочлен
- •Розкладання многочленів на множники
- •Формули скороченого множення
- •Застосування кількох способів для розкладання многочленів на множники
- •Раціональні вирази
- •Основна властивість дробу. Скорочення дробів
- •Додавання та віднімання дробів
- •Множення, ділення й піднесення до степеня дробів
- •Перетворення раціональних виразів
- •Корені. Ірраціональні вирази
- •Квадратний корень
- •Кoрінь n-го степеня та його властивості
- •Найпростіші перетворення радикалів
- •Узагальнення поняття степеня
- •Основнi означення
- •Властивості степеня з раціональним показником
- •Поняття степеня з ірраціональним показником
- •Логарифм числа
- •Властивості логарифмів
- •Модуль і його властивості
- •Властивості модуля
- •Функції та графіки
- •Лінійна функція
- •Обернена пропорційність
- •Функція y=x2
- •Властивості функцій
- •Перетворення графіків функцій
- •Квадратична функція
- •Екстремуми функції
- •Степенева функція
- •Показникова функція
- •Логарифмічна функція
- •Тригонометричні функції
- •Радіанна система вимірювання кутів і дуг
- •Тригонометричні функції числового аргументу
- •Знаки тригонометричних функцій
- •Періодичність тригонометричних функцій
- •Графіки тригонометричних функцій
- •Властивості тригонометричних функцій
- •Поняття про обернену функцію
- •Рівняння
- •Основні властивості рівнянь
- •Лінійні рівняння з одним невідомим
- •Розв’язування задач за допомогою рівнянь
- •Дробові раціональні рівняння
- •Квадратні рівняння
- •Рівняння, що зводяться до квадратних
- •Розв’язування найпростіших тригонометричних рівнянь
- •Деякі способи розв’язування тригонометричних рівнянь
- •Ірраціональні рівняння
- •Розв’язування логарифмічних рівнянь
- •Розв’язування рівнянь графічним способом
- •Системи рівнянь
- •Лінійне рівняння з двома невідомими
- •Системи лінійних рівнянь з двома невідомими
- •Розв’язування систем рівнянь другого степеня
- •Приклади розв’язування систем тригонометричних рівнянь
- •Нерівності
- •Властивості числових нерівностей
- •НерівностІ з однією змінною
- •Числові проміжки
- •Властивості нерівностей зі змінними
- •Нерівність між середнім арифметичним та середнім геометричним
- •Розв’язування квадратних нерівностей за допомогою графіків
- •Розв’язування найпростіших тригонометричних нерівностей
- •Розв’язування показникових нерівностей
- •Логарифмічні нерівності
- •Системи нерівностей з однією змінною
- •ЕЛЕМЕНТИ МАТЕМАТИЧНОГО АНАЛІЗУ
- •Послідовності
- •Арифметична прогресія
- •Геометрична прогресія
- •Границя
- •Границя числової послідовності
- •Властивості нескінченно малих послідовностей
- •Основні теореми про границі числової послідовності
- •Границя функції
- •Основні теореми про границі функцій
- •Неперервність функції в точці
- •Основні властивості неперервних функцій
- •Метод інтервалів
- •Похідні елементарних функцій
- •Застосування похідної
- •Інтеграл і його застосування
- •Поняття первісної функції
- •Правила знаходження первісних
- •Таблиця первісних
- •Інтеграл
- •КОМБІНАТОРИКА. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ. МАТЕМАТИЧНА СТАТИСТИКА
- •Елементи комбінаторики
- •Початки теорії ймовірностей
- •Основні поняття теорії ймовірностей
- •Вступ до статистики
- •Основні властивості найпростіших геометричних фігур
- •Суміжні й вертикальні кути
- •Властивості суміжних кутів
- •Властивості вертикальних кутів
- •Перпендикуляр
- •Паралельні прямі
- •Бісектриса
- •Висота, бісектриса, медіана трикутника
- •Рівнобедрений трикутник
- •Рівносторонній трикутник
- •Ознаки рівнобедреного трикутника
- •Сума кутів трикутника
- •Прямокутний трикутник
- •Коло
- •Геометричне місце точок
- •Пряма й обернена теореми
- •Доведення від супротивного
- •Приклади розв’язування типових задач
- •Чотирикутники
- •Паралелограм
- •Прямокутник
- •Ромб
- •Квадрат
- •Трапеція
- •Теорема Фалеса
- •Трикутники
- •Середня лінія трикутника
- •Теорема Піфагора
- •Перпендикуляр і похила
- •Нерівність трикутника
- •Співвідношення між сторонами й кутами прямокутного трикутника
- •Властивості руху
- •Симетрія відносно точки
- •Симетрія відносно прямої
- •Поворот
- •Паралельне перенесення та його властивості
- •Співнаправленість півпрямих
- •Властивості перетворення подібності
- •Властивості подібних фігур
- •Кути, пов’язані з колом
- •Кути, вписані в коло
- •Пропорційність відрізків хорд і січних кола
- •Вписані й описані чотирикутники
- •Розв’язування трикутників
- •Теорема косинусів
- •Теорема синусів
- •Розв’язування трикутників
- •Правильні многокутники
- •Довжина кола
- •Площі фігур
- •Площа паралелограма
- •Площа прямокутника
- •Площа ромба
- •Площа квадрата
- •Площа трикутника
- •Площа трапеції
- •Площа чотирикутника
- •Площа круга
- •Площі подібних фігур
- •Аксіоми стереометрії
- •Паралельність прямих і площини
- •Ознака паралельності прямих
- •Ознака паралельності прямої і площини
- •Ознака паралельності площин
- •Властивості паралельних площин
- •Зображення просторових фігур на площині
- •Перпендикулярність прямих і площин
- •Перпендикуляр і похила
- •Теорема про три перпендикуляри
- •Перпендикулярність площин
- •Відстань між мимобіжними прямими
- •Кут між мимобіжними прямими
- •Кут між прямою та площиною
- •Кут між площинами
- •Многогранники
- •Двогранний кут
- •Тригранний і многогранний кути
- •Многогранники
- •Тіла обертання
- •Конус
- •Зрізаний конус
- •Куля
- •Комбінації геометричних тіл
- •Циліндр, вписаний у кулю
- •Циліндр, описаний навколо кулі
- •Конус, вписаний у кулю
- •Куля, вписана в конус
- •Інші комбінації геометричних тіл
- •Описані кулі
- •Вписані кулі
- •Декартові координати на площині
- •Координатна площина
- •Координати середини відрізка
- •Відстань між точками
- •Рівняння кола
- •Рівняння прямої
- •Означення синуса, косинуса, тангенса, котангенса для будь-якого кута від 0° до 180°
- •Вектори на площині
- •Координати векторa
- •Додавання векторів
- •Множення вектора на число
- •Скалярний добуток векторів
- •Розкладання вектора за координатними осями
- •Декартові координати в просторі
- •Перетворення в просторі
- •Подібність просторових фігур
- •Вектори в просторі
- •Предметний покажчик
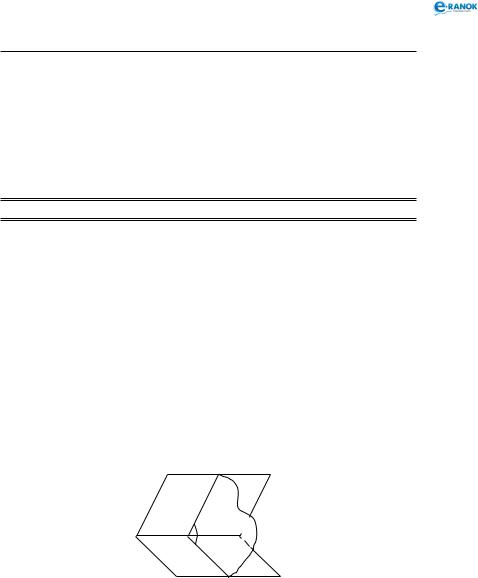
Стереометрія. Многогранники
Теорема. Площа ортогональної проекції многокутника на площину дорівнює добутку його площі на косинус кута між площиною многокутника і площиною проекції.
Многогранники
Двогранний кут
Д в о г р а н н и м к у т о м називається фігура, утворена двома півплощинами зі спільною прямою, що їх обмежує, —
р е б р о м |
двогранного кута. Півплощини називаються |
г р а н я м и |
двогранного кута. |
Площина, перпендикулярна до ребра двогранного кута, перетинає його грані по двох півпрямих. Кут, утворений такими півпрямими, називається л і н і й н и м к у т о м двогранного кута (див. рисунок). За міру двогранного кута приймається міра його лінійного кута.
αa
ϕ  γ
γ
βb
Міра двогранного кута не залежить від вибору лінійного кута.
Побудувати лінійний кут двогранного кута можна двома способами.
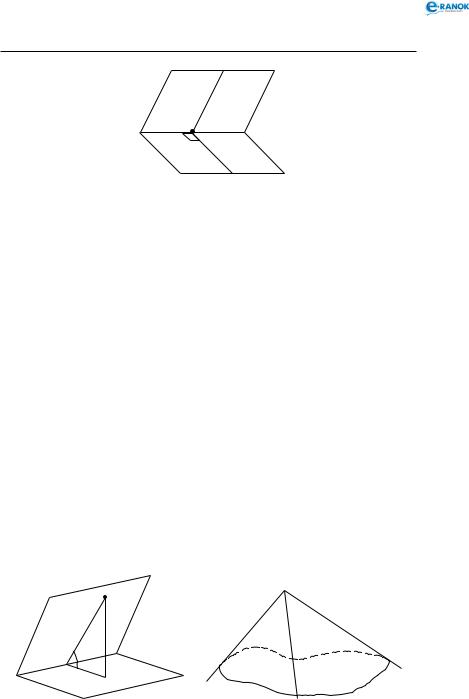
1.Обрати точку на ребрі кута й провести через цю точку перпендикуляри до ребра, що лежать у гранях кута (див. рисунок). Кут між цими перпендикулярами — лінійний кут даного двогранного кута.
315
Геометрія
αa
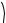 ϕ c
ϕ c
βb
2.Обрати точку на грані двогранного кута й опустити з неї перпендикуляри на ребро кута та на іншу грань двогранного кута (див. рисунок нижче ліворуч). З’єднати основи цих перпендикулярів. Кут між цим відрізком
іперпендикуляром, проведеним до ребра двогранного кута, буде лінійним кутом даного двогранного кута.
Тригранний і многогранний кути
Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині.
Тр и г р а н н и м к у т о м (abc) називається фігура, яка
складається з трьох плоских кутів (ab), |
(bc) , (ac) |
(див. |
рисунок праворуч). Ці кути називаються |
г р а н я м и |
три- |
гранного кута, а їх сторони — р е б р а м и. Спільна вершина плоских кутів називається в е р ш и н о ю тригранного кута. Двогранні кути, утворені гранями тригранного кута,
називаються д в о г р а н н и м и к у т а м и т р и г р а н н о г о к у т а. Аналогічно дають означення м н о г о г р а н н о г о к у т а.
|
|
S |
|
α |
A |
|
|
|
c |
ϕ |
c |
|
a |
|
|
|
|
|
β |
b |
Теорема 1. У тригранному куті кожний плоский кут менший за суму двох інших.
316
Стереометрія. Многогранники
Теорема 2. Сума плоских кутів тригранного кута менша за 360° .
Многогранники
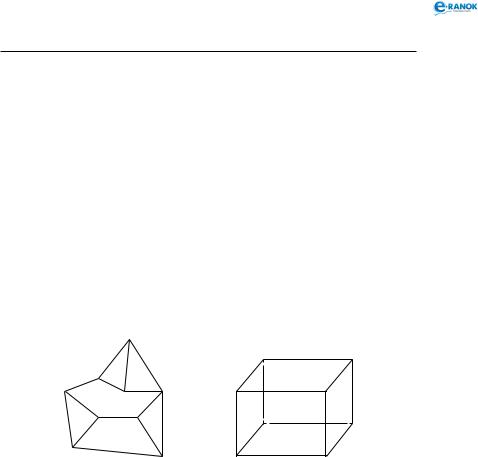
Мн о г о г р а н н и к — це таке тіло, поверхня якого складається із скінченної кількості плоских многокутників. Многогранник називається о п у к л и м, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні. Спільна частина такої площини й поверхні опуклого многогранника називається г р а н н ю.
На рисунку нижче зліва зображений неопук лий многогранник; на рисунку справа — опуклий.
Грані опуклого многогранника є плоскими опуклими многокутниками. Сторони граней називаються р е б р а м и
мн о г о г р а н н и к а, а вершини граней — в е р ш и н а м и
мн о г о г р а н н и к а.
Призма
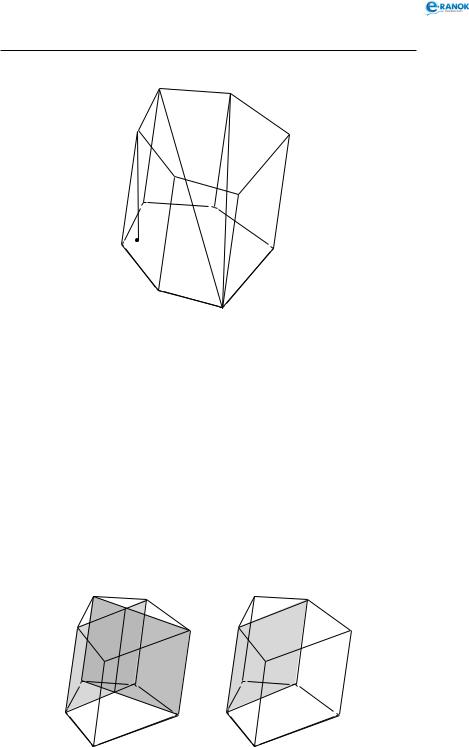
П р и з м о ю називається многогранник, який складається з двох плоских многокутників, що лежать у різних площинах і суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих многокутників (див. рисунок). Многокутники називаються о с н о в а м и п р и з м и, а відрізки, які сполучають відпо-
відні вершини, — б і ч н и м и р е б р а м и п р и з м и.
317
ГеОмеТрія
|
|
B1 |
C1 |
|
|
|
|
|
A1 |
|
D1 |
|
|
|
|
|
|
F1 |
|
|
|
B |
C E1 |
|
|
|
|
A |
|
N |
D |
|
|
||
|
|
|
|
|
|
F |
|
|
|
|
E |
Позначення: ABCDEFA1B1C1D1E1F1.
Бічна поверхня призми складається з паралелограмів. Кожний із них має дві сторони, які є відповідними сторонами основ, а дві інші — суміжними бічними ребрами. Основи призми рівні й лежать у паралельних площинах. Бічни ребра призми паралельні та рівні. В и с о т о ю п р и з м и називається відстань між площинами її основ.
Відрізок, який сполучає дві вершини призми, що не належать одній грані, називається д і а г о н а л л ю п р и з м и. (На рисунку A1N — висота, B1E і C1E — діагоналі.)
Д і а г о н а л ьн і п е р е р і з и — це перерізи призми пло-
щинами, що проходять через два бічних ребра, які не належать одній грані (див. рисунки).
318

Стереометрія. Многогранники
Призма називається п р я м о ю, якщо її бічні ребра перпендикулярні до основ. У протилежному випадку призма називається п ох и л о ю.
Бічні грані прямої призми — прямокутники, висота прямої призми дорівнює бічному ребру, діагональні пере-
різи є прямокутниками |
. |
|
|
Б і ч н о ю п о в е р х н е ю |
призми називається |
сума |
|
площ бічних граней. П о в н а |
п о в е р х н я п р и з м и |
до- |
|
рівнює сумі бічної поверхні й площ основ.
Теорема 1. Бічна поверхня прямої призми дорівнює добутку периметра основи на висоту, тобто на довжину бічного ребра.
П е р п е н д и к у л я р н и м п е р е р і з о м п р и з м и бу-
демо називати переріз площиною, перпендикулярною до бічного ребра призми (а це означає, що ця площина є перпендикулярною до всіх бічних ребер призми).
Теорема 2. Бічна поверхня похилої призми дорівнює добутку довжини бічного ребра на периметр перпендикулярного перерізу.
На рисунку ABC — перпендикулярний переріз.
Sб = H Pосн; |
|
|
Sп = Sб + 2Sосн. |
|
C |
Sб = l Pпер; |
|
|
Sп = Sб + 2Sосн. |
A |
l |
|
|
B |
Очевидно, що ця теорема є правильною й у випадку прямої призми, бо тоді перпендикулярний переріз буде перерізом площиною, паралельною площинам основ призми.
Зверніть увагу: якщо деякий многокутник є перпендикулярнимперерізомпризми,тойоговнутрішнікутиєлінійними кутамидвограннихкутівміжвідповіднимибічнимигранями.
Увипадкупрямоїпризмилінійнимикутамидвогранних кутів між бічними гранями є безпосередньо кути основи.
319
Геометрія
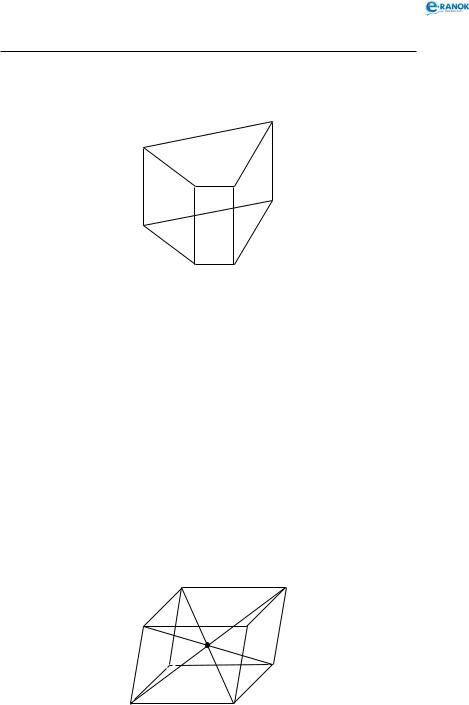
Приклад
На рисунку ABCDA1B1C1D1 — пряма призма .
B1
A1
D1 C1
B
A
DC
DAB — лінійний кут двогранного кута між гранями
AA1D1D і AA1B1B.
Призма називається п р а в и л ьн о ю, якщо:
•в основі її лежить правильний многокутник ;
•призма є прямою.
Паралелепіпед
Паралелепіпедом називається призма, в основі якої лежить паралелограм.
Усі грані паралелепіпеда — паралелограми .
Грані паралелепіпеда, які не мають спільних вершин,
називаються п р о т и л е ж н и м и.
Теорема 1. Протилежні грані паралелепіпеда є паралельними й рівними.
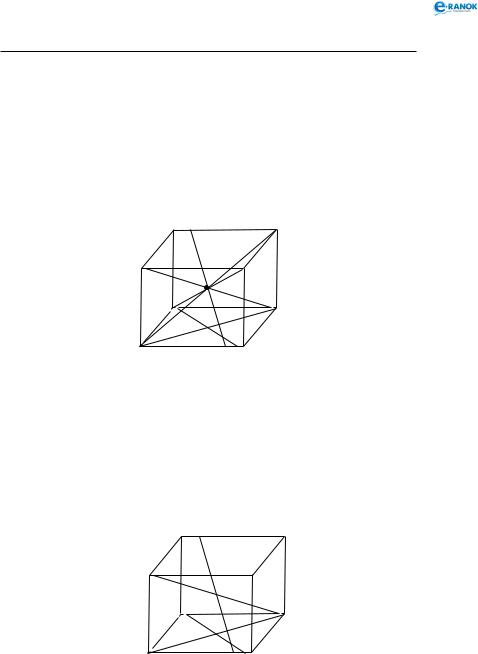
Паралелепіпед залишається паралелепіпедом у всіх випадках, коли за його основу вважаємо довільну його грань (див. рисунок).
Теорема 2. Діагоналі паралелепіпеда перетинаються в одній точці й точкою перетину діляться навпіл.
320
Стереометрія. Многогранники
Із цього випливає, що точка перетину діагоналей паралелепіпеда є його центром симетрії .
Зверніть увагу: у прямого паралелепіпеда є чотири діагоналі, які попарно дорівнюють одна одній.
На рисунку B1D = D1B; A1C = C1 A. |
|
|
Це випливає з |
властивостей |
похилих, оскільки |
AA1 = BB1 = CC1 = DD1 |
— рівні перпендикуляри до площини |
|
основи ABCD. |
|
|
|
B1 |
C1 |
A1 D1
BC
AD
Якщо дві діагоналі прямого паралелепіпеда виходять із сусідніх вершин, то більша з них та, яка проектується у більшу діагональ основи, тобто в таку діагональ паралелограма, яка лежить проти тупого кута. Отже, якщо на наведеному вище рисунку вважати кут ABC тупим, отримаємо
AC > BD, A1C > B1D.
Прямий паралелепіпед, у якого основою є прямокут-
ник, називається п р я м о к у т н и м п а р а л е л е п і п е д о м
(див. рисунок).
d
c
b
a
Усі грані прямокутного паралелепіпеда — прямокутники, які можна розбити на три пари рівних між собою. Довільну грань прямокутного паралелепіпеда можна вважати його основою. Враховуючи, що при паралельному
321
Геометрія
проектуванні довільний паралелограм може зображуватися довільним паралелограмом, зображення прямокутного паралелепіпеда ніяк не відрізняється від зображеня будьякого прямого паралелепіпеда.
Довжини непаралельних ребер називаються л і н і й н и м и р о з м і р а м и (вимірами) прямокутного паралелепіпеда.
Теорема 3. У прямокутному паралелепіпеді всі діагоналі рівні. Квадрат діагоналі дорівнює сумі квадратів трьох його вимірів.
Усі двогранні кути прямокутного паралелепіпеда є прямими.
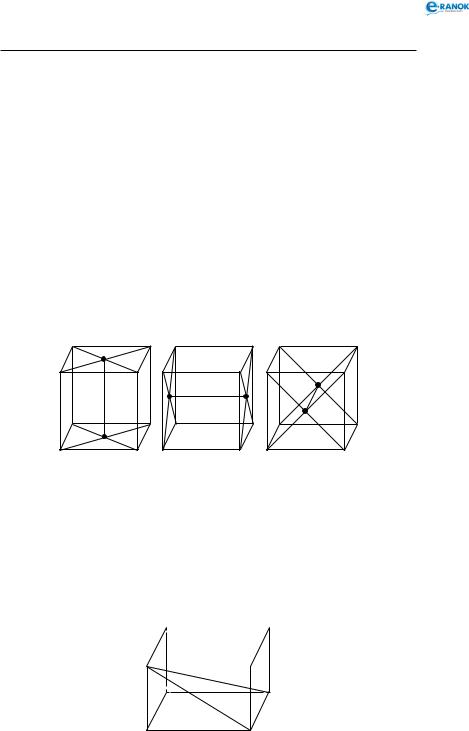
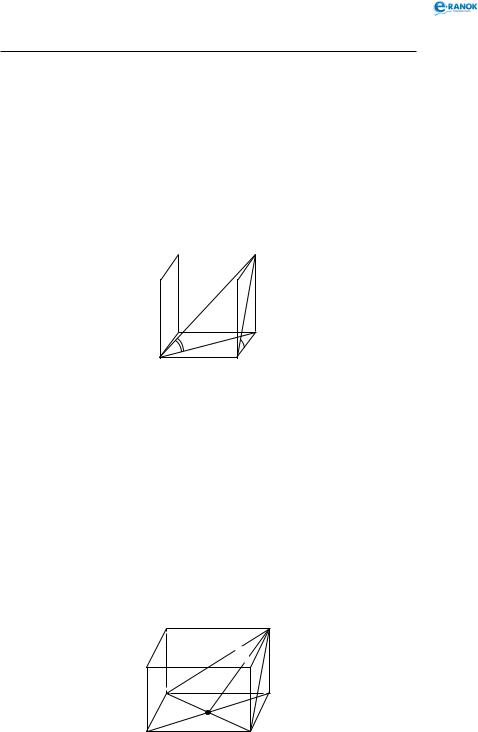
Прямокутний паралелепіпед має три пари рівних між собою діагональних перерізів. Кожний із цих перерізів є прямокутником (див. рисунки ).
Кожна пара перерізів перетинається по прямій, яка проходить через точки перетину діагоналей протилежних граней. Відрізки між цими точками є паралельними й дорівнюють одному з ребер прямокутного паралелепіпеда.
Прямокутним є трикутник, який утворюється діагоналлю прямокутного паралелепіпеда, діагоналлю бічної грані й стороною основи (див. рисунок). Наприклад, A1DC
( A1DC = 90°).
B1 |
|
|
C1 |
|
|
|
|||
A1 |
|
D1 |
||
|
|
|
|
|
B C
AD
322
Стереометрія. Многогранники
Прямокутний паралелепіпед має центр симетрії — це точка перетину його діагоналей. Він також має три площини симетрії, які проходять через центр симетрії паралельно граням.
Прямокутний паралелепіпед, у якого всі ребра рівні, називається к у б о м.
Площина будь-якого діагонального перерізу куба є його площиною симетрії. Таким чином, куб має дев’ять площин симетрії. На рисунку розглянемо взаємне розміщення деяких елементів прямого паралелепіпеда:
B1 |
|
|
C |
|
|
|
|||
|
|
1 |
||
A1 |
|
D1 |
||
|
|
|
|
|
BC
AD
C1DC — кут між діагоналлю бічної грані й площиною основи (C1C — перпендикуляр, C1D — похила, СD — проекція).
C1 AC — кут між діагоналлю прямого паралелепіпеда й площиною основи (C1C — перпендикуляр, AC1 — похила, АС — проекція).
AC1D — кут нахилу діагоналі AC1 до бічної грані DD1C1C (AD — перпендикуляр, AC1 — похила, DC1 — проекція).
Нехай ABCDA1B1C1D1 — прямий паралелепіпед (див. рисунок), де ABCD — ромб. Проведемо його переріз площиною, що проходить через діагональ основи BD і вершину C1.
B1 |
C1 |
A1 |
D1 |
|
|
B |
C |
|
|
|
O |
A |
D |
323
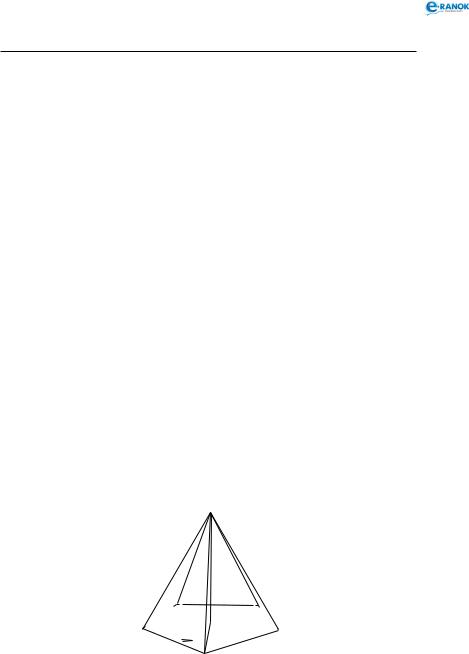
Геометрія
У перерізі отримаємо рівнобедрений трикутник BC1D.C1OC — лінійний кут двогранного кута між площинами основи й перерізу. CO BD за властивістю діагоналей ромба, C1C — перпендикуляр, C1O — похила, СО — проекція. За теоремою про три перпендикуляри: C1O BD.
Піраміда |
|
П і р а м і д о ю називається многогранник, |
який скла- |
дається з плоского многокутника — о с н о в и |
п і р а м і д и, |
точки, яка не лежить у площині основи — в е р ш и н и п і р а м і д и і всіх відрізків, що сполучають вершину піраміди з точками основи. Відрізки, що сполучають вершину піраміди з вершинами основи, називаються б і ч н и м и р е
бр а м и.
Ви с о т а п і р а м і д и — перпендикуляр, опущений із вершини піраміди на площину основи.
Піраміда називається n-к у т н о ю, якщо її основою є n-кутник. Трикутна піраміда називається також т е т р а е д р о м. Б і ч н а г р а н ь п і р а м і д и — трикутник. Однією з його вершин є вершина піраміди, а протилежною стороною — сторона основи піраміди.
На рисунку SO — висота піраміди. Тоді OAS — кут між бічним ребром і площиною основи (SO — перпендикуляр, SА — похила, OА — проекція).
S
BC
A  O
O  D
D
F
E
З основи висоти піраміди (точки О) проведемо перпендикуляр на сторону основи (наприклад АЕ). Основу цього перпендикуляра (точку F) з’єднаємо з вершиною піраміди (точкою S). За теоремою про три перпендикуляри SF AE. (SO — пер-
324
Стереометрія. Многогранники
пендикуляр, SP — похила, OF — проекція, OF AE за побудовою.) Отже, SFO — лінійний кут двогранного кута між площиною бічної грані ASE і площиною основи.
Для розв’язування задач про піраміду дуже важливо з’ясовувати, де розміщена основа її висоти.
1.Якщо виконується хоча б одна з таких умов:
•усі бічні ребра піраміди рівні,
•усі бічні ребра нахилені до площини основи під одним і тим самим кутом,
•усі бічні ребра утворюють однакові кути з висотою піраміди,
•усі бічні ребра рівновіддалені від основи висоти, — то основою висоти піраміди є центр кола, описаного навколо основи піраміди.
Бічне ребро l, висота H і радіус R описаного навколо
основи кола утворюють прямокутний трикутник:
l
H
O
R
У цьому випадку бічну поверхню можна знайти за фор-
мулою S1 = 1 l2 (sinα+…+sinαn ), де l — довжина бічного ребра, α1,...,2 αn — плоскі кути при вершині.
2.Якщо виконується хоча б одна з таких умов:
•всі бічні грані нахилені до площини основи під одним і тим самим кутом,
•усі бічні грані мають однакові висоти,
•висоти бічних граней утворюють однакові кути з висотою піраміди,
•бічні грані рівновіддалені від основи висоти, — то основа висоти лежить у центрі кола, вписаного в основу піраміди.
На рисунку OSP — прямокутний ( |
SOP = 90° |
), |
OP = r — радіус вписаного кола в ABCDEF; |
|
|
|
|
325
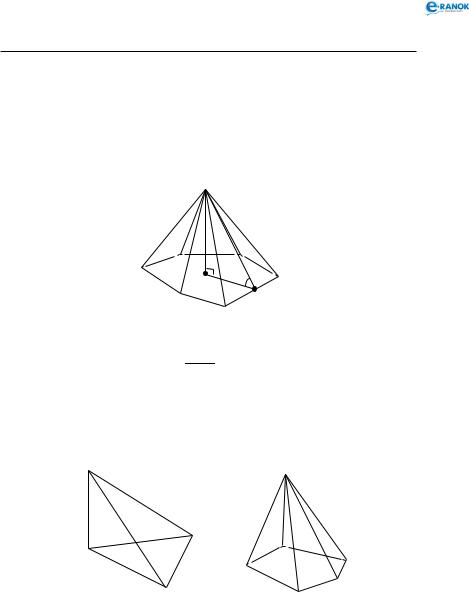
Геометрія
H = SO — висота піраміди, SP — висота бічної грані;
ϕ— лінійний кут двогранного кута між бічною гранню
йплощиною основи;
О— центр вписаного в основу кола, тобто точка перетину бісектрис ABCDEF.
|
S |
|
|
B |
H |
|
C |
A |
O |
ϕ |
D |
|
r |
||
F |
|
P |
|
|
|
E |
|
У цьому випадку 4¾ 4ËÎÊ .
DPTϑ
3.Якщо бічне ребро перпендикулярне до площини основи, то це ребро є висотою піраміди (див. рисунки).
S S
|
A |
B |
|
A |
|
|
|
||
|
|
|
B |
|
|
|
|
C |
|
|
|
|
|
|
|
C |
|
|
K |
|
|
|
D |
У цьому випадку SBA і SCA — кути нахилу бічних ребер SВ і SС відповідно до площини основи. BAC є лінійним кутом двогранного кута між бічними гранями SAC
іSBA.
4.Якщо бічна грань перпендикулярна до площини основи (див. рисунок нижче), то висотою піраміди буде висота цієї грані (за теоремою «Якщо пряма, яка лежить в одній
326
Стереометрія. Многогранники
із двох перпендикулярних площин, перпендикулярнадо прямої їх перетину, то вона перпендикулярна до другої площини »).
S
H
A  B
B
O
C
D
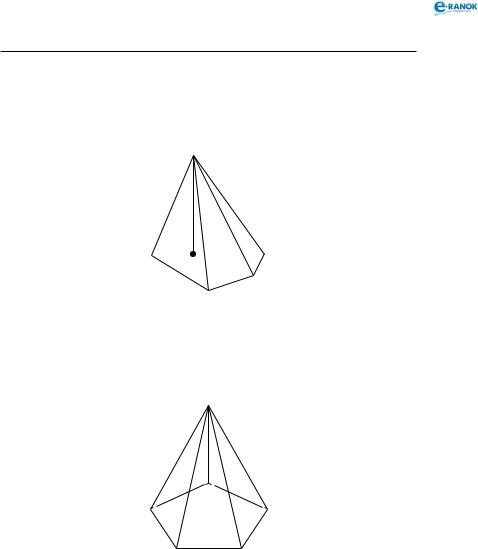
5.Якщо дві бічні грані перпендикулярні до площини основи, то висотою піраміди є їх загальне бічне ребро:
S
H
A
BC
FD
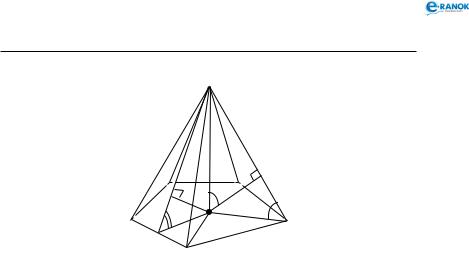
Відстані від основи висоти піраміди
Відстань від основи висоти піраміди до бічного ребра — перпендикуляр, опущений із точки О на це ребро (див. рисунок). Зверніть увагу (OF SE, але OFS на рисунку не повинен бути прямим кути при паралельному проектуванні не зберігаються).
OF — відстань від основи висоти до бічного ребра SE. OF = Hcosα , де α — кут між ребром SE і площиною
основи.
327
Геометрія
S
|
C |
H |
D |
F |
|
α |
|
|
|
|
N |
|
α |
|
|
|
|
||
B |
ϕ |
O |
|
|
|
E |
|||
|
K |
|
|
|
|
A |
|
|
|
Нехай OK AB, тоді |
SK AB |
за |
теоремою про |
три перпендикуляри. Отже, AB перпендикулярна до пло- |
|||
щини SOK. Звідси, якщо |
ON SK , |
то |
ON перпенди- |
кулярна до площини ASB. |
|
|
|
ON — відстань від основи висоти до бічної грані ASB.
ON = Hcosϕ.
Правильна піраміда
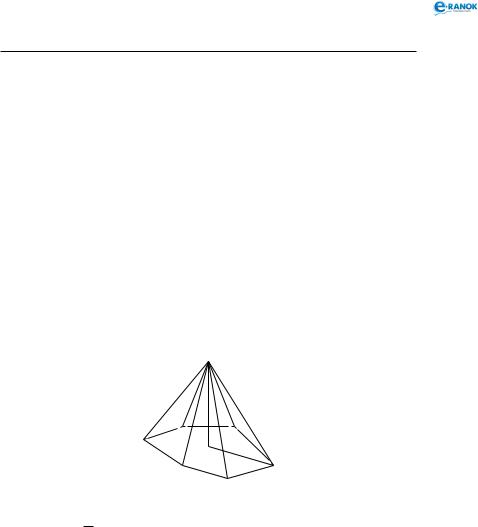
Піраміда називається п р а в и л ьн о ю, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника. В і с с ю правильної піраміди називається пряма, яка містить її висоту. Бічні ребра правильної піраміди рівні, бічні грані — рівні рівнобедрені трикутники. Висота бічної грані, проведена з вершини піраміди, називається а п о ф е м о ю. Вона є бісектрисою та медіаною бічної грані, оскільки та є рівнобедреним трикутником.
Теорема. Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.
4¾ |
1M |
; |
4 |
B O M |
, |
|
|||||
|
|
||||
|
|
¾ |
|
|
|
|
|
|
|||
де Р — периметр основи, а — сторона основи, l — довжина апофеми.
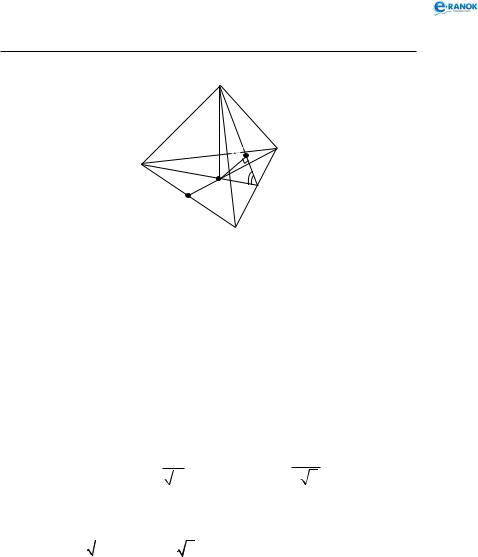
Правильна трикутна піраміда
В основі правильної трикутної піраміди лежить рівносторонній трикутник, який зображується довільним трикутником (див. рисунок).
328
Стереометрія. Многогранники
S
N α B A
B A
ϕ
O  D
D
C
Центром ABC є точка перетину його бісектрис, котрі водночас є висотами і медіанами. Медіани при паралельному проектуванні зображуються медіанами. Тому будуємо дві медіани основи. Точка їх перетину — основа висоти піраміди. Зображуємо висоту, а потім з’єднуємо вершину піраміди з вершинами основи. Отримаємо бічні ребра.
Нарисунку: SBO = α —кутнахилубічногоребрадопло- щиниоснови(однаковийдлявсіхребер); SDO = ϕ —кутнахи- лубічноїгранідоплощиниоснови(однаковийдлявсіхграней).
Нехай AB = BC = AC = a. |
|
|
|
Тоді |
OB = R = a ; |
OD = r = a ; |
R =2r; |
32 3
SO = H; H = Rtgα; H = rtgϕ.
Отже, tgϕ =2tgα.
4 |
B |
|
|
; |
4 |
B |
|
|
. |
|
|
|
|
|
|
||||
ËÎÊ |
|
|
|
|
¾ |
DPTϑ |
|||
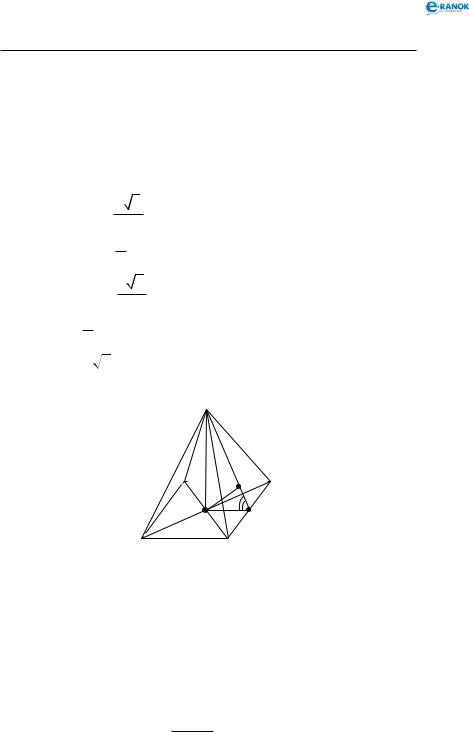
Площина осьового перерізу ASD є площиною симетрії правильної трикутної піраміди.
Ця площина перпендикулярна до площини основи і площини грані BSC.
Цікаво також відмітити, що мимобіжні ребра піраміди (SA і BC, SB і AC, SC і AB) є перпендикулярними. Якщо ON SD, то ON є відстанню від основи висоти не тільки до апофеми, а й до бічної грані BSC.
ON = rsinϕ.
329
Геометрія
Правильна чотирикутна піраміда
В основі правильної чотирикутної піраміди лежить квадрат , який зображується довільним паралелограмом. Його центром є точка перетину діагоналей. Ця точка — основа висоти піраміди.
Нехай сторона квадрата а (див. рисунок).
Тоді OC = R = a 2 ;
2
OM = r = a ;
2
H = SO = a 2 tgα;
2
H = a tgϕ;
2
tgϕ = 2 tgα.
S
B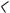 Nα
Nα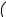 C
C
|
ϕ |
O |
M |
|
AD
Зверніть увагу: OM = r , OM CD, тобто OM BC. При паралельному проектуванні паралельність зберіга-
ється.
4 |
B ; 4 |
B |
. |
|
|||
ËÎÊ |
¾ |
DPTϑ |
|
Відстань від основи висоти до бічної грані:
ON = r sinϕ; ON = a sinϕ .
2
330
Стереометрія. Многогранники
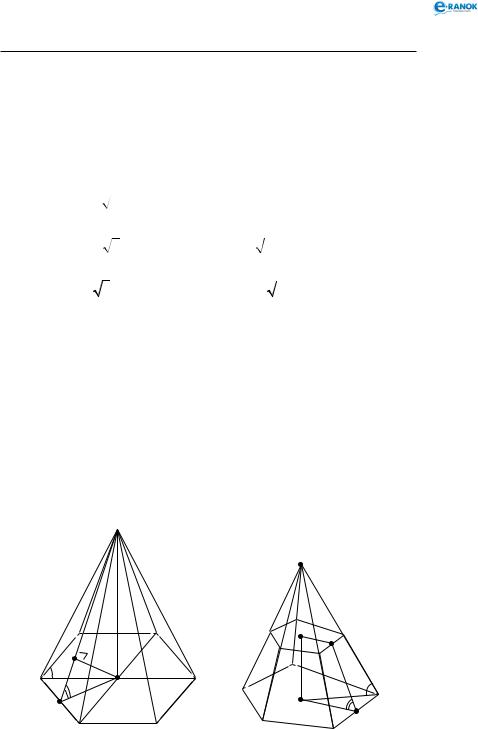
Правильна шестикутна піраміда
В основі правильної шестикутної піраміди лежить правильний шестикутник (див. рисунок нижче ліворуч). Його центром є точка перетину діагоналей. Ця точка — основа висоти піраміди.
Тоді OD = R = a;
Нехай сторона правильного шестикутника а.
OM = r = |
|
a 3 |
; |
H = SO = atgα; |
|||||||||||
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
H = SO = |
a 3 |
tgϕ; |
tgα = |
3 |
|
tgϕ. |
|||||||||
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
||||||||||
4 |
B |
|
|
; |
4 |
B |
|
|
. |
||||||
|
|
|
|
|
|
|
|
||||||||
ËÎÊ |
|
|
|
|
|
|
¾ |
DPTϑ |
|||||||
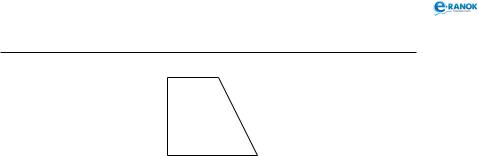
Зрізана піраміда
З р і з а н о ю п і р а м і д о ю називається многоранник, який залишиться, якщо від піраміди відділити площиною, яка паралельна основі, піраміду з тією ж вершиною.
Теорема. Площина, яка паралельна основі піраміди й перетинає її, відтинає подібну піраміду.
Зверніть увагу: щоб правильно зобразити зрізану піраміду, треба починати із зображення вихідної повної піраміди (див. рисунок праворуч).
|
|
S |
|
|
|
|
|
|
|
|
S |
|
|
|
B |
C |
B1 |
C1 |
|
|
|
O1 |
D1 |
|
|||
|
|
|
||||
|
N |
|
A1 C |
E |
F1 |
|
A |
α ϕ |
|
D |
1 |
|
|
O |
|
α |
D |
|||
|
|
B |
|
ϕ |
||
|
M |
|
O |
|
||
|
|
F |
|
|||
|
|
|
|
|
|
|
F E A E
331

Геометрія
Основи зрізаної піраміди — подібні многокутники. Бічні грані — трапеції. OO1 — висота зрізаної піраміди, FF1 — висота бічної грані, D1DO = α — кут нахилу бічного ребра до площини основи (будь-якої), FFO1 = ϕ — кут нахилу бічної грані до площини нижньої основи.
П р а в и л ьн а з р і з а н а п і р а м і д а — це зрізана пі-
раміда, яку дістали з правильної піраміди.
Її бічні ребра рівні й нахилені до площини основи під одним і тим самим кутом. Її бічні грані — рівні рівнобічні трапеції і нахилені до площини нижньої основи під одним і тим самим кутом. Висоти бічних граней піраміди назива-
ються а п о ф е м а м и.
Бічна поверхня правильної зрізаної піраміди дорівнює добутку півсуми периметрів основ і апофеми.
4¾ 1Ê 1¿ M, де Pн і Pв — периметри відповідних
основ, l — апофема.
На рисунках зображені фігури, які доцільно розглянути при розв’язуванні задач на зрізану піраміду .
O SF OSF; |
O S |
= |
|
FS |
= |
|
|
O F |
= |
b |
|
. |
|
||||||||||||
1 |
|
1 |
|
|
|
|
1 1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
1 |
|
|
OS |
|
|
FS |
|
|
|
|
OF |
|
|
|
a |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
E SD ESD; |
SD1 |
= |
SE1 |
= |
E1D1 |
|
= |
b |
. |
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
1 |
1 |
|
|
SD |
|
|
SE |
|
|
|
|
ED |
|
|
|
|
|
a |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
S |
|
F1 |
|
|
E1 |
S |
|
|
|
|
|
|
|
|
|
D1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
O1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
F1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ϕ |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
O |
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
O FFO — прямокутна трапеція. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O1O — висота зрізаної піраміди.
F1F — висота бічної грані.
332
Стереометрія. Многогранники
O1 F1
OF
Увипадку, коли зрізана піраміда правильна, відрізки
OD і O1D1 є радіусами описаного кола, а OF і O1F1 — радіусами вписаного кола для нижньої і верхньої основи відповідно.
Правильні многогранники
Опуклий многогранник називається п р а в и л ьн и м, якщо його грані є правильними многокутниками з однією й тією самою кількістю сторін, а в кожній вершині многогранника збігається одне й те ж саме число ребер.
Існує п’ять типів правильних опуклих многогранників: правильний тетраедр, куб, октаедр, додекаедр, ікосаедр.
1.У правильного тетраедра грані — правильні трикутники; у кожній вершині збігається по три ребра. Тетраедр — трикутна піраміда, усі ребра якої рівні між собою.
2.У куба всі грані — квадрати; у кожній вершині збігається по три ребра. Куб — прямокутний паралелепіпед із рівними між собою ребрами.
3.В октаедра грані — правильні трикутники. У кожній його вершині збігається по чотири ребра.
4.У додекаедра грані — правильні п’ятикутники. У кожній його вершині збігається по три ребра.
5.В ікосаедра грані — правильні трикутники. У кожній його вершині збігається по п’ять ребер.
На рисунках наведено приклади правильних много-
гранників із назвами.
333
