Лекція 16. Тертя в поступальних кінематичних парах

План лекції :

16.1. Види тертя. Тертя ковзання сухих тіл.

16.2. Тертя на похилій площині.

16.3. Тертя в клинчастому І циліндричному жолобі. 16. 4. Тертя, в гвинтовій парі.

16. 1. Види тертя. Тертя ковзання сухих тіл.

При вирішенні багатьох питань, які відносяться до динаміки ме­ханізмів і машин, поряд з рушійними силами і силами виробничих опо­рів приходиться враховувати також і сили тертя.

Загальний опір, що виникає в місцях дотику двох тіл, які пере­міщаються одне відносно одного, називається силою тертя. Тертя - це складне явище, для пояснення якого створені дві гіпотези: механічна і молекулярна.

За сучасною гіпотезою, що має змішанний характер, процес тертя при ковзанні поверхонь є результатом не лише механічної взаємодії поверхонь, але і результатом дії молекулярних сил.

Ми не будемо зупинятися на сучасних теоріях, які пояснюють при­роду тертя, а зупинимося тільки на викладенні елементарних відомос­тей з теорії тертя, необхідних для вирішення простих задач теорії механізмів. В загальному тертя розрізняють таких видів:

а/ чисте - сухе;

б/ граничне, якщо поверхні розділяє шар мастила завтовшки не більше ніж 0,1 Мкм;

в/ рідинне, поверхні певністю розділені шаром мастила;

г/ напівсухе - одночасно сухе і граничне;

д/ напіврідинне - одночасно рідинне і граничне.

По видам рухів розрізняють:

а/ тертя ковзання;

б/ тертя кочення.

Сила F_f сухого тертя, яка виникає при відносному ковзанні од­ного тіла відносно іншого, пропорційна силі F_N нормального тиску і визначається із рівняння Амонтона-Кулона

F_f = f F_N,

де f - коефіцієнт тертя ковзання.

Коефіцієнт тертя f залежить від матеріалів поверхонь що труть­ся, їх стану та обробки, мащення та інших факторів.

Не дивлячись на це, коефіцієнт тертя f для конкретних матеріалів приймається сталим.

Сила тертя завжди напрямлена в сторону, протилежну швидкості відносного ковзання тіла.

П овна реакція F_R ланки 2 на ланку 1 визначається додаванням нормальної реакції F_N і сили тертя F_f /рис.16.1/.

Визначення кута тертя

Рис.16.1

Повна реакція F_R відхилена від нормальної реакції F_N на кут φ, який називається кутом тертя ковзання

/16.2/

Таким чином, коефіцієнт тертя дорівнює тангенсу кута тертя.

16.2. Тертя на похилій площині.

Знайдемо рушійну силу F_Р, необхідну для рівномірного перемі­щення тіла 1, на яке діє гравітаційна сила F_g /сила тяжіння/, вгору на похилій площині 2, якщо коефіцієнт тертя ковзання рівний f . Похила площина і рушійна сила F_Р складають з горизонталлю кути, відповідно α і β /рис.16.2,а/.

При рівномірному переміщенні тіла 1 на похилій площині 2 вгору на нього діють: рушійна сила F_Р, сила тяжіння F_g, нормальна реакція F_N та сила тертя F_f .

Знайдемо повну реакцію F_R шляхом додавання нормальної реакції F_N та сили тертя F_f . Реакція F_R складає з нормаллю до площини кут тертя φ.

Складемо векторне рівняння всіх сил, що діють на тіло 1:

/16.3/

Тіло на похилій площині

а - переміщення тіла вгору; б - план сил

Рис. 16. 2

Побудуємо план сил /рис. 16. 2, б/. Отримаємо замкнутий силовий трикутник із відповідними кутами при вершинах. На основі теореми синусів можна записати:

/16.4/

Звідси знайдемо рушійну силу

/16.5/

Якщо сила F_Р горизонтальна, кут β=0, то рівняння /16.5/ прийме вигляд:

/16.6/

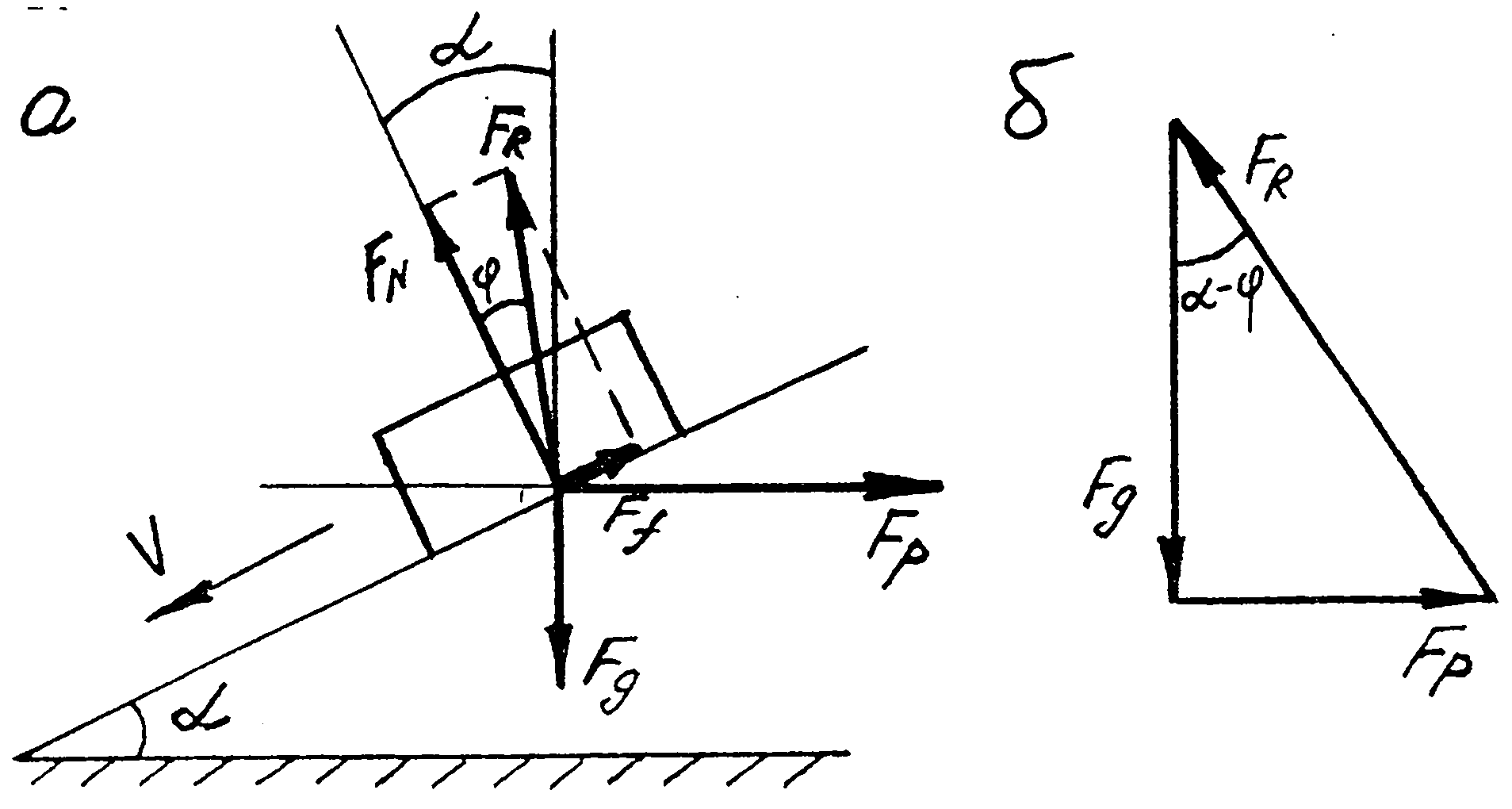
Розглянемо випадок, коли тіло 1 рухається рівномірно донизу /рис.16.З,а/.

В цьому разі побудова відрізняється від попередньої тим, що сила тертя F_f напрямлена вверх, а повна реакція F_R відхиляється на кут тертя φ, не ліворуч від нормалі /рис. 16. 2, а/, а праворуч від неї /рис.16.3,а/.

Для цього випадку досить у формулах /16.5/ і /16.6/ замінити кут φ на –φ. Тоді будемо мати:

/16.7/

/16.8/

Тіло на похилій площині

а - переміщення тіла донизу; б - план сил

Рис. 16. З

Рівняння /16.8/ також випливає із /рис. 16. З, б/.

При відсутності тертя /кут φ = 0/ рівняння /16.8/ набере вигляду:

/16.9/