Лекція24.

Зрівноваження і віброзахист механізмів і машин

План лекції:

24.1. Загальні положення.

24.2. Зрівноважування обертових тіл.

24.3. Зрівноважування механізмів.

24.4. Статичне і динамічне балансування обертових тіл.

24.5. Віброзахист машин.

24.1. Загальні положення.

В кінці XIX століття широкого застосування набули швидкохідні ма­шини, в зв'язку з чим і постала задача зрівноважування і віброзахисту механізмів і машин.

Під час руху ланок механізму у кінематичних парах виникають, крім статичних зусиль, додаткові зусилля - так звані динамічні тиски, які передаються на станину і фундамент механізму. Ці змінні за величиною і напрямом динамічні тиски спричиняють коливання і вібрації опор та фундаменту механізмів і особливо небезпечні бувають у тих випадках, коли частота вібрацій збігається з частотою власних коливань станини, тобто при наявності резонансу. Крім того, динамічні зусилля, які ви­никають під час руху механізму, збільшують сили тертя в опорах валів, спрацювання підшипників і створюють в ланках механізму додаткові нап­руження.

У сучасній техніці зрівноважування механізмів має дуже важливе значення, оскільки багато механізмів і машин працюють на великих швидкостях. А тому в процесі проектування механізму ставиться задача зрівноважування механізмів, тобто повного або часткового погашення динамічних зусиль.

Досліджуючи питання про зрівноважування механізму на його фунда­менті , вивчатимемо дві задачі :

1/ зрівноважування окремих обертових ланок;

2/ зрівноважування механізму в цілому.

Динамічні зусилля на фундамент від машини виникають тоді, коли система сил інерції не дорівнює нулю, А тому задача про зрівноважу­вання мас заключається в такому розподілі їх в машині , при якому си­ли інерції і моменти пар сил інерції були б рівні нулю, або достатньо малі. Позначимо головний вектор сил інерції і головний момент пар сил інерції .

Тоді вимога, щоб динамічні зусилля на фундамент були відсутніми, зводиться до системи рівнянь:

= 0 і = 0 ,

або в проекціях на осі координат:

/24.1/

24.2. Зрівноважування обертових тіл.

Незрівноваженість тіл обертання, яка викликана недосконалістю технологічного процесу їх виготовлення, усувається шляхом прибавлення або видалення невеликої маси матеріалу. Виправлення такої незрівноваженості називається балансуванням.

Незрівноваженість, яка виникає внаслідок конфігурації деталі /колінвал, кулачок/ усувається шляхом встановлення противаг.

Нехай потрібно зрівноважити три маси, що обертаються на валу і центри мас яких розміщені в одній площині /рис. 24.1, а/. В цьому ви­падку достатньо підібрати четверту масу так, щоб центр її мас також знаходився в цій же площині, а радіус-вектор загального центру мас дорівнює нулю r_S = 0.

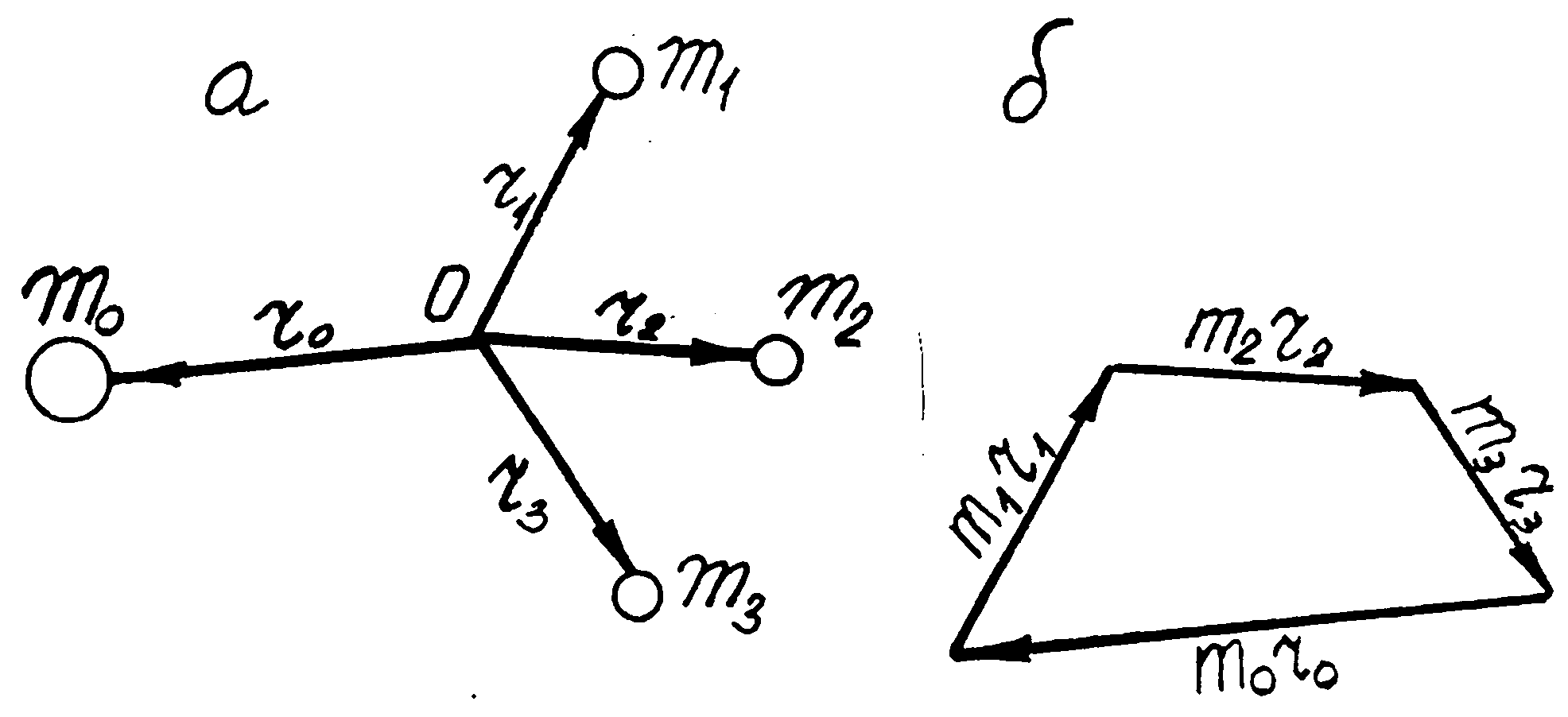Зрівноваження противагою

Рис. 24.1.

Відстані центрів мас т₁, т₂, т₃ і т₀ до осі обертання позначимо r₁, r₂, r₃ i r₀

Відцентрові сили інерції кожної маси дорівнюють:

/24.2/

Для зрівноваження необхідно, щоб головний вектор сил інерції до­рівнював нулю = 0, тобто

/24.3/

або враховуючи /24.2/

Це і є умова статичного зрівноважування обертових тіл.

Задача вирішується графічним складанням векторів т_іr_i. /рис.24.1,б/,

При цьому вектор m_or_o показує напрям радіуса-вектора, на якому пот­рібно встановити противагу, задаючись величиною радіуса r_o, знайдемо масу противаги r_o.

Якщо площину кріплення противаги конструктивно не можливо вибрати в тій же площині обертання що і незрівноважені маси, то встановлюють дві противаги в двох перпендикулярних, до осі обертання, площинах /рис.24.2/.

При цьому необхідно виключити можливість виникнення додаткових зусиль на підшипники не тільки від результуючої сили інерції, а і від моментів пар сил інерції.

Складемо рівняння моментів

/24.5/

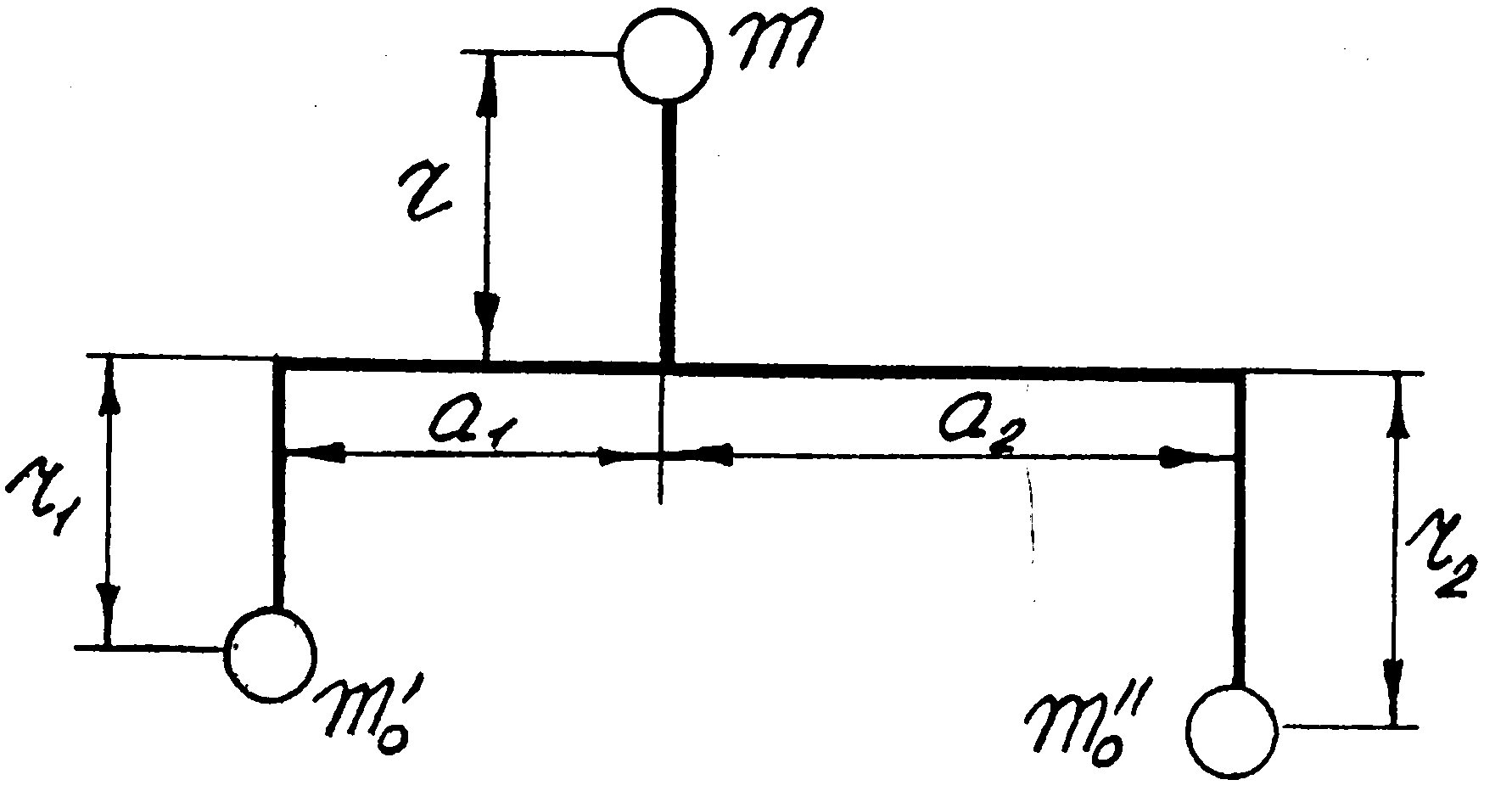Зрівноважування двома противагами

Рис.24.2.

Встановленням двох противаг масами m_o` i m<sub>o</sub>`` досягається повне зрівноважування маси m, при цьому необхідно, щоб центри мас m, m<sub>o</sub>` i m_o`` знаходилися в одній площині, яка проходить через вісь обертання.

Розглянемо задачу про зрівноважування вала, на якому жорстко зак­ріплені маси m₁, m₂ i m₃ розміщені в трьох площинах, які перпенди­кулярні до осі обертання /рис.24.З,а/.

Зрівноваження мас в різних площинах

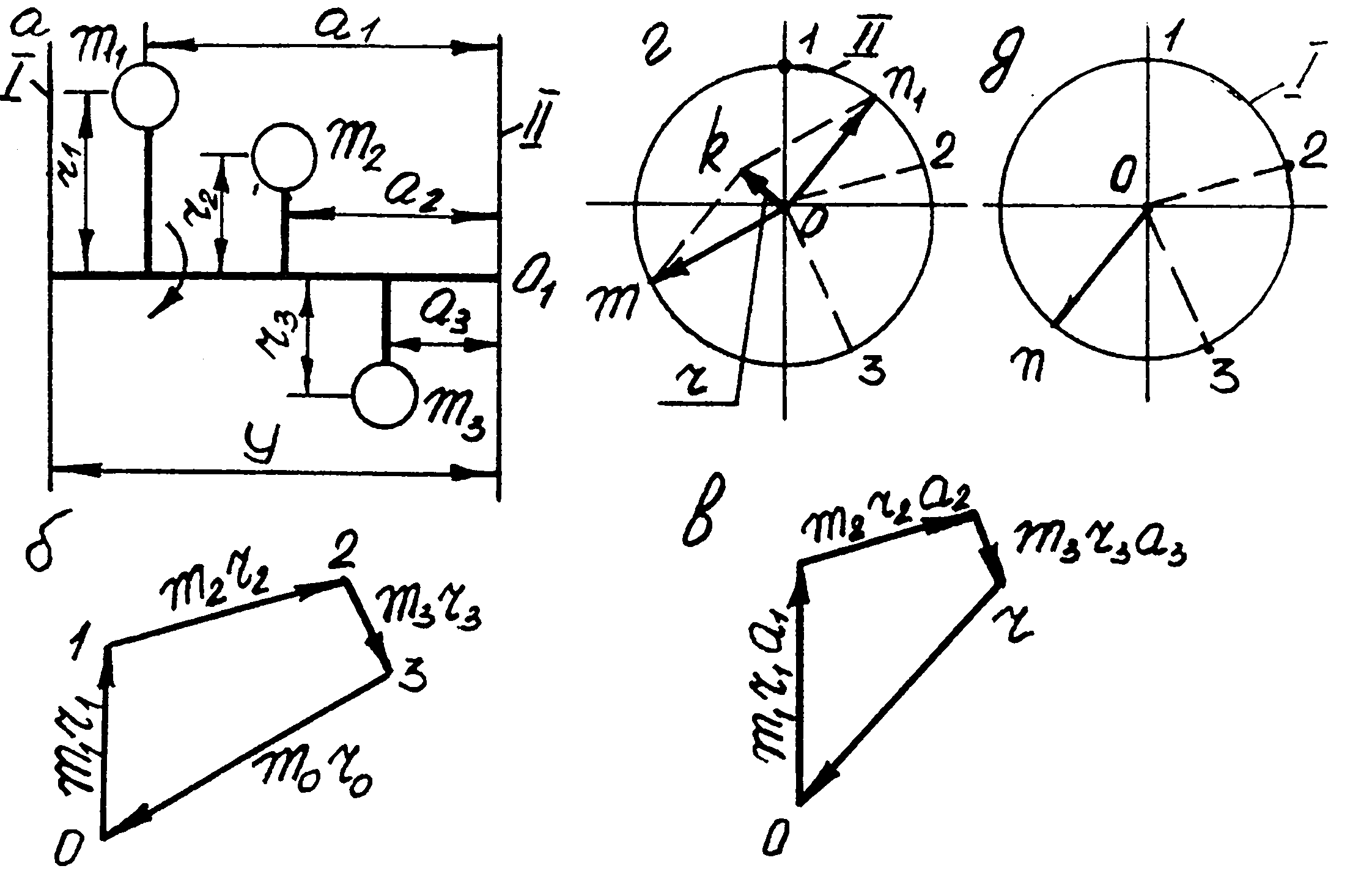Рис.24.3.

Умова відсутності тиску на підшипники від головного вектора сил інерції F_і i головного моменту пар сил інерції відносно центра зведення О₁ виражається рівняннями:

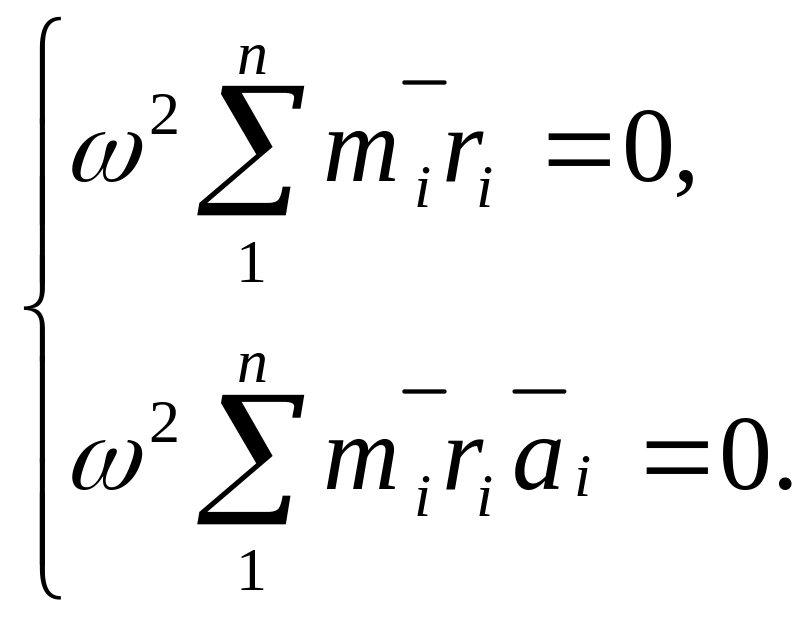/24.6/

Будуємо многокутники векторів сил /рис.24.З,б/ і векторів моментів /рис.24.З,в/. Зрівноважувальним у першому випадку є вектор , зоб­ражений на площині 2 вектором от /рис.24.3,г/, а в другому - век­тор , який зображає повернутий момент пари векторів , що ле­жить у площині 1 /рис.24.3,д/ і , що лежить у площині 2. Величи­на кожного з них дорівнює r₀/y.

Таким чином, задані маси m₁, m₂ і m₃ будуть цілком зрівноважені двома масами, розміщеними вздовж у площині 1 і вздовж рівнодійної ОK y площині 2.

З викладеного випливає: будь-яка кількість мас, що лежить у різ­них площинах обертання, зрівноважується двома противагами, які вста­новлюються в двох довільних площинах, перпендикулярних до осі обер­тання при додержанні двох умов рівноваги векторів:

i

тобто і /24.7/