З убчасті механізми з рухомими осями

а – планетарний механізм Джемса; б – диференціальний механізм

Рис. 13.2

Будь яку диференціальну передачу можна перетворити в планетарну шляхом закріплення одного із коліс.

Зубчасте колесо 1 обертається навколо осі і знаходиться в зачепленні разом з колесом 2. Колесо 2 знаходиться одночасно в двох рухах :в обертанні разом з водилом Н і з кутовою швидкістю ω_H навколо нерухомої спільної осі 0-0 механізму, залишаючись у той самий час у постійному зачепленні з колесами 1 та 3 і в обертанні з кутовою швидкістю ω₂^H навколо своєї власної осі. Зубчасте колесо 3 обертається в диференціальному механізмі і воно нерухоме /опорне/ в планетарному механізмі.

На рис 13.3 показано складний зубчастий механізм з рухомими осями з зовнішнім зачепленням /рис. 13.3, а/ і внутрішнім зачепленням /13.3, б/. Якщо всі колеса механізму обертаються, то ступінь вільності – два і це буде диференціальний механізм, якщо одне із коліс закріпити – перше чи третє, то ступінь вільності буде одиниця і тоді це буде планетарний механізм, який має назву редуктора Давида.

Зубчасті механізми типу редуктора Давида

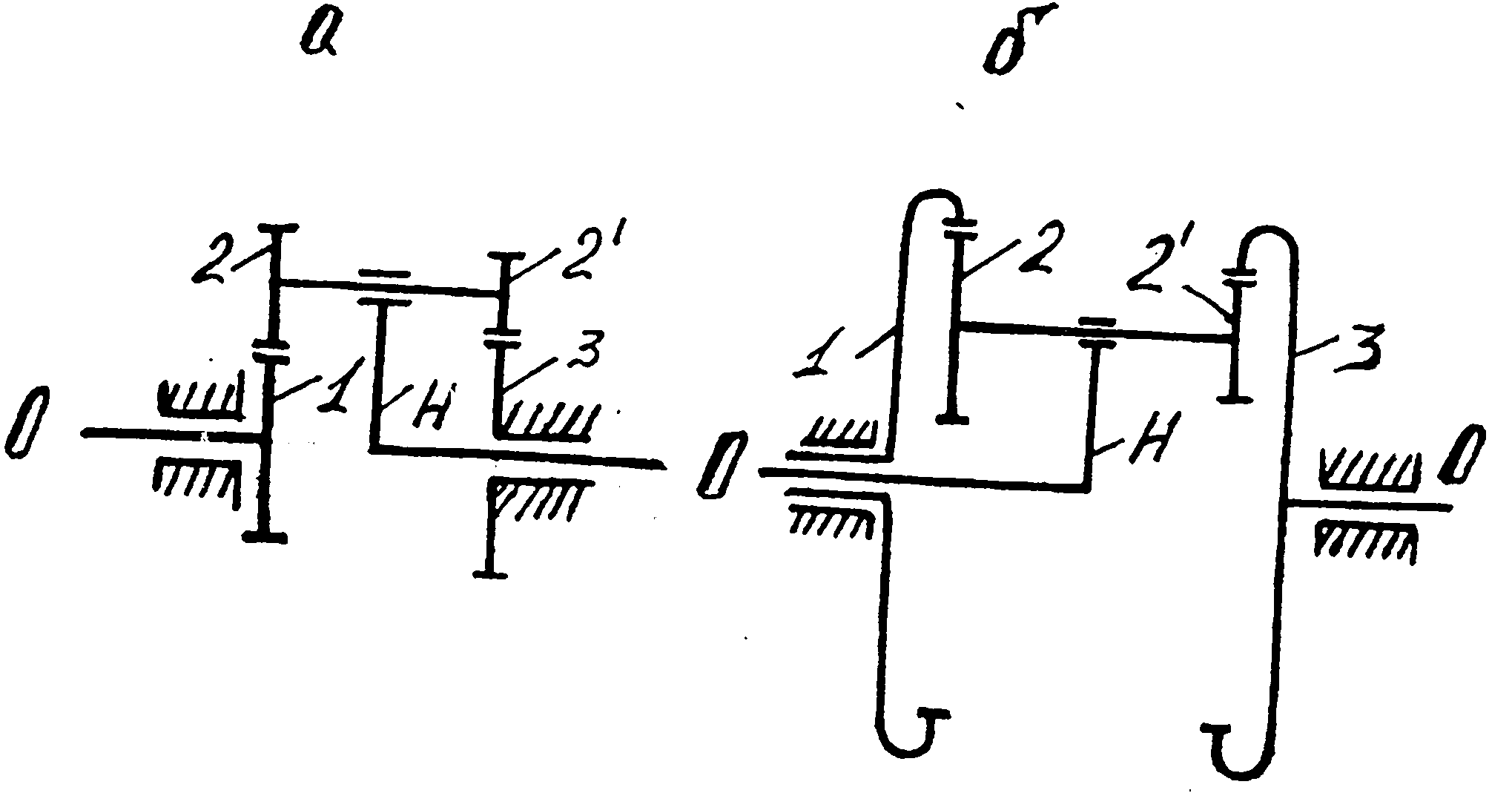а – з зовнішнім зачепленням; б – з внутрішнім зачепленням.

Рис. 13.3

Планетарний механізм Диференціальний механізм

	n	P5	P4
	1	O-1	1-22'
	2-2'	22'-H	22'-3
	H	H-O	-
Σ	3	3	2

	n	P5	P4
	1	1-0	1-22'
	22'	22'-Н	22'-3
	3	3-О	-
	Н	Н-1	-
	4	4	2

W=3*3-2*3-2=1. W=3*4-2*4-2=2.

13. 3 Кінематика диференціальних та планетарних механізмів

Для виведення формули, що зв'язує швидкості ланок диференціального механізму, застосовуємо метод Вілліса, що ґрунтується на принципі обертання руху.

Надамо усім ланкам механізму додаткового обертання навколо осі 0-0 з кутовою швидкістю – ω_н, що дорівнює за величиною, але протилежна за знаком кутовій швидкості водила Н. Застосувавши метод обертання руху, умовно перетворимо диференціальний механізм в обернений тобто у звичайний зубчастий механізм з нерухомими осями.

Від кутової швидкості кожної ланки віднімемо кутову швидкість ω_н водила.

Для редуктора Джемса /рис.13.2, б/ маємо :

Номер ланки	Кутова швидкість дифер. механізму	Кутова швидкість обернен. механізму
1 2 3 Н	ω1 ω2 ω3 ωн	ω1 - ωн ω2 - ωн ω3 – ωн ωн -ωн=0

Передаточне відношення від ланки 1 до ланки 3 в оберненому механізмі

. /13.5/

Формула /13.5/ зв'язує між собою швидкості обертання центральних коліс 1 і 3 і водила Н. Задавшись двома із них завжди можна найти третю швидкість. Для цього потрібно знати числа зубів коліс. Тоді передаточне число, як для механізму з нерухомими осями, знайдемо аналогічно /13.3/ і /13.4/

. /13.6/

Знак «-» - показує, що зубчасті колеса обертаються в різні сторони /зовнішнє зачеплення/, а «+» - в одну сторону /внутрішнє зачеплення/.

Для редуктора Давида /рис. 13.3, а/

/13.7/

Передаточне число планетарного механізму отримаємо, застосувавши також метод обертання руху.

Номер ланки	Кутова швидкість планетар. мех – му	Кутова швидкість оберненого мех – му.
1	2	3
1 2 3 Н	ω1 ω2 ω3=0 ωH	ω2-ωH -ωH ωH-ωH=0

Передаточне відношення від ланки 1 до ланки 3 в оберненому механізмі:

/13.8/

Оскільки _, то рівняння /13.8/ запишемо так

. /13.9/

Передаточне відношення планетарної передачі дорівнює одиниці мінус передаточне відношення оберненого механізму.

Враховуючи /13.6/ для редуктора Джемса

. /13.10/

Враховуючи /13.7/ для редуктора Давида

. /13.11/

Приклад: Визначити передаточне відношення U^н₁₄ для редуктора Давида

/рис. 13.3/, а/ при z₁=z¹₂ =100, z₂=99, z₃=101.

Згідно /13.11/ маємо:

.

Центральне колесо 1 буде обертатися в 10000 раз повільніше водила Н.