24.3. Зрівноважування механізмів.
Для зовнішнього зрівноважування плоского механізму необхідно і достатньо так підібрати маси цього механізму, щоб:
а/ спільний центр мас усіх його рухомих ланок залишався нерухомим
xS = const; yS = const; /24.8/
б/ динамічні моменти інерції мас усіх ланок механізму відносно площин Zx і yZ були сталі
Ixz = const; Iyz = const. /24.9/
При додержанні цих умов будуть зрівноважені головний вектор сил інерції і головний момент пар сил інерції відносно осей х і у . Головний момент сил інерції відносно осі z, перпендикулярної до площини руху механізму, зрівноважується моментом рушійних сил і сил опору на головному валі машини.
У практиці машинобудування при зрівноважуванні механізмів умови /24.8/ і /24.9/ звичайно виконуються тільки частково.
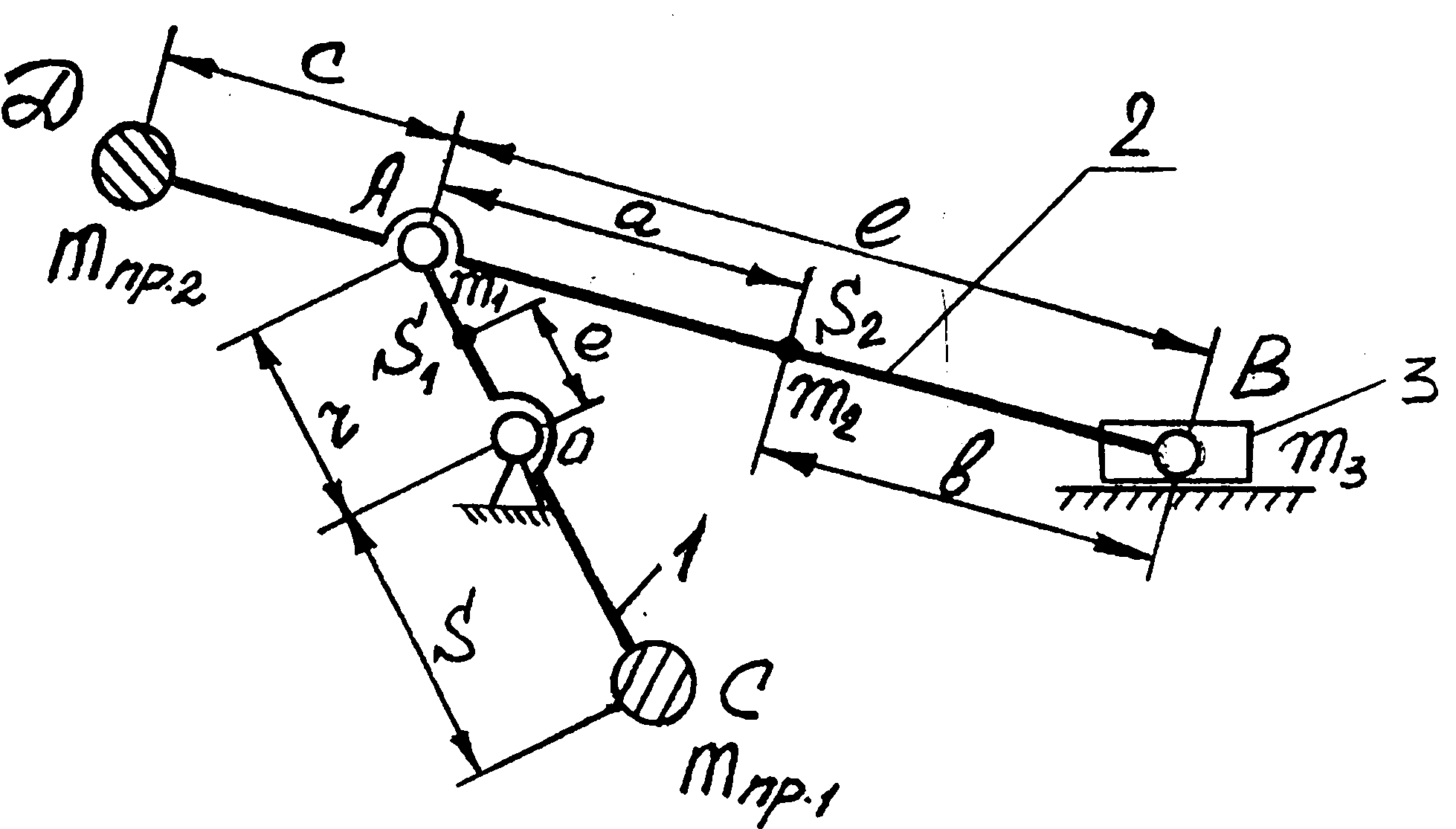
Нехай, наприклад, треба зрівноважити тільки головний вектор сил інерції кривошипно-повзунного механізму /рис. 24.4/. Позначимо маси кривошипа 1, шатуна 2 і повзуна 3 через m1, m2 і m3 і вважатимемо, що вони зосереджені відповідно в центрах мас S1 і S2 і В ланок. На лінії АВ в точці D встановлюємо противагу і визначаємо її масу mnp2 з умови, щоб центр мас mnp2, m2 i m3 збігався з точкою А.
Кривошипно-повзунний
механізм
Рис.24.4.
Складемо рівняння статичних моментів відносно точки А
m3L + m2a = mnp2C, /24.10/
звідки маємо:
/24.11/
Масу mnp1, противаги, яку встановлено в точці C кривошипа, визначаємо з умови, щоб центр мас mnp1, m1 і mA збігався з точкою D.
Повна маса в точці А буде:
mA = mnp2 + m2+ m3 /24.12/
Складемо рівняння статичних моментів відносно точки D
mAr + m1e = mnp1 S , /24.13/
звідки маємо:
/24.14/
Таким чином, дві противаги mnp1 і mnp2 цілком зрівноважують усі сили інерції даного механізму. Проте таке повне зрівноважування результуючої сили інерції кривошипно-повзунних механізмів на практиці застосовується рідко, бо при малому значенні радіуса S маса mnp2 буде дуже великою, внаслідок чого в кінематичних парах і ланках механізму виникнуть додаткові навантаження. При великому значенні радіуса S дуже збільшуються габарити всього механізму. Через те часто обмежуються лише наближеним зрівноважуванням механізмів. На практиці часто застосовують зрівноважування тільки маси кривошипа і частини маси шатуна.
24.4. Статичне і динамічне балансування обертових тіл.
Розрізняють два роди балансування: статичне і динамічне. Обертове тіло буде статично збалансоване, коли центр маси тіла лежатиме на осі обертання.
Щоб збалансувати тіло статично, його ставлять цапфами на дві паралельні лінійки /рис.24.5/.
У зв'язку з тим, що центр мас тіла лежить на осі, яка віддалена від осі обертання тіла на відстані rS, то сила ваги тіла намагатиметься повернути його в таке положення, при якому його центр мас стане в найнижче положення. Підбираючи додатковий тягар, розміщений на плечі r від осі обертання, завжди можна добитись стану байдужої рівноваги тіла на лінійках. Умова статично збалансованого тіла
/24.15/
Статичне
балансування
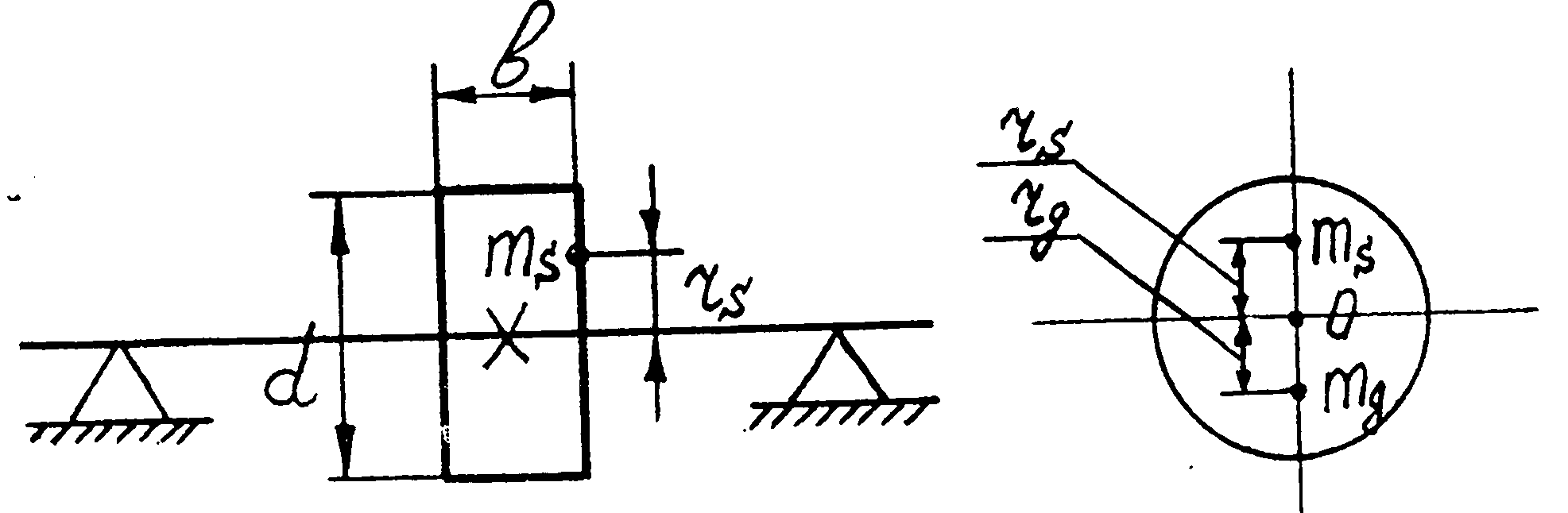
Рис.24.5.
Статичне балансування проводиться для роторів, в яких ширина о набагато менша діаметра d, в ≤ 0.2d, а також тіл обертання з невеликою кутовою швидкістю n< 200 об/хв.
Для барабанів, усяких роторів, коліс автомобіля, які мають значну кутову швидкість, необхідне динамічне балансування, бо навіть незначний дисбаланс створює великі динамічні зусилля на підшипники. Вісь обертання динамічно збалансованого тіла стає головною центральною віссю інерції. У цьому випадку головний вектор і головний момент пар сил інерції обертового тіла дорівнює нулю, тобто:
/24.16/
Установки /рис.24.6/, призначені для виявлення динамічної неврівноваженості тіла, дають можливість одночасно виявити і його статичну незрівноваженість.
Найпростішими установками для динамічного балансування є колискові, які грунтуються на принципі встановлення деталі, що балансується на пружну основу /колиска на пружинах/. У таких установках деталі що балансуються надається число обертів, близьке до резонансних. Тоді незрівноважені сили створюють значні амплітуди коливань, які фіксуються за допомогою приладів. Результати обчислень дають можливість визначити величину дисбалансу і місця його встановлення. Відомий балансуючий стенд Шитікова.
Стенд для балансування
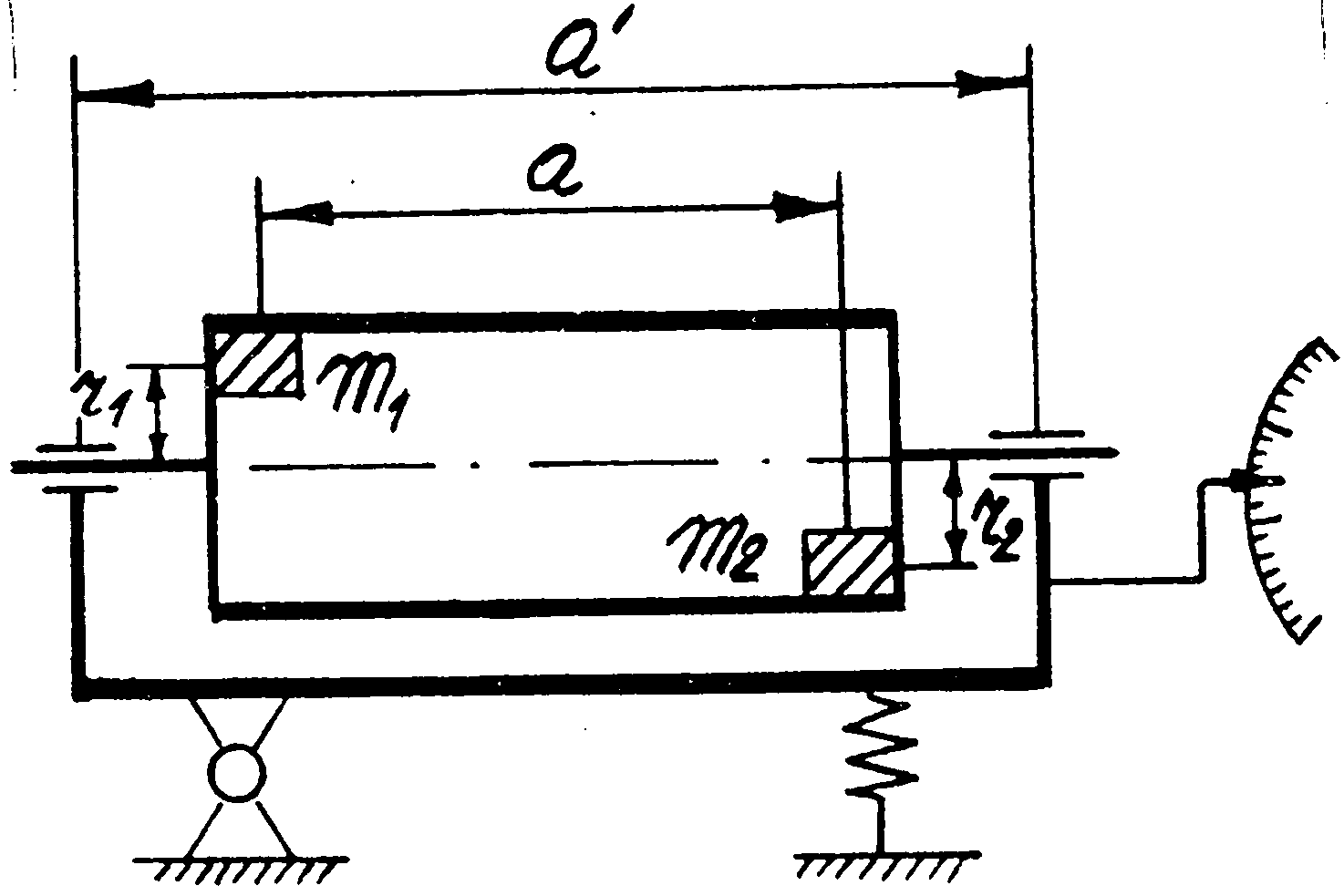
Рис.24.6.