З убчасте зачеплення

Рис.11.2

Швидкість т. К, що належить колесу 2 перпендикулярна радіусу 0₂К рівна

/11.4/

Проведемо через т.К загальну дотичну Т-Т і загальну нормаль N-N. Відмітимо т. Р перетину цієї нормалі з лінією центрів 0₁0₂. Із центрів 0₁і 0₂ опустимо перпендикуляри на нормаль N-N, отримаємо точки L₁ та L₂.

Ш видкість Vk1 розкладемо на два напрямки: по N-N і по Т-Т. Нормальна складова швидкості /11.5/

А налогічно отримаємо:

/11.6/

Д ля того, щоб зуби коліс не відходили один від одного і не врізались один в другий потрібно, щоб нормальні складові швидкостей і були рівні між собою за величиною і мали однаковий напрям

/11.7/

Підставимо в /11.7/ значення із /11.5/ і /11.6/, отримаємо:

ω₁O₁L₁=ω₂O₂L₂. /11.8/

З відси маємо:

/11.9/

Я кщо трикутники О₁ і L₁P і O₂ L₂P подібні, то можна записати:

. /11.10/

З амінивши відношення в /11.9/ із /11.10/ отримаємо:

/11.11/

З рівняння /11.11/ випливає формулювання основної теореми зачеплення – теорема Вілліса.

Загальна нормаль до профілів зубів в точці їх дотику ділить віддаль між центрами обертання зубчастих коліс на частини, обернено пропорційні їх кутовим швидкостям.

Точка Р називається полюсом зачеплення. При ω₁/ω₂=coпst, на основі /11.11/ знаходимо, що 0₂Р/0₁Р = coпst, тобто полюс зачеплення т.Р на лінії центрів займає стале положення. У випадку передачі обертального руху з сталим відношенням кутових швидкостей, профілі зубів повинні бути підібрані так, щоб загальна нормаль до них в будь – якій точці дотику К завжди проходила через одну і ту ж точку на лінії центрів.

11.2 Евольвента кола та її властивості.

Евольвентою кола – називається крива, яку описує будь – яка точка прямої лінії, що котиться по колу без ковзання. Це коло називається основним, а пряма, що перекочується по колу твірною, або виробляючою прямою /рис. 11.3/.

Нехай пряма N-N котиться по основному колу радіуса rь без ковзання. Точка К описує евольвенту. Біжучий радіус – вектор точки Кх

е вольвенти позначимо r_x. Початковий радіус – вектор евольвенти Ok_o=r_b. Гострий кут між дотичною до евольвенти в точці К_х і її радіусом – вектором Ок_х позначимо α_x. Кут О_х між початковим радіусом – вектором евольвенти Ок_о і її біжучим радіусом Ок_х, називається евольвент ним кутом або інволютою кута α_x, тобто /11.12/

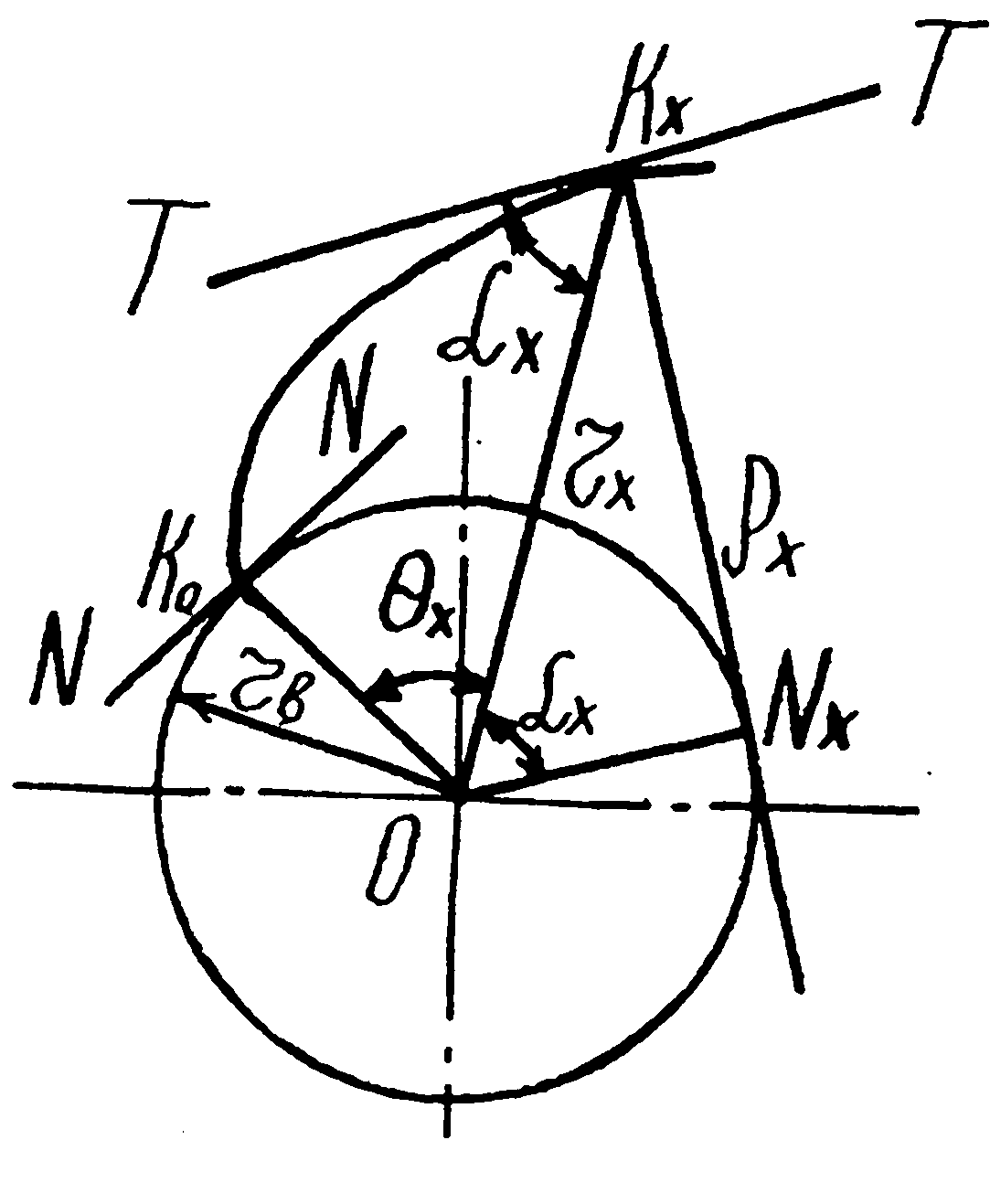Евольвента кола

Рис.11.3

Б удь – яка точка евольвенти визначається радіусом-вектора r_x і евольвент ним кутом θ_х. Оскільки пряма N-N котиться по основному колу без ковзання, то можна скласти рівність /11.13/

Із прямокутного трикутника Ok_xN_x маємо:

/11.14/

Знайдемо дуги знайдемо:

/11.15/ Підставимо значення із /11.14/ і /11.15/ в /11.13/, отримаємо:

r_b tgα_x=r_b(θ_x+α_x). /11.16/ Розділимо обидві частини рівняння /11.16/ на r_b, отримаємо:

θ_x+α_x=tgα_x, або

θ_x=tgα_x-α_x. /11.17/

Використавши позначення в рівнянні /11.12/, отримаємо

inVα_x=tgα_x-α_x, або

O_x=tgα_x-α_x=inVα_x. /11.18/

Зв’язок між r_x і £_x запишемо із трикутника K_xON_x

r_x= . /11.19/

Рівняння /11.18/ і /11.19/ називаються параметричними рівняннями евольвенти.

Властивості евольвенти:

1/ евольвента – симетрична крива, яка має дві вітки, що збігаються у початковій точці Ко;

2/ будь – які дотичні NN до основного кола є нормалями до евольвенти у відповідних точках Кх;

3/ основне коло є геометричним місцем центрів кривизна евольвент описаних прямою NN, тобто їх еволютою, а значить вектор KxNx є радіусом кривизна евольвенти у точці Кх.