
- •ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
- •ПРЕДИСЛОВИЕ К СЕРИИ
- •ОБ АВТОРЕ
- •СОДЕРЖАНИЕ
- •ПРЕДИСЛОВИЕ
- •БЛАГОДАРНОСТИ
- •ВВЕДЕНИЕ
- •ЧТО ТАКОЕ МОДЕЛЬ ЦВЕТОВОГО ВОСПРИЯТИЯ?
- •1.1 ОПТИКА ГЛАЗА
- •Роговица
- •Хрусталик
- •Жидкости
- •Радужная оболочка
- •Сетчатка
- •Центральная ямка сетчатки
- •Макула
- •Зрительный нерв
- •1.2 СЕТЧАТКА
- •Палочки и колбочки
- •1.3 ОБРАБОТКА ЗРИТЕЛЬНОГО СИГНАЛА
- •Рецептивные поля
- •1.4 МЕХАНИЗМЫ ЦВЕТОВОГО ЗРЕНИЯ
- •Трихроматическая теория
- •Оппонентная теория Геринга
- •Современная теория оппонентных цветов
- •Механизмы адаптации
- •Темновая адаптация
- •Световая адаптация
- •Хроматическая адаптация
- •Механизмы зрения, влияющие на цветовое восприятие
- •1.5 ПРОСТРАНСТВЕННЫЕ И ВРЕМЕННЫЕ СВОЙСТВА ЦВЕТОВОГО ЗРЕНИЯ
- •Эффект наклона
- •CSF и движения глаза
- •1.6 АНОМАЛИИ ЦВЕТОВОГО ЗРЕНИЯ
- •Протанопия, дейтеранопия и тританопия
- •Аномальные трихроматы
- •Аномалии цветового зрения и половая принадлежность
- •Отсев наблюдателей, выполняющих цветовые оценки
- •1.7 КЛЮЧЕВЫЕ МОМЕНТЫ В МОДЕЛИРОВАНИИ ЦВЕТОВОГО ВОСПРИЯТИЯ
- •2 ПСИХОФИЗИКА
- •2.1 ОПРЕДЕЛЕНИЕ ПСИХОФИЗИКИ
- •Два класса экспериментов со зрением
- •2.2 ИСТОРИЧЕСКАЯ СПРАВКА
- •Труды Вебера
- •Труды Фехнера
- •Труды Стивенса
- •2.3 КЛАССИФИКАЦИЯ ШКАЛ
- •Номинальные шкалы
- •Порядковые шкалы
- •Интервальные шкалы
- •Пропорциональные шкалы
- •Примеры использования шкал
- •2.4 ПОРОГОВЫЕ МЕТОДЫ
- •Виды пороговых экспериментов
- •Метод регулировки
- •Метод пределов
- •Метод постоянных стимулов
- •Метод «да — нет»
- •Метод принудительного выбора
- •Ступенчатые методы
- •Пробитовый анализ пороговых данных
- •2.5 МЕТОДЫ СРАВНЕНИЯ
- •Асимметричное соответствие
- •Сравнение по памяти
- •2.6 ОДНОМЕРНЫЕ ШКАЛЫ
- •2.7 МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ
- •2.8 ПОСТАНОВКА ПСИХОФИЗИЧЕСКИХ ЭКСПЕРИМЕНТОВ
- •2.9 ЗНАЧЕНИЕ ПСИХОФИЗИЧЕСКИХ ЭКСПЕРИМЕНТОВ
- •3 КОЛОРИМЕТРИЯ
- •3.1 БАЗОВАЯ И ВЫСШАЯ КОЛОРИМЕТРИИ
- •3.2 ПОЧЕМУ ЦВЕТ?
- •3.3 ИСТОЧНИКИ СВЕТА И ОСВЕТИТЕЛИ
- •Спектрорадиометрия
- •Абсолютно черные излучатели
- •3.4 ОКРАСКА МАТЕРИАЛЬНЫХ ОБЪЕКТОВ
- •Флуоресценция
- •3.5 ОТВЕТ ЗРИТЕЛЬНОЙ СИСТЕМЫ ЧЕЛОВЕКА
- •Фотометрическая система
- •3.6 ТРЕХСТИМУЛЬНЫЕ ЗНАЧЕНИЯ И ФУНКЦИИ ЦВЕТОВОГО СООТВЕТСТВИЯ
- •Трехстимульные значения любых стимулов
- •Усреднение функций цветового соответствия
- •Два комплекта функций цветового соответствия
- •3.7 ДИАГРАММЫ ЦВЕТНОСТЕЙ
- •3.8 ЦВЕТОВЫЕ ПРОСТРАНСТВА CIE
- •CIELAB
- •CIELUV
- •3.9 СПЕЦИФИКАЦИЯ ЦВЕТОВЫХ ОТЛИЧИЙ
- •3.10 СЛЕДУЮЩИЙ ШАГ
- •ПРИМЕЧАНИЕ ПЕРЕВОДЧИКА К ГЛАВЕ 3
- •4 ТЕРМИНОЛОГИЯ МОДЕЛЕЙ ЦВЕТОВОГО ВОСПРИЯТИЯ
- •4.1 ВАЖНОСТЬ ОПРЕДЕЛЕНИЙ
- •4.2 ЦВЕТ
- •4.3 ЦВЕТОВОЙ ТОН
- •4.4 СУБЪЕКТИВНАЯ ЯРКОСТЬ И СВЕТЛОТА
- •4.5 ПОЛНОТА ЦВЕТА И НАСЫЩЕННОСТЬ
- •4.6 ЧИСТОТА ЦВЕТА
- •4.7 ИЗОЛИРОВАННЫЕ И НЕИЗОЛИРОВАННЫЕ ЦВЕТА
- •4.8 ОПРЕДЕЛЕНИЯ В ВИДЕ ФОРМУЛ
- •4.9 СУБЪЕКТИВНАЯ ЯРКОСТЬ/ПОЛНОТА ПРОТИВ СВЕТЛОТЫ/НАСЫЩЕННОСТИ
- •5 ЦВЕТОВЫЕ КООРДИНАТНЫЕ СИСТЕМЫ
- •5.1 КРАТКИЙ ОБЗОР И ТРЕБОВАНИЯ
- •5.2 МАНСЕЛЛОВСКИЙ АТЛАС ЦВЕТОВ
- •Манселловская светлота
- •Манселловский цветовой тон
- •Манселловская насыщенность
- •Манселловский атлас цветов
- •5.3 ШВЕДСКАЯ СИСТЕМА ЕСТЕСТВЕННЫХ ЦВЕТОВ (NCS)
- •5.4 ЦВЕТОСПЕКТРАЛЬНАЯ КООРДИНАТНАЯ СИСТЕМА
- •5.5 ПРОЧИЕ КООРДИНАТНЫЕ СИСТЕМЫ
- •Равномерные цветовые шкалы OSA
- •Система Оствальда
- •5.6 ПРИМЕНЕНИЕ ЦВЕТОВЫХ КООРДИНАТНЫХ СИСТЕМ
- •Цветовые координатные системы в экспериментах со зрением
- •Цветовые координатные системы в живописи и дизайне
- •Цветовые координатные системы и обмен информацией о цвете
- •Цветовые координатные системы в образовании
- •Цветовые координатные системы в математической оценке моделей цветового восприятия
- •Цветовые координатные системы в системах визуализации изображений
- •Ограничения цветовых координатных систем
- •5.7 ЦВЕТОВЫЕ ИМЕННЫЕ СИСТЕМЫ
- •Пантонная система
- •Прочие системы
- •6 ФЕНОМЕНЫ ЦВЕТОВОГО ВОСПРИЯТИЯ
- •6.1 ЧТО ТАКОЕ ФЕНОМЕНЫ ЦВЕТОВОГО ВОСПРИЯТИЯ?
- •6.2 СИМУЛЬТАННЫЙ КОНТРАСТ, ОКОНТУРИВАНИЕ И СМАЗЫВАНИЕ
- •Симультанный контраст
- •Оконтуривание
- •Смазывание
- •6.3 ЭФФЕКТ БЕЦОЛЬДА — БРЮККЕ
- •6.4 ЭФФЕКТ ЭБНЕЯ
- •6.5 ЭФФЕКТ ГЕЛЬМГОЛЬЦА — КОЛЬРАУША
- •6.6 ЭФФЕКТ ХАНТА
- •6.7 ЭФФЕКТ СТИВЕНСА
- •6.8 ЭФФЕКТ ХЕЛЬСОНА — ДЖАДДА
- •6.9 ЭФФЕКТ БАРТЛЕСОНА — БРЕНЕМАНА
- •6.10 КОГНИТИВНОЕ ОБЕСЦВЕЧИВАНИЕ ОСВЕТИТЕЛЯ
- •6.11 ПРОЧИЕ КОНТЕКСТНЫЕ И СТРУКТУРНЫЕ ЭФФЕКТЫ
- •Двухцветные проекции
- •6.12 КОНСТАНТНОСТЬ ЦВЕТА?
- •7 УСЛОВИЯ ПРОСМОТРА
- •7.1 КОНФИГУРАЦИЯ ПОЛЯ ЗРЕНИЯ
- •Стимул
- •Проксимальное поле
- •Окружение
- •7.2 КОЛОРИМЕТРИЧЕСКАЯ СПЕЦИФИКАЦИЯ ПОЛЯ ЗРЕНИЯ
- •7.3 ЗРИТЕЛЬСКАЯ ИНТЕРПРЕТАЦИЯ
- •Интерпретация «Осветитель»
- •Интерпретация «Освещение»
- •Интерпретация «Поверхность»
- •Интерпретация «Объем»
- •Интерпретация «Пленка»
- •7.4 ЕЩЕ ОБ ИЗОЛИРОВАННЫХ И НЕИЗОЛИРОВАННЫХ ЦВЕТАХ
- •Изолированный цвет
- •Неизолированный цвет
- •8 ХРОМАТИЧЕСКАЯ АДАПТАЦИЯ
- •8.1 СВЕТОВАЯ, ТЕМНОВАЯ И ХРОМАТИЧЕСКАЯ АДАПТАЦИИ
- •Световая адаптация
- •Темновая адаптация
- •Хроматическая адаптация
- •8.2 ФИЗИОЛОГИЯ
- •Зрачковый рефлекс
- •Рецепторный контроль усиления
- •Субтрактивные механизмы
- •Высокоуровневые механизмы адаптации
- •Адаптация к движущимся стимулам
- •8.3 СЕНСОРНЫЕ И КОГНИТИВНЫЕ МЕХАНИЗМЫ
- •Сенсорные механизмы
- •Когнитивные механизмы
- •Твердая копия и экранное отображение
- •Временной аспект адаптации
- •8.4 СОГЛАСОВАННЫЕ ЦВЕТОВЫЕ СТИМУЛЫ
- •Асимметричное соответствие
- •Гаплоскопическое соответствие
- •Согласование по памяти
- •Величинная оценка
- •Сравнения по разным носителям
- •8.5 МОДЕЛИ
- •8.6 ВЫЧИСЛЕНИЕ ЦВЕТОВОЙ КОНСТАНТНОСТИ
- •9 МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ
- •9.1 МОДЕЛЬ ФОН КРИЗА
- •9.2 РЕТИНЕКСНАЯ ТЕОРИЯ
- •9.3 МОДЕЛЬ НАЯТАНИ
- •Модель Наятани
- •9.4 МОДЕЛЬ ГУТА
- •9.5 МОДЕЛЬ ФЕРШИЛЬДА
- •10 МОДЕЛИ ЦВЕТОВОГО ВОСПРИЯТИЯ
- •10.1 ОПРЕДЕЛЕНИЕ МОДЕЛЕЙ ЦВЕТОВОГО ВОСПРИЯТИЯ
- •10.2 СТРУКТУРА МОДЕЛЕЙ ЦВЕТОВОГО ВОСПРИЯТИЯ
- •10.3 CIELAB
- •Псевдофонкризовский расчет смены хроматической адаптации
- •10.4 ПОЧЕМУ НЕ ТОЛЬКО CIELAB?
- •10.5 ЧТО НАМ ДЕЛАТЬ С CIELUV?
- •11 МОДЕЛЬ НАЯТАНИ
- •11.1 ЦЕЛИ И ПОДХОД
- •11.2 ВХОДНЫЕ ДАННЫЕ
- •11.3 МОДЕЛЬ АДАПТАЦИИ
- •11.4 ОППОНЕНТНЫЕ ЦВЕТОВЫЕ РАЗМЕРНОСТИ
- •11.5 СУБЪЕКТИВНАЯ ЯРКОСТЬ
- •11.6 СВЕТЛОТА
- •11.7 ЦВЕТОВОЙ ТОН
- •11.8 ЧИСТОТА ЦВЕТА
- •11.9 НАСЫЩЕННОСТЬ
- •11.10 ПОЛНОТА ЦВЕТА
- •11.11 ОБРАТНАЯ МОДЕЛЬ
- •11.12 ПРОГНОЗИРОВАНИЕ ФЕНОМЕНОВ
- •11.13 ПОЧЕМУ НЕ ТОЛЬКО МОДЕЛЬ НАЯТАНИ?
- •12 МОДЕЛЬ ХАНТА
- •12.1 ЦЕЛИ И ПОДХОД
- •12.2 ВХОДНЫЕ ДАННЫЕ
- •12.3 МОДЕЛЬ АДАПТАЦИИ
- •12.4 ОППОНЕНТНЫЕ ЦВЕТОВЫЕ РАЗМЕРНОСТИ
- •12.5 ЦВЕТОВОЙ ТОН
- •12.6 ЧИСТОТА ЦВЕТА
- •12.7 СУБЪЕКТИВНАЯ ЯРКОСТЬ
- •12.8 СВЕТЛОТА
- •12.9 НАСЫЩЕННОСТЬ
- •12.10 ПОЛНОТА ЦВЕТА
- •12.11 ОБРАТНАЯ МОДЕЛЬ
- •12.12 ПРОГНОЗИРОВАНИЕ ФЕНОМЕНОВ
- •12.13 ПОЧЕМУ НЕ ТОЛЬКО МОДЕЛЬ ХАНТА?
- •13.1 ЦЕЛИ И ПОДХОД
- •13.2 ВХОДНЫЕ ДАННЫЕ
- •13.3 МОДЕЛЬ АДАПТАЦИИ
- •13.4 ОППОНЕНТНЫЕ ЦВЕТОВЫЕ РАЗМЕРНОСТИ
- •13.5 СВЕТЛОТА
- •13.6 ЦВЕТОВОЙ ТОН
- •13.7 НАСЫЩЕННОСТЬ
- •13.8 ЧИСТОТА ЦВЕТА
- •13.9 ОБРАТНАЯ МОДЕЛЬ
- •13.10 ПРОГНОЗИРОВАНИЕ ФЕНОМЕНОВ
- •13.11 ПОЧЕМУ НЕ ТОЛЬКО RLAB?
- •14 ПРОЧИЕ МОДЕЛИ
- •14.1 КРАТКИЙ ОБЗОР
- •14.2 МОДЕЛЬ ATD
- •Цели и подход
- •Входные данные
- •Модель адаптации
- •Оппонентные цветовые размерности
- •Корреляты восприятия
- •Предсказание феноменов
- •14.3 МОДЕЛЬ LLAB
- •Цели и подход
- •Входные данные
- •Модель адаптации
- •Оппонентные цветовые размерности
- •Корреляты восприятия
- •Цветовые отличия
- •Прогнозирование феноменов
- •15 МОДЕЛЬ CIECAM97s
- •15.1 ИСТОРИЯ ВОЗНИКНОВЕНИЯ, ЦЕЛИ И ПОДХОД
- •15.2 ВХОДНЫЕ ДАННЫЕ
- •15.3 МОДЕЛЬ АДАПТАЦИИ
- •15.4 КОРРЕЛЯТЫ ВОСПРИЯТИЯ
- •15.5 ОБРАТНАЯ МОДЕЛЬ
- •15.6 ПРОГНОЗИРОВАНИЕ ФЕНОМЕНОВ
- •Входные данные
- •Хроматическая адаптация
- •Корреляты восприятия
- •Обратная модель
- •15.8 ПОЧЕМУ НЕ ТОЛЬКО CIECAM97s?
- •16 МОДЕЛЬ CIECAM02
- •16.1 ЦЕЛИ И ПОДХОД
- •16.2 ВХОДНЫЕ ДАННЫЕ
- •16.3 МОДЕЛЬ АДАПТАЦИИ
- •Примечание к расчету смены хроматической адаптации в CIECAM02
- •Оставшаяся часть модели адаптации, задействованной в CIECAM02
- •16.4 ОППОНЕНТНЫЕ ЦВЕТОВЫЕ РАЗМЕРНОСТИ
- •16.5 ЦВЕТОВОЙ ТОН
- •16.6 СВЕТЛОТА
- •16.7 СУБЪЕКТИВНАЯ ЯРКОСТЬ
- •16.8 НАСЫЩЕННОСТЬ
- •16.9 ПОЛНОТА ЦВЕТА
- •16.10 ЧИСТОТА ЦВЕТА
- •16.11 ДЕКАРТОВЫ КООРДИНАТЫ
- •16.12 ОБРАТНАЯ МОДЕЛЬ
- •16.13 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ
- •16.14 ПРОГНОЗИРОВАНИЕ ФЕНОМЕНОВ
- •16.15 ПОЧЕМУ НЕ ТОЛЬКО CIECAM02?
- •16.16 ДАЛЬНЕЙШЕЕ РАЗВИТИЕ
- •17 ТЕСТИРОВАНИЕ МОДЕЛЕЙ ЦВЕТОВОГО ВОСПРИЯТИЯ
- •17.1 КРАТКИЙ ОБЗОР
- •17.2 КАЧЕСТВЕННАЯ ОЦЕНКА
- •17.3 ОЦЕНКА ПО СОГЛАСОВАННЫМ ЦВЕТОВЫМ СТИМУЛАМ
- •17.4 ОЦЕНКА ПУТЕМ КОЛИЧЕСТВЕННЫХ ЭКСПЕРИМЕНТОВ
- •17.5 НЕПОСРЕДСТВЕННОЕ ИСПЫТАНИЕ МОДЕЛЕЙ
- •17.6 ДЕЯТЕЛЬНОСТЬ CIE
- •17.7 ВИЗУАЛЬНАЯ ОЦЕНКА МОДЕЛЕЙ ЦВЕТОВОГО ВОСПРИЯТИЯ
- •18 ЦЕЛЕВОЕ НАЗНАЧЕНИЕ МОДЕЛЕЙ ЦВЕТОВОГО ВОСПРИЯТИЯ
- •18.1 ЦВЕТОПЕРЕДАЧА ИСТОЧНИКОВ ОСВЕЩЕНИЯ
- •Методы и рекомендации
- •Применение моделей цветового восприятия
- •Перспективы развития
- •18.2 ЦВЕТОВЫЕ ОТЛИЧИЯ
- •Методы и рекомендации
- •Применение моделей цветового восприятия
- •Перспективы развития
- •18.3 ИНДЕКСЫ МЕТАМЕРИЗМА
- •Методы и рекомендации
- •Применение моделей цветового восприятия
- •Перспективы развития
- •18.4 ЕДИНАЯ КОЛОРИМЕТРИЧЕСКАЯ СИСТЕМА?
- •19.1 СУТЬ ПРОБЛЕМЫ
- •19.2 УРОВНИ ЦВЕТОВОСПРОИЗВЕДЕНИЯ
- •1. Спектральное цветовоспроизведение
- •2. Колориметрическое цветовоспроизведение
- •3. Точное цветовоспроизведение
- •4. Эквивалентное цветовоспроизведение
- •5. Согласованное цветовоспроизведение
- •6. Выделенное цветовоспроизведение
- •19.3 МОДИФИЦИРОВАННЫЙ НАБОР УРОВНЕЙ ЦВЕТОВОСПРОИЗВЕДЕНИЯ
- •1. Произвольное цветовоспроизведение
- •3. Колориметрическое цветовоспроизведение
- •4. Цветовоспроизведение по восприятию
- •5. Приоритетное цветовоспроизведение
- •19.4 ОБЩАЯ СХЕМА
- •19.5 КАЛИБРОВКА И ХАРАКТЕРИЗАЦИЯ УСТРОЙСТВ
- •Три подхода к характеризации устройств
- •Характеризация путем физического моделирования
- •Характеризация путем эмпирического моделирования
- •Характеризация путем полного измерения
- •Виды колориметрических измерений
- •Блик, метамеризм осветителя и флуоресценция
- •Блик
- •Метамеризм осветителя
- •Флуоресценция
- •19.6 ПОТРЕБНОСТЬ В МОДЕЛЯХ ЦВЕТОВОГО ВОСПРИЯТИЯ
- •19.7 УСЛОВИЯ ПРОСМОТРА
- •19.8 ПРОСМОТРО%НЕЗАВИСИМОЕ ЦВЕТОВОЕ ПРОСТРАНСТВО
- •19.10 ЦВЕТОВЫЕ ПРИОРИТЕТЫ
- •Культурологические акценты приоритетного цветовоспроизведения
- •19.11 ОБРАТНЫЙ ПРОЦЕСС
- •19.12 ОБРАЗЦОВАЯ СИСТЕМА
- •Пространство связи профайлов
- •20 МОДЕЛИ ВОСПРИЯТИЯ ИЗОБРАЖЕНИЙ КАК МОДЕЛИ БУДУЩЕГО
- •20.1 ОТ ЦВЕТОВОГО ВОСПРИЯТИЯ К ВОСПРИЯТИЮ ИЗОБРАЖЕНИЙ
- •Колориметрия изображений
- •Уравнения цветовых отличий
- •Отличие изображений
- •Цветовое восприятие
- •Восприятие изображений и их качество
- •Модели цветового восприятия и модели восприятия изображений
- •20.3 МОДЕЛЬ ОТЛИЧИЯ ИЗОБРАЖЕНИЙ
- •Блок пространственной фильтрации
- •Блок пространственной локализации
- •Блок детекции локального контраста
- •Карта цветовых отличий
- •20.4 ВОСПРИЯТИЕ ИЗОБРАЖЕНИЙ И ИХ ВИЗУАЛИЗАЦИЯ
- •Шкалы восприятия
- •Оценка цветовых отличий
- •Симультанный контраст
- •Оконтуривание
- •Смазывание
- •20.5 МЕТРИКА ОТЛИЧИЙ И МЕТРИКА КАЧЕСТВА ИЗОБРАЖЕНИЙ
- •20.6 ТЕКУЩЕЕ ПОЛОЖЕНИЕ ДЕЛ И НАПРАВЛЕНИЯ РАЗВИТИЯ
- •Единая модель цветового восприятия?
- •Прочие модели цветового восприятия
- •Текущее научное тестирование моделей
- •Текущее положение дел
- •Общая схема действий
- •ЛИТЕРАТУРА

9 МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ
Хроматическая адаптация — это одно из важнейших свойств зрительной системы человека, которое мы обязательно должны понять, поскольку оно имеет непосредственное отношение к моделированию цветового воспри
ятия. В науке о зрении значение хроматической адаптации непреходяще, и по различным аспектам данной темы опубликовано множество работ.
В предыдущей главе были рассмотрены некоторые наиболее важные свойст ва и механизмы феномена адаптации, а также в ней была дана общая схема мо дели хроматической адаптации, прогнозирующий согласованные цветовые стимулы. В текущей главе детально описываются отдельные виды расчетов смены хроматической адаптации, но, конечно, все существующие модели, дан ные о которых когда либо публиковались, описать невозможно. Поэтому мы рассмотрим лишь некоторые из этих моделей и опишем фундаментальные взаимоотношения между ними. Читатели, заинтересованные в углубленном исследовании вопроса, а также интересующиеся историческим аспектом моде лей цветового восприятия могут обратиться к следующей литературе:
1.Cсылки, данные в 8 й главе (Бартлесон 1978, Терстиге 1972, Райт 1981, Ленни и Д`Змура 1988).
2.Ранняя история моделей хроматической адаптации: исследования Хель сона, Джадда и Варрена (1952), а также монография Вышецкого (1986), по священная вопросам цветового восприятия в целом и хроматической адапта ции в частности.
3.Классические работы по данной теме можно найти в сборнике, выпущен ном под редакцией Мак Адама (1993).
Отметим, что модели хроматической адаптации, описанные в текущей гла ве, хоть и позволяют вычислять согласованные цветовые стимулы, но при этом не являются моделями цветового восприятия, поскольку не оперируют пре дикторами его атрибутов, то есть величинами светлоты, насыщенности и цве тового тона. В то же время, модели вполне пригодны для прогноза цветовых со ответствий при изменении условий просмотра. Таким образом, модели хрома тической адаптации — это серьезное расширение трехстимульной колоримет рии, востребованное во многих областях науки и промышленности, и основа всех существующих сегодня моделей цветового восприятия.
Любая физиологически правдоподобная модель хроматической адаптации должна работать с сигналами, представляющими колбочковые ответы (или, по крайней мере, относительные колбочковые ответы). Таким образом, в приложе ниях, для которых критично использование CIE трехстимульной колоримет рии, прежде всего необходимо выполнить преобразование CIE трехстимульных значений (XYZ) в колбочковые ответы (обозначаемые как LMS, RGB или —
203
Г Л А В А 9 |
|
|
|
|
|
МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
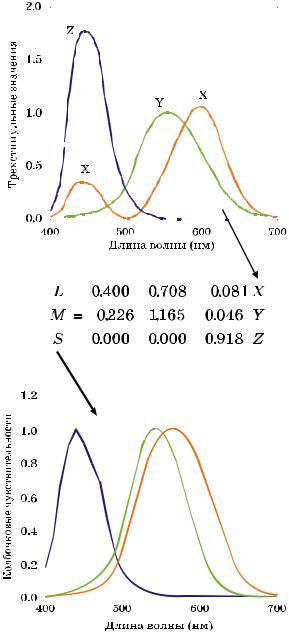
Рис. 9.1 Процесс линейного матричного преобразования трехстимульных значений XYZ
вLMS колбочковые чувствительности.
взависимости от той или иной конкретной модели). К счастью, колбочковые от
веты можно с высокой точностью рассчитать путем линейного преобразования CIE трехстимульных значений. Пример такого преобразования показан на рис. 9.1. Данное преобразование (или подобное ему) типично для всех моделей хроматической адаптации и всех моделей цветового восприятия, совместимых с CIE колориметрией, поэтому мы не будем подробно описывать его всякий раз, когда будем говорить о той или иной модели. Специфические преобразования, касающиеся эксклюзивных моделей, разумеется, будут обсуждаться отдельно.
204
Г Л А В А 9 |
МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ |
9.1 МОДЕЛЬ ФОН КРИЗА
Все действующие современные модели хроматической адаптации концепту ально и математически уходят корнями к идеям Иоганнеса фон Криза (1902). В свое время Фон Криз высказал ряд гипотез, которые сегодня переживают воз рождение: ученый предложил простую модель хроматической адаптации, явившуюся отправной точкой для будущих исследований. Сам фон Криз от сво их идей не ждал особого результата, о чем свидетельствует цитата из его работы от 1902 года (английский перевод Мак Адама):
«Если когда нибудь станет возможно объективным путем отделять друг от друга различные световые эффекты, то есть за счет непосредственного на блюдения за сетчаткой, то, наверное, потомки со снисходительной улыбкой вспомнят о наших усилиях и том долгом пути, на котором мы искали объяс нение тем же самым явлениям».
Спустя более чем девяносто лет мы оглядываемся на работу фон Криза без всякой «снисходительной улыбки», более того, мы восхищаемся тем, как бле стяще идеи фон Криза выдержали испытание временем.
На самом деле Фон Криз (1902) не предлагал специфического набора уравне ний, который сегодня именуют «моделью фон Криза», «законом фонкризовской пропорциональности», «законом фонкризовских коэффициентов» и пр. Свои гипотезы он выразил лишь словесно:
«Можно полагать, что отдельные компоненты органа зрения полностью не зависимы друг от друга и каждый утомлен или адаптирован исключительно в рамках своей функции».
Принято считать, что идеи фон Криза — это распространение грассманов ских законов аддитивного смешения цветовых стимулов на ситуацию перехода от одних условий просмотра к другим.
Современное толкование гипотез фон Криза в контексте моделей хроматиче ской адаптации выражено уравнениями 9.1–9.3:
La |
kL L |
(9.1) |
Ma kM M |
(9.2) |
|
Sa |
kS S |
(9.3) |
где L, M и S — это исходные колбочковые ответы; kL, kM и kS — коэффициенты шкалирования исходных колбочковых сигналов (то есть контроль усиления); La, Ma и Sa — постадаптационные колбочковые сигналы.
Уравнения 9.1–9.3 — это простая модель хроматической адаптации, осно ванная на том, что каждый из трех типов колбочек имеет персональный коэф фициент контроля усиления.
Ключевым аспектом подобных моделей является получение специфических
205

Г Л А В А 9 |
МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ |
значений kL, kM и kS. В большинстве современных интерпретаций фонкризов ской модели коэффициенты получены путем инверсии L , M и S колбочковых ответов на белый (или максимально яркий) стимул данной сцены, что демонст рируют уравнения 9.4–9.6:
kL 1/ Lна max |
или kL 1/ Lна белый |
(9.4) |
kM 1/ Mна max или kM 1/ Mна белый |
(9.5) |
|
kS 1/ Sна max |
или kS 1/ Sна белый |
(9.6) |
Уравнения 9.4–9.6 — это математическое представление фонкризовского тезиса о том, что «каждый утомлен или адаптирован исключительно в рамках своей функции». Вышеупомянутая интерпретация фонкризовских коэффици ентов усиления может быть использована при вычислении согласованных цве товых стимулов для двух разных условий просмотра путем расчета постадапта ционных сигналов для первых условий, последующей установки равенства с постадаптационными сигналами для вторых условий просмотра и финальной инверсии модели для вторых условий (формулы 9.7–9.9):
L2 |
(L1 / Lна max1)Lна max2 |
(9.7) |
M2 (M1 / Mна max1)Mна max2 |
(9.8) |
|
S2 |
(S1 / Sна max1)Sна max2 |
(9.9) |
В ряде случаев модель хроматической адаптации удобнее выражать в виде матричных преобразований. Матричную интерпретацию фонкризовской моде ли демонстрирует уравнение 9.10:
La |
|
1/ Lна max |
0.0 |
0.0 |
L |
|
Ma |
|
0.0 |
1/ Mна max |
0.0 |
M |
(9.10) |
Sa |
|
0.0 |
0.0 |
1/ Sна max |
S |
|
В целях вычисления согласованных цветовых стимулов для двух разных ус ловий просмотра матричное представление можно расширить путем включе ния в него преобразования CIE трехстимульных значений XYZ в относитель ные колбочковые ответы LMS (М матрица):
X2 |
|
Lна max 2 |
|
0.0 |
0.0 |
1/ Lна max 1 |
0.0 |
0.0 |
|
X1 |
|
|
Y |
M 1 |
0.0 |
M |
на max 2 |
0.0 |
0.0 |
1/ M |
на max 1 |
0.0 |
M |
Y |
(9.11) |
2 |
|
|
|
|
|
|
|
|
1 |
|
||
Z2 |
|
0.0 |
|
0.0 |
Sна max 2 |
0.0 |
0.0 |
1/ Sна max 1 |
|
Z1 |
|
|
206
Г Л А В А 9 |
МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ |
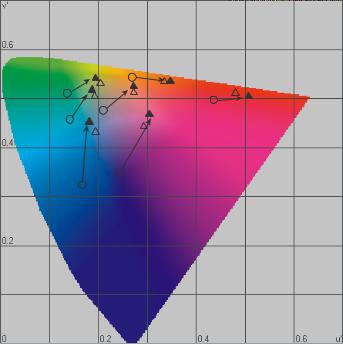
Рис. 9.2 Предикторы некоторых согласованных цветовых стимулов, полученные при помощи фонкризовской модели. Полые треугольнички представляют визуальные данные; сплошные треугольнички — предикторы модели.
Фонкризовский расчет смены хроматической адаптации при переходе от од них условий просмотра к другим использовался Бренеманом (1987) для про гнозирования визуальных данных его экспериментов (см. гл. 8). Результаты показаны на u` ` диаграмме цветностей (рис. 9.2): полые символы представля ют данные о бренемановских согласованных цветовых стимулах, а сплошные символы — это данные, спрогнозированные фонкризовской моделью. Заме тим, что прогнозы некоей идеальной модели были бы таковы, что сплошные треугольнички полностью совпали бы с полыми.
Внашем примере цветности стимулов при дневной адаптации (полые круж ки на рис. 9.2) были использованы для прогноза координат цветности согласо ванных стимулов при адаптации по свету ламп накаливания (треугольнички). Из рис. 9.2 ясно, что фонкризовская гипотеза в целом верна и что ее современ ное выражение в виде матричного расчета согласованных стимулов при смене хроматической адаптации прогнозирует эти стимулы на удивление хорошо.
Хельсон, Джадд и Варрен (1952) в свое время опубликовали исследование,
вкотором согласованные цветовые стимулы были получены путем сравнения по памяти, и фонкризовская гипотеза тогда очень хорошо справилась со своей задачей. Примеры и анализ результатов сравнительно недавних эксперимен тов, посвященных преимуществам и ограничениям фонкризовской гипотезы, можно найти в работе Брайнарда и Ванделла (1992), а также Чичильницкого и Ванделла (1995).
Вупомянутых экспериментах имеет место некоторое несоответствие между визуальными данными и предикторами фонкризовской модели — ученые пы
207
