530—Chapter 17. Time Series Regression
|
Modified Hannan-Quinn |
|
− 2 |
( l ⁄ T) + 2( k + τ)log ( log ( T) ) ⁄ T |
|
|
(MHQ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
where the modification factor τ is computed as: |
|
|
|
|
|
|
τ = α |
2 |
˜ 2 |
ˆ |
2 |
(17.61) |
|
|
|
Σ yt − 1 |
⁄ σu |
|
|
˜ |
|
|
|
t |
|
˜ |
|
|
|
|
|
|
|
|
as defined in “Autore- |
for yt = yt , when computing the ADF test equation, and for yt |
gressive Spectral Density Estimator” on page 528, when estimating f0 . NP (2001) propose and examine the modified criteria, concluding with a recommendation of the MAIC.
For the information criterion selection methods, you must also specify an upper bound to the lag length. By default, EViews chooses a maximum lag of:
kmax = int(12( T ⁄ 100)1 ⁄ 4) |
(17.62) |
See Hayashi (2000, p. 594) for a discussion of the selection of this upper bound.
Panel Unit Root Tests
Recent literature suggests that panel-based unit root tests have higher power than unit root tests based on individual time series. EViews will compute one of the following five types of panel unit root tests: Levin, Lin and Chu (2002), Breitung (2000), Im, Pesaran and Shin (2003), Fisher-type tests using ADF and PP tests (Maddala and Wu (1999) and Choi (2001)), and Hadri (1999).
While these tests are commonly termed “panel unit root” tests, theoretically, they are simply multiple-series unit root tests that have been applied to panel data structures (where the presence of cross-sections generates “multiple series” out of a single series). Accordingly, EViews supports these tests in settings involving multiple series: as a series view (if the workfile is panel structured), as a group view, or as a pool view.
Performing Panel Unit Root Tests in EViews
The following discussion assumes that you are familiar with the basics of both unit root tests and panel unit root tests.
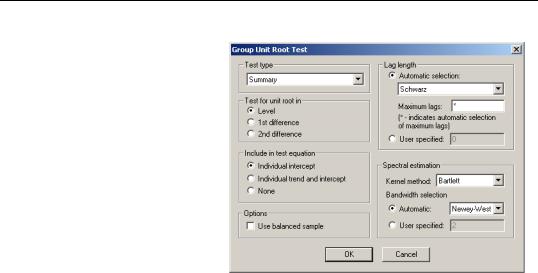
To begin, select View/Unit Root Test…from the menu of an EViews group or pool object, or from the menu of an individual series in a panel structured workfile. Here we show the dialog for a Group unit root test—the other dialogs differ slightly (for the pool object, there is an additional field in the upper-left hand portion of the dialog where you must indicate the name of the pool series on which you wish to conduct your test; for the series object in a panel workfile, the “balanced sample” option is not present).
Panel Unit Root Tests—531
If you wish to accept the default settings, simply click on OK. EViews will use the default Summary setting, and will compute a full suite of unit root tests on the levels of the series, along with a summary of the results.
To customize the unit root calculations, you will choose from a variety of options. The options on the left-hand side of the dialog determine the basic structure of the test or tests, while the options on the right-hand side of
the dialog control advanced computational details such as bandwidth or lag selection methods, or kernel methods.
The combo box at the top of the dialog is where you will choose the type of test to perform. There are six settings: “Summary”, “Common root - Levin, Lin, Chu”, “Common root - Breitung”, “Individual root - Im, Pesaran, Shin”, “Individual root - Fisher - ADF”, “Individual root - Fisher - PP”, and “Common root - Hadri”, corresponding to one or more of the tests listed above. The combo box labels include a brief description of the assumptions under which the tests are computed. “Common root” indicates that the tests are estimated assuming a common AR structure for all of the series; “Individual root” is used for tests which allow for different AR coefficients in each series.
We have already pointed out that the Summary default instructs EViews to estimate all of the tests, and to provide a brief summary of the results. Selecting an individual test type allows you better control over the computational method and provides additional detail on the test results.
The next two sets of radio buttons allow you to control the specification of your test equation. First, you may choose to conduct the unit root on the Level, 1st difference, or 2nd difference of your series. Next, you may choose between sets of exogenous regressors to be included. You can select Individual intercept if you wish to include individual fixed effects, Individual intercepts and individual trends to include both fixed effects and trends, or None for no regressors.
The Use balanced sample option is present only if you are estimating a Pool or a Group unit root test. If you select this option, EViews will adjust your sample so that only observations where all series values are not missing will be included in the test equations.
532—Chapter 17. Time Series Regression
Depending on the form of the test or tests to be computed, you will be presented with various advanced options on the right side of the dialog. For tests that involve regressions on lagged difference terms (Levin, Lin, and Chu, Breitung, Im, Pesaran, and Shin, Fisher - ADF) these options relate to the choice of the number of lags to be included. For the tests involving kernel weighting (Levin, Lin, and Chu, Fisher - PP, Hadri), the options relate to the choice of bandwidth and kernel type.
For a group or pool unit root test, the EViews default is to use automatic selection methods: information matrix criterion based for the number of lag difference terms (with automatic selection of the maximum lag to evaluate), and the Andrews or Newey-West method for bandwidth selection. For unit root tests on a series in a panel workfile, the default behavior uses user-specified options.
If you wish to override these settings, simply enter the appropriate information. You may, for example, select a fixed, user-specified number of lags by entering a number in the User specified field. Alternatively, you may customize the settings for automatic lag selection method. Alternative criteria for evaluating the optimal lag length may be selected via the combo box (Akaike, Schwarz, Hannan-Quinn, Modified Akaike, Modified Schwarz, Modified Hannan-Quinn), and you may limit the number of lags to try in automatic selection by entering a number in the Maximum lags box. For the kernel based methods, you may select a kernel type from the combo box (Bartlett, Parzen, Quadratic spectral), and you may specify either an automatic bandwidth selection method (Andrews, Newey-West) or user-specified fixed bandwidth.
As an illustration, we compute the summary panel unit root test, using individual fixed effects as regressors, and automatic lag difference term and bandwidth selection (using the Schwarz criterion for the lag differences, and the Newey-West method and the Bartlett kernel for the bandwidth). The results for the panel unit root test are presented below:
Panel Unit Root Tests—533
Panel unit root test: Summary
Date: 07/02/03 Time: 13:13
Sample: 1935 1954
Exogenous variables: Individual effects
Automatic selection of maximum lags
Automatic selection of lags based on SIC: 0 to 3
Newey-West bandwidth selection using Bartlett kernel
|
|
|
Cross- |
|
Method |
Statistic |
Prob.** |
sections |
Obs |
Null: Unit root (assumes common unit root process) |
|
|
Levin, Lin & Chu t* |
2.39544 |
0.9917 |
10 |
184 |
Breitung t-stat |
-2.06574 |
0.0194 |
10 |
174 |
Null: Unit root (assumes individual unit root process) |
|
|
Im, Pesaran and Shin W-stat |
2.80541 |
0.9975 |
10 |
184 |
ADF - Fisher Chi-square |
12.0000 |
0.9161 |
10 |
184 |
PP - Fisher Chi-square |
12.9243 |
0.8806 |
10 |
190 |
Null: No unit root (assumes common unit root process) |
|
|
Hadri Z-stat |
9.33436 |
0.0000 |
10 |
200 |
** Probabilities for Fisher tests are computed using an asymptotic Chi -square distribution. All other tests assume asymptotic normality.
The top of the output indicates the type of test, exogenous variables and test equation options. If we were instead estimating a Pool or Group test, a list of the series used in the test would also be depicted. The lower part of the summary output gives the main test results, organized both by null hypothesis as well as the maintained hypothesis concerning the type of unit root process. For example, we group the results for the LLC and the Breitung tests, since they both have a null of a unit root for the common process.
For the most part, the results indicate the presence of a unit root. The LLC, IPS, and both Fisher tests fail to reject the null of a unit root. Similarly, the Hadri test statistic, which tests the null of no unit root, strongly rejects the null in favor of a unit root. The one exception to this pattern is the Breitung test, which does reject the unit root null.
If you only wish to compute a single unit root test type, or if you wish to examine the tests results in greater detail, you may simply repeat the unit root test after selecting the desired test in Test type combo box. Here, we show the bottom portion of the LLC test specific output for the same data:
534—Chapter 17. Time Series Regression
Intermediate results on I
Cross |
2nd Stage |
Variance |
HAC of |
|
Max |
Band- |
|
section |
Coefficient |
of Reg |
Dep. |
Lag |
Lag |
width |
Obs |
|
|
|
|
|
|
|
|
1 |
-0.35898 |
147.58 |
11.767 |
1 |
4 |
18.0 |
18 |
2 |
-0.05375 |
444.60 |
236.40 |
0 |
4 |
7.0 |
19 |
3 |
-0.11741 |
0.8153 |
0.5243 |
0 |
4 |
5.0 |
19 |
4 |
-0.10233 |
408.12 |
179.68 |
3 |
4 |
5.0 |
16 |
5 |
0.22672 |
11314. |
18734. |
0 |
4 |
1.0 |
19 |
6 |
-0.26332 |
90.040 |
89.960 |
0 |
4 |
2.0 |
19 |
7 |
0.12362 |
62.429 |
82.716 |
0 |
4 |
1.0 |
19 |
8 |
-0.13862 |
129.04 |
22.173 |
0 |
4 |
17.0 |
19 |
9 |
-0.55912 |
7838.8 |
1851.4 |
1 |
4 |
11.0 |
18 |
10 |
-0.44416 |
113.56 |
43.504 |
1 |
4 |
6.0 |
18 |
|
Coefficient |
t-Stat |
SE Reg |
mu* |
sig* |
|
Obs |
|
|
|
|
|
|
|
|
Pooled |
-0.01940 |
-0.464 |
1.079 |
-0.554 |
0.919 |
|
184 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
For each cross-section, the autoregression coefficient, variance of the regression, HAC of the dependent variable, the selected lag order, maximum lag, bandwidth truncation parameter, and the number of observations used are displayed.
Panel Unit Root Details
Panel unit root tests are similar, but not identical, to unit root tests carried out on a single series. Here, we briefly describe the five panel unit root tests currently supported in EViews; for additional detail, we encourage you to consult the original literature. The discussion assumes that you have a basic knowledge of unit root theory.
We begin by classifying our unit root tests on the basis of whether there are restrictions on the autoregressive process across cross-sections or series. Consider a following AR(1) process for panel data:
yit = ρiyit − 1 + Xitδi + it |
(17.63) |
where i = 1, 2, …, N cross-section units or series, that are observed over periods t = 1, 2, …, Ti .
The Xit represent the exogenous variables in the model, including any fixed effects or individual trends, ρi are the autoregressive coefficients, and the errors it are assumed to be mutually independent idiosyncratic disturbance. If ρi < 1 , yi is said to be weakly (trend-) stationary. On the other hand, if ρi = 1 then yi contains a unit root.
For purposes of testing, there are two natural assumptions that we can make about the ρi . First, one can assume that the persistence parameters are common across cross-sections so
Panel Unit Root Tests—535
that ρi = ρ for all i . The Levin, Lin, and Chu (LLC), Breitung, and Hadri tests all employ this assumption. Alternatively, one can allow ρi to vary freely across cross-sec- tions. The Im, Pesaran, and Shin (IPS), and Fisher-ADF and Fisher-PP tests are of this form.
Tests with Common Unit Root Process
Levin, Lin, and Chu (LLC), Breitung, and Hadri tests all assume that there is a common unit root process so that ρi is identical across cross-sections. The first two tests employ a null hypothesis of a unit root while the Hadri test uses a null of no unit root.
LLC and Breitung both consider the following basic ADF specification:
pi |
|
∆yit = αyit − 1 + Σ βij∆yit − j + X′itδ + it |
(17.64) |
j = 1
where we assume a common α = ρ − 1 , but allow the lag order for the difference terms, pi , to vary across cross-sections. The null and alternative hypotheses for the tests may be written as:
H0: α = 0 |
(17.65) |
H1: α < 0 |
(17.66) |
Under the null hypothesis, there is a unit root, while under the alternative, there is no unit root.
Levin, Lin, and Chu
The method described in LLC derives estimates of α from proxies for ∆yit |
and yit that |
are standardized and free of autocorrelations and deterministic components. |
|
For a given set of lag orders, we begin by estimating two additional sets of equations, |
regressing both ∆yit , and yit − 1 on the lag terms ∆yit − j |
(for j = 1, …, pi ) and the |
exogenous variables X |
|
. The estimated coefficients from these two regressions will be |
ˆ ˆ |
· |
it· |
|
|
|
denoted ( β, δ) |
and ( β, δ) , respectively. |
|
|
|
|
|
|
by taking ∆yit and removing the autocorrelations and deterministic |
We define ∆y |
it |
components using the first set of auxiliary estimates: |
|
|
|
|
|
|
|
|
|
|
|
|
pi |
ˆ |
ˆ |
|
|
|
|
|
|
∆yit = ∆yit− Σ βij∆yit − j − X′itδ |
(17.67) |
|
|
|
|
|
|
|
|
|
j = 1 |
|
|
|
Likewise, we may define the analogous |
|
it − 1 using the second set of coefficients: |
y |
|
|
|
|
|
|
|
|
|
|
pi |
· |
· |
|
|
|
|
|
yit − 1 = yit − 1− Σ βij∆yit − j − |
X′itδ |
(17.68) |
536—Chapter 17. Time Series Regression
Next, we obtain our proxies by standardizing both ∆yit and yit − 1 , dividing by the regression standard error:
˜ |
|
|
|
|
|
|
|
|
= |
( ∆yit |
⁄ si) |
|
∆yit |
(17.69) |
˜ |
|
|
|
|
|
|
|
= |
( yit − 1 ⁄ si) |
|
yit − 1 |
|
where si are the estimated standard errors from estimating each ADF in Equation (17.64).
Lastly, an estimate of the coefficient α may be obtained from the pooled proxy equation:
|
|
|
˜ |
|
|
|
˜ |
|
+ ηit |
|
|
(17.70) |
|
|
|
∆yit = |
|
αyit − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
LLC show that under the null, a modified t-statistic for the resulting α is asymptotically |
normally distributed |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
˜ |
|
|
|
ˆ −2 |
|
ˆ |
|
|
˜ |
|
|
|
tα |
α |
− ( NT) S |
N |
σ |
se(α)µ |
|
|
|
|
|
|
|
|
|
|
|
mT |
→ N( 0, 1) |
(17.71) |
= -------------------------------------------------------------------- |
|
|
|
|
σ |
|
˜ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mT |
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
ˆ |
2 |
is the estimated variance of the error |
where tα is the standard t-statistic for α |
|
= 0 , σ |
|
ˆ |
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
term η , se(α) is the standard error of |
α , and: |
|
|
|
|
|
|
|
|
|
|
˜ |
|
|
|
|
|
|
|
|
|
|
|
(17.72) |
|
|
|
T = T − ( Σ pi ⁄ N) − 1 |
|
i
The remaining terms, which involve complicated moment calculations, are described in greater detail in LLC . The average standard deviation ratio, SN , is defined as the mean of the ratios of the long-run standard deviation to the innovation standard deviation for each individual. Its estimate is derived using kernel-based techniques. The remaining two
terms, µ ˜ |
and σ |
˜ |
are adjustment terms for the mean and standard deviation. |
mT |
|
mT |
|
The LLC method requires a specification of the number of lags used in each cross-section ADF regression, pi , as well as kernel choices used in the computation of SN . In addition, you must specify the exogenous variables used in the test equations. You may elect to include no exogenous regressors, or to include individual constant terms (fixed effects), or to employ individual constants and trends.
Breitung
The Breitung method differs from LLC in two distinct ways. First, only the autoregressive portion (and not the exogenous components) is removed when constructing the standardized proxies:
˜ |
|
pi |
ˆ |
|
⁄ si |
∆yit |
= |
∆yit− Σ βij∆yit − j |
|
|
j = 1 |
|
|
(17.73) |
|
|
pi |
|
|
˜ |
· |
⁄ si |
yit − 1 |
= yit − 1− Σ βij∆yit − j |
j = 1
Panel Unit Root Tests—537
ˆ |
· |
are as defined for LLC. |
|
|
|
|
where β , β , and si |
|
|
|
|
Second, the proxies are transformed and detrended, |
|
|
|
|
|
( T − t) |
|
|
˜ |
|
˜ |
|
˜ |
|
= |
|
− |
∆yit + 1 |
+ … + ∆yit + T |
|
∆yit |
(--------------------------T − t + 1) |
∆yit |
----------------------------------------------------------- |
T − t |
|
|
|
|
|
|
|
|
|
|
|
˜ |
|
|
|
|
|
|
|
|
yit − 1 |
= yit − 1 − cit |
|
|
|
|
|
|
|
where, |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
if no intercept or trend |
|
|
|
˜ |
|
|
|
|
with intercept, no trend |
|
cit = |
|
yi1 |
|
|
|
|
|
|
˜ |
− ( ( t − 1) ⁄ |
˜ |
|
|
with intercept and trend |
|
yi1 |
T )yiT |
|
|
The persistence parameter α is estimated from the pooled proxy equation:
∆y |
|
= |
αy |
+ ν |
it |
(17.76) |
|
it |
|
|
it − 1 |
|
Breitung shows that under the null, the resulting estimator α is asymptotically distributed as a standard normal.
The Breitung method requires only a specification of the number of lags used in each cross-section ADF regression, pi , and the exogenous regressors. As with the LLC test, you may elect to include no exogenous regressors, or to include individual constant terms (fixed effects), or individual constants and trends. Note that in contrast with LLC, no kernel computations are required.
Hadri
The Hadri panel unit root test is similar to the KPSS unit root test, and has a null hypothesis of no unit root in any of the series in the panel. Like the KPSS test, the Hadri test is based on the residuals from the individual OLS regressions of yit on a constant, or on a constant and a trend. For example, if we include both the constant and a trend, we derive estimates from:
yit = δi + ηit + it
Given the residuals ˆ from the individual regressions, we form the LM statistic:
|
1 |
|
|
|
|
|
2 |
|
2 |
|
|
|
LM1 |
|
|
|
|
Si( t) |
⁄ T |
⁄ f0 |
= ---- |
N |
Σ |
|
|
|
N |
Σi = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
where Si( t) are the cumulative sums of the residuals,
538—Chapter 17. Time Series Regression
and f0 is the average of the individual estimators of the residual spectrum at frequency zero:
i = 1
EViews provides several methods for estimating the fi0 . See “Unit Root Tests” on page 518 for additional details.
An alternative form of the LM statistic allows for heteroskedasticity across i :
LM |
|
1 |
N |
|
S |
( t) |
2 |
⁄ T |
2 |
⁄ f |
|
(17.81) |
|
= ---- |
Σi = 1 |
Σt |
|
|
i0 |
|
2 |
N |
|
i |
|
|
|
|
|
Hadri shows that under mild assumptions, |
|
|
|
|
|
|
|
|
|
|
|
|
N( LM − ξ) |
→ N( 0, 1 ) |
|
|
(17.82) |
|
Z = -------------------------------- |
|
|
|
|
|
ζ |
|
|
|
|
|
|
|
|
|
|
where ξ = 1 ⁄ 6 and ζ = 1 ⁄ 45 , if the model only includes constants (ηi is set to 0 for all i ), and ξ = 1 ⁄ 15 and ζ = 11 ⁄ 6300 , otherwise.
The Hadri panel unit root tests require only the specification of the form of the OLS regressions: whether to include only individual specific constant terms, or whether to include both constant and trend terms. EViews reports two Z -statistic values, one based on LM1 with the associated homoskedasticity assumption, and the other using LM2 that is heteroskedasticity consistent.
Tests with Individual Unit Root Processes
The Im, Pesaran, and Shin, and the Fisher-ADF and PP tests all allow for individual unit root processes so that ρi may vary across cross-sections. The tests are all characterized by the combining of individual unit root tests to derive a panel-specific result.
Im, Pesaran, and Shin
Im, Pesaran, and Shin begin by specifying a separate ADF regression for each cross section:
pi |
|
∆yit = αyit − 1 + Σ βij∆yit − j + X′itδ + it |
(17.83) |
j = 1 |
|
The null hypothesis may be written as, |
|
H0: αi = 0, for all i |
(17.84) |
while the alternative hypothesis is given by:
|
|
|
Panel Unit Root Tests—539 |
|
|
|
αi = 0 |
for i = 1, 2, …, N1 |
(17.85) |
H1: |
< 0 |
|
αi |
for i = N + 1, N + 2, …, N |
(where the i may be reordered as necessary) which may be interpreted as a non-zero fraction of the individual processes is stationary.
After estimating the separate ADF regressions, the average of the t-statistics for αi |
from |
the individual ADF regressions, tiTi ( pi ) : |
|
|
|
|
|
N |
|
⁄ N |
|
tNT = |
Σ tiTi |
( pi) |
(17.86) |
i = 1
is then adjusted to arrive at the desired test statistics.
In the case where the lag order is always zero ( pi = 0 for all i ), simulated critical values for tNT are provided in the IPS paper for different numbers of cross sections N , series lengths T , and for test equations containing either intercepts, or intercepts and linear trends. EViews uses these values, or linearly interpolated values, in evaluating the significance of the test statistics.
In the general case where the lag order in Equation (17.83) may be non-zero for some cross-sections, IPS show that a properly standardized tNT has an asymptotic standard normal distribution:
|
|
|
−1 |
N |
|
|
|
N tNT − N |
|
Σ E( tiT( pi) ) |
|
WtN T |
= |
|
|
i = 1 |
→ N( 0, 1 ) |
(17.87) |
N |
|
|
|
N−1 |
|
|
|
|
|
Σ Var( tiT( pi) ) |
|
|
i = 1
The expressions for the expected mean and variance of the ADF regression t-statistics,
E( tiT( pi) ) and Var( tiT( pi) ) , are provided by IPS for various values of T and p and differing test equation assumptions, and are not provided here.
The IPS test statistic requires specification of the number of lags and the specification of the deterministic component for each cross-section ADF equation. You may choose to include individual constants, or to include individual constant and trend terms.
Fisher-ADF and Fisher-PP
An alternative approach to panel unit root tests uses Fisher’s (1932) results to derive tests that combine the p-values from individual unit root tests. This idea has been proposed by Maddala and Wu, and by Choi.
If we define πi as the p-value from any individual unit root test for cross-section i , then under the null of unit root for all N cross-sections, we have the asymptotic result that
540—Chapter 17. Time Series Regression
|
|
N |
|
|
|
|
−2 Σ log ( πi) → χ22N |
(17.88) |
|
|
i = 1 |
|
|
|
In addition, Choi demonstrates that: |
|
|
|
|
|
1 |
N |
−1 |
( πi) → N( 0, 1) |
(17.89) |
Z |
= -------- Σ Φ |
|
|
Ni = 1 |
|
|
|
where Φ−1 is the inverse of the standard normal cumulative distribution function.
EViews reports both the asymptotic χ2 and standard normal statistics using ADF and Phil- lips-Perron individual unit root tests. The null and alternative hypotheses are the same as for the as IPS.
For both Fisher tests, you must specify the exogenous variables for the test equations. You may elect to include no exogenous regressors, to include individual constants (effects), or include individual constant and trend terms.
Additionally, when the Fisher tests are based on ADF test statistics, you must specify the number of lags used in each cross-section ADF regression. For the PP form of the test, you must instead specify a method for estimating f0 . EViews supports estimators for f0 based on kernel-based sum-of-covariances. See “Frequency Zero Spectrum Estimation” beginning on page 527 for details.
Summary of Available Panel Unit Root Tests
The following table summarizes the basic characteristics of the panel unit root tests available in EViews:
Test |
Null |
Alternative |
Possible |
Autocorrela- |
|
|
|
Deterministic |
tion Correc- |
|
|
|
Component |
tion Method |
|
|
|
|
|
Levin, Lin |
Unit root |
No Unit Root |
None, F, T |
Lags |
and Chu |
|
|
|
|
|
|
|
|
|
Breitung |
Unit root |
No Unit Root |
None, F, T |
Lags |
|
|
|
|
|
IPS |
Unit Root |
Some cross- |
F, T |
Lags |
|
|
sections with- |
|
|
|
|
out UR |
|
|
|
|
|
|
|
|
|
|
|
|
Panel Unit Root Tests—541 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fisher-ADF |
Unit Root |
Some cross- |
None, F, T |
Lags |
|
|
|
|
sections with- |
|
|
|
|
|
|
out UR |
|
|
|
|
|
|
|
|
|
|
|
Fisher-PP |
Unit Root |
Some cross- |
None, F, T |
Kernel |
|
|
|
|
sections with- |
|
|
|
|
|
|
out UR |
|
|
|
|
|
|
|
|
|
|
|
Hadri |
No Unit |
Unit Root |
F, T |
Kernel |
|
|
|
Root |
|
|
|
|
|
|
|
|
|
|
|
None - no exogenous variables; F - fixed effect; and T - individual effect and individual trend.
542—Chapter 17. Time Series Regression
