
- •Table of Contents
- •What’s New in EViews 5.0
- •What’s New in 5.0
- •Compatibility Notes
- •EViews 5.1 Update Overview
- •Overview of EViews 5.1 New Features
- •Preface
- •Part I. EViews Fundamentals
- •Chapter 1. Introduction
- •What is EViews?
- •Installing and Running EViews
- •Windows Basics
- •The EViews Window
- •Closing EViews
- •Where to Go For Help
- •Chapter 2. A Demonstration
- •Getting Data into EViews
- •Examining the Data
- •Estimating a Regression Model
- •Specification and Hypothesis Tests
- •Modifying the Equation
- •Forecasting from an Estimated Equation
- •Additional Testing
- •Chapter 3. Workfile Basics
- •What is a Workfile?
- •Creating a Workfile
- •The Workfile Window
- •Saving a Workfile
- •Loading a Workfile
- •Multi-page Workfiles
- •Addendum: File Dialog Features
- •Chapter 4. Object Basics
- •What is an Object?
- •Basic Object Operations
- •The Object Window
- •Working with Objects
- •Chapter 5. Basic Data Handling
- •Data Objects
- •Samples
- •Sample Objects
- •Importing Data
- •Exporting Data
- •Frequency Conversion
- •Importing ASCII Text Files
- •Chapter 6. Working with Data
- •Numeric Expressions
- •Series
- •Auto-series
- •Groups
- •Scalars
- •Chapter 7. Working with Data (Advanced)
- •Auto-Updating Series
- •Alpha Series
- •Date Series
- •Value Maps
- •Chapter 8. Series Links
- •Basic Link Concepts
- •Creating a Link
- •Working with Links
- •Chapter 9. Advanced Workfiles
- •Structuring a Workfile
- •Resizing a Workfile
- •Appending to a Workfile
- •Contracting a Workfile
- •Copying from a Workfile
- •Reshaping a Workfile
- •Sorting a Workfile
- •Exporting from a Workfile
- •Chapter 10. EViews Databases
- •Database Overview
- •Database Basics
- •Working with Objects in Databases
- •Database Auto-Series
- •The Database Registry
- •Querying the Database
- •Object Aliases and Illegal Names
- •Maintaining the Database
- •Foreign Format Databases
- •Working with DRIPro Links
- •Part II. Basic Data Analysis
- •Chapter 11. Series
- •Series Views Overview
- •Spreadsheet and Graph Views
- •Descriptive Statistics
- •Tests for Descriptive Stats
- •Distribution Graphs
- •One-Way Tabulation
- •Correlogram
- •Unit Root Test
- •BDS Test
- •Properties
- •Label
- •Series Procs Overview
- •Generate by Equation
- •Resample
- •Seasonal Adjustment
- •Exponential Smoothing
- •Hodrick-Prescott Filter
- •Frequency (Band-Pass) Filter
- •Chapter 12. Groups
- •Group Views Overview
- •Group Members
- •Spreadsheet
- •Dated Data Table
- •Graphs
- •Multiple Graphs
- •Descriptive Statistics
- •Tests of Equality
- •N-Way Tabulation
- •Principal Components
- •Correlations, Covariances, and Correlograms
- •Cross Correlations and Correlograms
- •Cointegration Test
- •Unit Root Test
- •Granger Causality
- •Label
- •Group Procedures Overview
- •Chapter 13. Statistical Graphs from Series and Groups
- •Distribution Graphs of Series
- •Scatter Diagrams with Fit Lines
- •Boxplots
- •Chapter 14. Graphs, Tables, and Text Objects
- •Creating Graphs
- •Modifying Graphs
- •Multiple Graphs
- •Printing Graphs
- •Copying Graphs to the Clipboard
- •Saving Graphs to a File
- •Graph Commands
- •Creating Tables
- •Table Basics
- •Basic Table Customization
- •Customizing Table Cells
- •Copying Tables to the Clipboard
- •Saving Tables to a File
- •Table Commands
- •Text Objects
- •Part III. Basic Single Equation Analysis
- •Chapter 15. Basic Regression
- •Equation Objects
- •Specifying an Equation in EViews
- •Estimating an Equation in EViews
- •Equation Output
- •Working with Equations
- •Estimation Problems
- •Chapter 16. Additional Regression Methods
- •Special Equation Terms
- •Weighted Least Squares
- •Heteroskedasticity and Autocorrelation Consistent Covariances
- •Two-stage Least Squares
- •Nonlinear Least Squares
- •Generalized Method of Moments (GMM)
- •Chapter 17. Time Series Regression
- •Serial Correlation Theory
- •Testing for Serial Correlation
- •Estimating AR Models
- •ARIMA Theory
- •Estimating ARIMA Models
- •ARMA Equation Diagnostics
- •Nonstationary Time Series
- •Unit Root Tests
- •Panel Unit Root Tests
- •Chapter 18. Forecasting from an Equation
- •Forecasting from Equations in EViews
- •An Illustration
- •Forecast Basics
- •Forecasting with ARMA Errors
- •Forecasting from Equations with Expressions
- •Forecasting with Expression and PDL Specifications
- •Chapter 19. Specification and Diagnostic Tests
- •Background
- •Coefficient Tests
- •Residual Tests
- •Specification and Stability Tests
- •Applications
- •Part IV. Advanced Single Equation Analysis
- •Chapter 20. ARCH and GARCH Estimation
- •Basic ARCH Specifications
- •Estimating ARCH Models in EViews
- •Working with ARCH Models
- •Additional ARCH Models
- •Examples
- •Binary Dependent Variable Models
- •Estimating Binary Models in EViews
- •Procedures for Binary Equations
- •Ordered Dependent Variable Models
- •Estimating Ordered Models in EViews
- •Views of Ordered Equations
- •Procedures for Ordered Equations
- •Censored Regression Models
- •Estimating Censored Models in EViews
- •Procedures for Censored Equations
- •Truncated Regression Models
- •Procedures for Truncated Equations
- •Count Models
- •Views of Count Models
- •Procedures for Count Models
- •Demonstrations
- •Technical Notes
- •Chapter 22. The Log Likelihood (LogL) Object
- •Overview
- •Specification
- •Estimation
- •LogL Views
- •LogL Procs
- •Troubleshooting
- •Limitations
- •Examples
- •Part V. Multiple Equation Analysis
- •Chapter 23. System Estimation
- •Background
- •System Estimation Methods
- •How to Create and Specify a System
- •Working With Systems
- •Technical Discussion
- •Vector Autoregressions (VARs)
- •Estimating a VAR in EViews
- •VAR Estimation Output
- •Views and Procs of a VAR
- •Structural (Identified) VARs
- •Cointegration Test
- •Vector Error Correction (VEC) Models
- •A Note on Version Compatibility
- •Chapter 25. State Space Models and the Kalman Filter
- •Background
- •Specifying a State Space Model in EViews
- •Working with the State Space
- •Converting from Version 3 Sspace
- •Technical Discussion
- •Chapter 26. Models
- •Overview
- •An Example Model
- •Building a Model
- •Working with the Model Structure
- •Specifying Scenarios
- •Using Add Factors
- •Solving the Model
- •Working with the Model Data
- •Part VI. Panel and Pooled Data
- •Chapter 27. Pooled Time Series, Cross-Section Data
- •The Pool Workfile
- •The Pool Object
- •Pooled Data
- •Setting up a Pool Workfile
- •Working with Pooled Data
- •Pooled Estimation
- •Chapter 28. Working with Panel Data
- •Structuring a Panel Workfile
- •Panel Workfile Display
- •Panel Workfile Information
- •Working with Panel Data
- •Basic Panel Analysis
- •Chapter 29. Panel Estimation
- •Estimating a Panel Equation
- •Panel Estimation Examples
- •Panel Equation Testing
- •Estimation Background
- •Appendix A. Global Options
- •The Options Menu
- •Print Setup
- •Appendix B. Wildcards
- •Wildcard Expressions
- •Using Wildcard Expressions
- •Source and Destination Patterns
- •Resolving Ambiguities
- •Wildcard versus Pool Identifier
- •Appendix C. Estimation and Solution Options
- •Setting Estimation Options
- •Optimization Algorithms
- •Nonlinear Equation Solution Methods
- •Appendix D. Gradients and Derivatives
- •Gradients
- •Derivatives
- •Appendix E. Information Criteria
- •Definitions
- •Using Information Criteria as a Guide to Model Selection
- •References
- •Index
- •Symbols
- •.DB? files 266
- •.EDB file 262
- •.RTF file 437
- •.WF1 file 62
- •@obsnum
- •Panel
- •@unmaptxt 174
- •~, in backup file name 62, 939
- •Numerics
- •3sls (three-stage least squares) 697, 716
- •Abort key 21
- •ARIMA models 501
- •ASCII
- •file export 115
- •ASCII file
- •See also Unit root tests.
- •Auto-search
- •Auto-series
- •in groups 144
- •Auto-updating series
- •and databases 152
- •Backcast
- •Berndt-Hall-Hall-Hausman (BHHH). See Optimization algorithms.
- •Bias proportion 554
- •fitted index 634
- •Binning option
- •classifications 313, 382
- •Boxplots 409
- •By-group statistics 312, 886, 893
- •coef vector 444
- •Causality
- •Granger's test 389
- •scale factor 649
- •Census X11
- •Census X12 337
- •Chi-square
- •Cholesky factor
- •Classification table
- •Close
- •Coef (coefficient vector)
- •default 444
- •Coefficient
- •Comparison operators
- •Conditional standard deviation
- •graph 610
- •Confidence interval
- •Constant
- •Copy
- •data cut-and-paste 107
- •table to clipboard 437
- •Covariance matrix
- •HAC (Newey-West) 473
- •heteroskedasticity consistent of estimated coefficients 472
- •Create
- •Cross-equation
- •Tukey option 393
- •CUSUM
- •sum of recursive residuals test 589
- •sum of recursive squared residuals test 590
- •Data
- •Database
- •link options 303
- •using auto-updating series with 152
- •Dates
- •Default
- •database 24, 266
- •set directory 71
- •Dependent variable
- •Description
- •Descriptive statistics
- •by group 312
- •group 379
- •individual samples (group) 379
- •Display format
- •Display name
- •Distribution
- •Dummy variables
- •for regression 452
- •lagged dependent variable 495
- •Dynamic forecasting 556
- •Edit
- •See also Unit root tests.
- •Equation
- •create 443
- •store 458
- •Estimation
- •EViews
- •Excel file
- •Excel files
- •Expectation-prediction table
- •Expected dependent variable
- •double 352
- •Export data 114
- •Extreme value
- •binary model 624
- •Fetch
- •File
- •save table to 438
- •Files
- •Fitted index
- •Fitted values
- •Font options
- •Fonts
- •Forecast
- •evaluation 553
- •Foreign data
- •Formula
- •forecast 561
- •Freq
- •DRI database 303
- •F-test
- •for variance equality 321
- •Full information maximum likelihood 698
- •GARCH 601
- •ARCH-M model 603
- •variance factor 668
- •system 716
- •Goodness-of-fit
- •Gradients 963
- •Graph
- •remove elements 423
- •Groups
- •display format 94
- •Groupwise heteroskedasticity 380
- •Help
- •Heteroskedasticity and autocorrelation consistent covariance (HAC) 473
- •History
- •Holt-Winters
- •Hypothesis tests
- •F-test 321
- •Identification
- •Identity
- •Import
- •Import data
- •See also VAR.
- •Index
- •Insert
- •Instruments 474
- •Iteration
- •Iteration option 953
- •in nonlinear least squares 483
- •J-statistic 491
- •J-test 596
- •Kernel
- •bivariate fit 405
- •choice in HAC weighting 704, 718
- •Kernel function
- •Keyboard
- •Kwiatkowski, Phillips, Schmidt, and Shin test 525
- •Label 82
- •Last_update
- •Last_write
- •Latent variable
- •Lead
- •make covariance matrix 643
- •List
- •LM test
- •ARCH 582
- •for binary models 622
- •LOWESS. See also LOESS
- •in ARIMA models 501
- •Mean absolute error 553
- •Metafile
- •Micro TSP
- •recoding 137
- •Models
- •add factors 777, 802
- •solving 804
- •Mouse 18
- •Multicollinearity 460
- •Name
- •Newey-West
- •Nonlinear coefficient restriction
- •Wald test 575
- •weighted two stage 486
- •Normal distribution
- •Numbers
- •chi-square tests 383
- •Object 73
- •Open
- •Option setting
- •Option settings
- •Or operator 98, 133
- •Ordinary residual
- •Panel
- •irregular 214
- •unit root tests 530
- •Paste 83
- •PcGive data 293
- •Polynomial distributed lag
- •Pool
- •Pool (object)
- •PostScript
- •Prediction table
- •Principal components 385
- •Program
- •p-value 569
- •for coefficient t-statistic 450
- •Quiet mode 939
- •RATS data
- •Read 832
- •CUSUM 589
- •Regression
- •Relational operators
- •Remarks
- •database 287
- •Residuals
- •Resize
- •Results
- •RichText Format
- •Robust standard errors
- •Robustness iterations
- •for regression 451
- •with AR specification 500
- •workfile 95
- •Save
- •Seasonal
- •Seasonal graphs 310
- •Select
- •single item 20
- •Serial correlation
- •theory 493
- •Series
- •Smoothing
- •Solve
- •Source
- •Specification test
- •Spreadsheet
- •Standard error
- •Standard error
- •binary models 634
- •Start
- •Starting values
- •Summary statistics
- •for regression variables 451
- •System
- •Table 429
- •font 434
- •Tabulation
- •Template 424
- •Tests. See also Hypothesis tests, Specification test and Goodness of fit.
- •Text file
- •open as workfile 54
- •Type
- •field in database query 282
- •Units
- •Update
- •Valmap
- •find label for value 173
- •find numeric value for label 174
- •Value maps 163
- •estimating 749
- •View
- •Wald test 572
- •nonlinear restriction 575
- •Watson test 323
- •Weighting matrix
- •heteroskedasticity and autocorrelation consistent (HAC) 718
- •kernel options 718
- •White
- •Window
- •Workfile
- •storage defaults 940
- •Write 844
- •XY line
- •Yates' continuity correction 321

488—Chapter 16. Additional Regression Methods
setting your convergence criterion too low, which can occur if your nonlinear specification is particularly complex.
If you wish to change the convergence criterion, enter the new value in the Options tab. Be aware that increasing this value increases the possibility that you will stop at a local minimum, and may hide misspecification or non-identification of your model.
See “Setting Estimation Options” on page 951, for related discussion.
Generalized Method of Moments (GMM)
The starting point of GMM estimation is a theoretical relation that the parameters should satisfy. The idea is to choose the parameter estimates so that the theoretical relation is satisfied as “closely” as possible. The theoretical relation is replaced by its sample counterpart and the estimates are chosen to minimize the weighted distance between the theoretical and actual values. GMM is a robust estimator in that, unlike maximum likelihood estimation, it does not require information of the exact distribution of the disturbances. In fact, many common estimators in econometrics can be considered as special cases of GMM.
The theoretical relation that the parameters should satisfy are usually orthogonality condi-
tions between some (possibly nonlinear) function of the parameters f( θ) |
and a set of |
instrumental variables zt : |
|
E( f( θ) ′Z ) = 0 , |
(16.46) |
where θ are the parameters to be estimated. The GMM estimator selects parameter estimates so that the sample correlations between the instruments and the function f are as close to zero as possible, as defined by the criterion function:
J( θ) = ( m( θ) ) ′Am( θ) , |
(16.47) |
where m( θ) = f( θ) ′ Z and A is a weighting matrix. Any symmetric positive definite matrix A will yield a consistent estimate of q . However, it can be shown that a necessary (but not sufficient) condition to obtain an (asymptotically) efficient estimate of q is to set A equal to the inverse of the covariance matrix of the sample moments m . It is worth noting here that in standard single equation GMM, EViews estimates a model with the objective function (16.47) divided by the number of observations. For equations with panel data (“GMM Estimation” beginning on page 905) the objective function is not similarly scaled.
Many standard estimators, including all of the system estimators provided in EViews, can be set up as special cases of GMM. For example, the ordinary least squares estimator can be viewed as a GMM estimator, based upon the conditions that each of the right-hand variables is uncorrelated with the residual.
Generalized Method of Moments (GMM)—489
Estimation by GMM in EViews
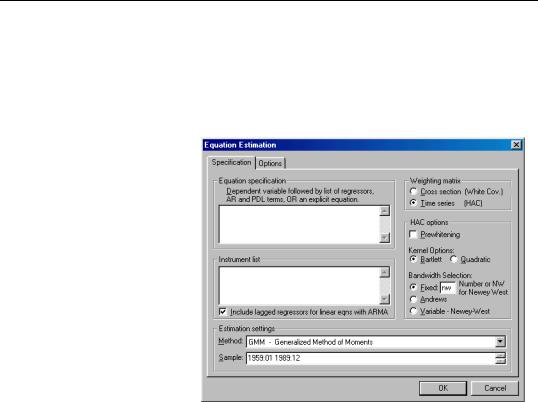
To estimate an equation by GMM, either create a new equation object by selecting Object/ New Object.../Equation, or press the Estimate button in the toolbar of an existing equation. From the Equation Specification dialog choose Estimation Method: GMM. The estimation specification dialog will change as depicted below.
To obtain GMM estimates in EViews, you need to write the moment condition as an orthogonality condition between an expression including the parameters and a set of instrumental variables. There are two ways you can write the orthogonality condition: with and without a dependent variable.
If you specify the equation either by listing variable names or by an expression with an equal
sign, EViews will interpret the moment condition as an orthogonality condition between the instruments and the residuals defined by the equation. If you specify the equation by an expression without an equal sign, EViews will orthogonalize that expression to the set of instruments.
You must also list the names of the instruments in the Instrument list field box of the Equation Specification dialog box. For the GMM estimator to be identified, there must be at least as many instrumental variables as there are parameters to estimate. EViews will always include the constant in the list of instruments.
For example, if you type, |
|
|
|
Equation Specification: y |
c |
x |
|
Instrument list: |
c |
z |
w |
the orthogonality conditions given by:

490—Chapter 16. Additional Regression Methods
|
Σ( yt − c( 1 ) − c( 2) xt) = 0 |
|
|
|
Σ( yt − c( 1) − c( 2 )xt) zt |
= 0 |
(16.48) |
|
Σ ( yt − c( 1 ) − c( 2 ) xt)wt = 0 |
|
|
If you enter the specification, |
|
|
|
Equation Specification: c(1)*log(y)+x^c(2) |
|
|
|
Instrument list: |
c z z(-1) |
|
|
the orthogonality conditions are: |
|
|
|
|
Σ( c( 1 )log yt + xtc(2)) |
= 0 |
|
|
c(2) |
|
(16.49) |
|
Σ( c( 1 )log yt + xt )zt |
= 0 |
|
|
|
||
|
Σ( c( 1) log yt + xtc(2) )zt − 1 |
= 0 |
|
On the right part of the Equation Specification dialog are the options for selecting the weighting matrix A in the objective function. If you select Weighting Matrix: Cross section (White Cov), the GMM estimates will be robust to heteroskedasticity of unknown form.
If you select Weighting Matrix: Time series (HAC), the GMM estimates will be robust to heteroskedasticity and autocorrelation of unknown form. For the HAC option, you have to specify the kernel type and bandwidth.
•The Kernel Options determine the functional form of the kernel used to weight the autocovariances in computing the weighting matrix.
•The Bandwidth Selection option determines how the weights given by the kernel change with the lags of the autocovariances in the computation of the weighting matrix. If you select Fixed bandwidth, you may either enter a number for the bandwidth or type nw to use Newey and West’s fixed bandwidth selection criterion.
•The Prewhitening option runs a preliminary VAR(1) prior to estimation to “soak up” the correlation in the moment conditions.
The technical notes in “Generalized Method of Moments (GMM)” on page 716 describe these options in greater detail.
Example
Tauchen (1986) considers the problem of estimating the taste parameters β , γ from the Euler equation:
( βRt + 1wt−γ+ 1 − 1 ) ′zt = 0 |
(16.50) |

Generalized Method of Moments (GMM)—491
where we use instruments zt = ( 1, wt, wt − 1, rt, rt − 1) ′ . To estimate the parameters β , γ by GMM, fill in the Equation Specification dialog as:
Equation Specification: c(1)*r(+1)*w(+1)^(-c(2))-1
Instrument list: c w w(-1) r r(-1)
The estimation result using the default HAC Weighting Matrix option looks as follows:
Dependent Variable: Implicit Equation
Method: Generalized Method of Moments
Date: 09/26/97 Time: 14:02
Sample(adjusted): 1891 1982
Included observations: 92 after adjusting endpoints
No prewhitening
Bandwidth: Fixed (3)
Kernel: Bartlett
Convergence achieved after: 7 weight matricies, 7 total coef iterations
C(1)*R(+1)*W(+1)^(-C(2))-1
Instrument list: C W W(-1) R R(-1)
|
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
C(1) |
0.934096 |
0.018751 |
49.81600 |
0.0000 |
C(2) |
1.366396 |
0.741802 |
1.841995 |
0.0688 |
|
|
|
|
|
S.E. of regression |
0.154084 |
Sum squared resid |
2.136760 |
|
Durbin-Watson stat |
1.903837 |
J-statistic |
|
0.054523 |
|
|
|
|
|
Note that when you specify an equation without a dependent variable, EViews does not report some of the regression statistics such as the R-squared. The J-statistic reported at the bottom of the table is the minimized value of the objective function, where we report (16.47) divided by the number of observations (see “Generalized Method of Moments (GMM)” beginning on page 488 for additional discussion). This J-statistic may be used to carry out hypothesis tests from GMM estimation; see Newey and West (1987a). A simple application of the J-statistic is to test the validity of overidentifying restrictions when you have more instruments than parameters to estimate. In this example, we have five instruments to estimate two parameters and so there are three overidentifying restrictions. Under the null hypothesis that the overidentifying restrictions are satisfied, the J-statistic times the number of regression observations is asymptotically χ2 with degrees of freedom equal to the number of overidentifying restrictions. You can compute the test statistic as a named scalar in EViews using the commands:
scalar overid=eq_gmm.@regobs*eq_gmm.@jstat
scalar overid_p=1-@cchisq(overid,3)
where EQ_GMM is the name of the equation containing the GMM estimates. The second command computes the p-value of the test statistic as a named scalar OVERID_P. To view the value of OVERID_P, double click on its name; the value will be displayed in the status line at the bottom of the EViews window.

492—Chapter 16. Additional Regression Methods
