Позначення констант рівноваг

Реакції (загальний вигляд та приклади)	Позначення	Примітки
1. Константи стійкості комплексів
m M + n L  MmLn	nm	Загальні константи стійкості
2 Ag+ + 6 I‑  Ag2I64‑	62
M + n L  MLn	n	Для одноядерних комплексів m = 1 опускають
Ag+ + NH3  AgNH3+	1
Ag+ + 2 NH3  Ag(NH3)2+	2
MLn‑1 + L  MLn	Kn	K – ступінчаті константи стійкості, Kn = n / n‑1
Ag+ + NH3  AgNH3+	K1
AgNH3+ + NH3  Ag(NH3)2+	K2
2O  H+ + OH‑	Kw	Іонний добуток води
m H+ + L  HmL	Hm	Якщо L – ліганд, H+ комплексоутворювач, то Hm – це 1m
H+ + PO43‑  HPO42‑	H1
2 H+ + PO43‑  H2PO4‑	H2
3 H+ + PO43‑  H3PO4	H3
H+ + Hm‑1L  HmL	KHm	KHm – ступінчаті константи стійкості KHm = Hm / H(m‑1)
H+ + PO43‑  HPO42‑	KH1
H+ + HPO42‑  H2PO4‑	KH2
H+ + H2PO4‑  H3PO4	KH3
Hm+1L  HmL + H+	Ka(N‑m)	Ступінчата константа іонізації кислоти HNL, Ka(N‑m) = 1 / KH(m+1)
H3PO4  H+ + H2PO4‑	Ka1
H2PO4‑  H+ + HPO42‑	Ka2
HPO42‑  H+ + PO43‑	Ka3

m M + n OH‑  Mm(OH)n	nm	Константи стійкості гідроксокомплексів (окремого випадку комплексів)
2 Fe3+ + 2 OH‑  Fe2(OH)24+	22
Hg2+ + OH‑  HgOH+	1
Hg2+ + 2 OH‑  Hg(OH)2	2
Hg2+ + 3 OH‑  Hg(OH)3‑	3

2. Константи кислотно-основних рівноваг (продовження)

m M + n H2O  Mm(OH)n + n H+	*nm	Константа взаємодії іона металу з H2O *nm = nm Kwn, m = 1 опускають
2 Fe3+ + 2 H2O  Fe2(OH)24+ + 2 H+	*22
M + n H2O  M(OH)n + n H+	*n
Hg2+ + H2O  HgOH+ + H+	*1
Hg2+ + 2 H2O  Hg(OH)2 + 2 H+	*2
Hg2+ + 3 H2O  Hg(OH)3‑ + 3 H+	*3
3. Константи гетерогенних реакцій
L  L(орг), або L  ,	KD	Константа розподілу (в дужках – розчинник)
Br2  Br2(CCl4), або Br2 
Al3+ + 3 HOxin (орг)   AlOxin3 (орг)+ 3 H+	Kex	Загальна константа екстракції
L(g)  L	Kp	Закон Генрі, p в атмосферах
CO2(g)  CO2
L(s)  L, L(l)  L,	Ks	Розчинність (s – тверда, l – рідка речовина)
I2(s)  I2, Br2(l)  Br2,
MmLn(s)  mMLq + (n – m q) L	Ksq	Добуток розчинності (q = 0 можна опускати), Ksq = Ks0 q. Нижче – складний випадок, де слідом за Ks у дужках наведено продукти у розчині.
HgI2(s)  Hg2+ + 2 I‑	Ks0
HgI2(s)  HgI+ + I‑	Ks1
HgI2(s)  HgI2	Ks2
HgI2(s) + I‑  HgI3‑	Ks3
HgI2(s) + 2 I‑  HgI42‑	Ks4

Концентраційні константи. Константу рівноваги, виражену через рівноважні концентрації (3) називають концентраційною. Підставляючи вираз (6) у ЗДМ (3), приходимо до його аналога із рівноважними концентраціями замість активностей,

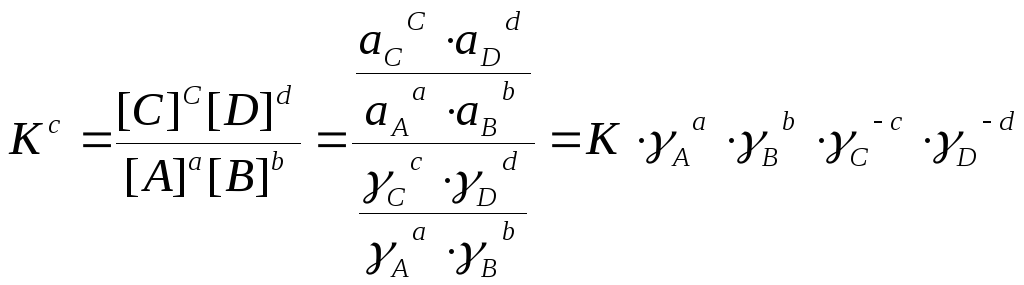
Або дотримуючись алгебраїчного підходу в записі реакцій і рівнянь, маємо:

= K^c = K · ()^-1,

lg K^c = lg K -lg () = lgK – _j lg _j. (15)

Концентраційна константа рівноваги K^c залежить від складу розчину через _j. Часто користуючись K^c, не вказуватимемо індекс «c». У довідниках наводять як термодинамічні (при І = 0), так і концентраційні константи.

Приблизно оцінюючи іонну силу, обмежуємось внеском від переважаючих компонентів, зокрема іонів сильних електролітів (тих, що дисоційовані повністю). Досліджуючи константи, з сильних електролітів утворюють так званий «сольовий фон», що стабілізує коефіцієнти активності. У водяних розчинах сильними є кислоти HCl, HClO₄, HBr, HI, H₂SO₄ (за першим ступенем дисоціації), HNO₃; основи та солі з катіонами Na⁺, K⁺, Rb⁺, Cs⁺ , не схильними до комплексоутворення, і солі з аніоном ClO₄^‑.

Рівноважні концентрації розраховують за концентраційними константами, вдаючись до ітерацій (послідовних наближень). Розрахувавши [A_j] за lg K^c, що відповідають наближеній іонній силі, уточнюють І та lg K^c, й знову [A_j]. Процес закінчують, якщо значення lg K^c відрізняються від попередніх у межах похибок. Ітерації сходяться, бо lg K^c повільно змінюються з [A_j].

Наприклад, для реакції

Ca₅(OH)(PO₄)₃(s)  5 Ca²⁺ + OH^- + 3 PO₄^3-, lg K_s = ‑55,91 [I=0],

lg K_s^c у середовищі c(NaClO₄) = 0,1 моль/л обчислюємо так. Електроліт NaClO₄ – сильний,

[Na⁺] = [ClO₄^‑] = c(NaClO₄) = 0,1 моль/л.

Без внеску від продуктів реакції іонна сила

I = {[Na⁺] + [ClO₄^‑]} / 2 = 0,1.

За формулою Девіса,

lg  = ‑ 0,5 / (1 +) + 0,15I = -0,105.

Підставляючи її у вираз (6), маємо

lg K_s^с = lg K_s ‑ {_j z_j²} lg  = ‑55,91 ‑ {5·2² +

+ 1·(‑1)² + 3·(‑3)²}·(-0,105) = ‑55,91 + 30·0,105 = -52,76. 

Лінійні комбінації реакцій

Ми вже мали змогу звернути увагу, що рівняння приєднання кількох протонів до багатозарядного аніону (або кількох лігандів до іону-комплексоутворювача) характеризуються загальною константою, яка дорівнює добутку ступінчастих констант: β_n = K·K·…·K_n.

Аналогічним чином можна обчислитити константу більш складної рівноваги, використовючи константи простих рівноваг.

Приклад 1. Розглянемо рівновагу розчинення малорозчинної солі слабої кислоти в розчині сильної кислоти.

CaCO₃↓ + 2H⁺  Ca²⁺ + H₂O + CO₂; K-?

Розв’язання. Реакція складається з двох простих рівноваг:

CaCO₃↓ Ca²⁺ +CO₃^2- ; K_s=10^‑8,52

CO₃^2- +2H⁺H₂O+CO₂; β_H2=K_H1·K_H2=10^10,33· 10^6,35=10^16,68

Значить константа рівноваги вихідної реакції:             K= K_s β_H2=10^‑8,52 ·10^16,68=10^8,16;

Відповідь: K=1,45·10⁸.

Приклад 2. Рівновага розчинення малорозчинного гідроксиду в розчині аміаку:

Cu(OH)₂↓ +4NH₃ Cu(NH₃)₄²⁺+2OH^- K=?

Розв’язання. Вихідною речовиною є осад гидроксиду, значить першою рівновагою слід розглянути рівновагу розчинення:

Cu(OH)₂↓ Cu²⁺+2OH K_s = 10^-19,32.

Утворені іони Cu²⁺ взаємодіють із молекулами аміаку:

Cu²⁺ + 4NH₃  Cu(NH₃)₄²⁺ β₄ =10^11,75.

константа рівнваги вихідної реакції:                                 K = K_s·β₄=10^-19,32·10^11,75 = 10^-7,57.

Відповідь: K = 2,69·10^-8.

Приклад 3. Рівновага утворення осаду при руйнуванні комплексної сполуки

BiI₄^-+PO₄^3-  BiPO₄↓ + 4I^-.

Розв’язання. Вихідними є комплексні аніони, значить першою рівновагою слід розглянути рівновагу дисоціації:

BiI₄^-  Bі³⁺ + 4I^- β₄^-1 = 10^-15.

Утворені іони Bі³⁺ взаємодіють із аніонами фосфату

Bі³⁺ + PO₄^3-  BiPO₄↓ K_s^-1 = 10²².

константа рівноваги вихідної реакції:                                 K= β₄^-1· K_s^-1 =10^-15·10^22,9 = 10^7,9;

Відповідь: K = 7,94·10⁷.

Теоретично вивчаючи рівноважні системи, враховуємо ЗДМ для різних реакцій. Замість того, щоб перетворювати алгебраїчні рівняння ЗДМ, наочніше перетворити реакції, для яких є довідкові дані, переходячи до лінійних комбінацій реакцій.

Розглянемо вихідні реакції

   _ij A_j 16

де i – номер реакції, _ij – стехіометричний коефіцієнт у i-й реакції при реагенті A_j . Множачи реакції на множники k_i й додаючи добутки, утворюємо лінійну комбінацію

    k_i _ij) A_j 17

із стехіометричними коефіцієнтами – лінійними комбінаціями коефіцієнтів вихідних реакцій.

Логарифмуючи рівняння ЗДМ для реакції (7), маємо

 _ij lg a_j = lg K_i,

де K_і – константа ЗДМ для і-ї реакції; a_j – активність реагенту A_j. Створюючи лінійну комбінацію цих рівнянь, маємо

 k_i _ij) lg a_j =  lg K_i = lg K, (18)

де K – константа ЗДМ лінійної комбінації (тобто реакції 8). Не ускладнюючи рівнянь ЗДМ, k_i вибираємо так, щоб коефіцієнти  k_i _ij) при деяких реагентах обертались на 0 (реагенти «скорочувались»), і відповідна активність у ЗДМ не входила. Комбінуючи n реакцій, «скорочуємо» принаймні (n - 1) реагентів. Лінійна комбінація задовольняє вимозі, що число атомів кожного елемента у реакції зберігається, бо їй задовольняють вихідні реакції.

Лінійно незалежні реакції – такі, що жодна з них не є лінійною комбінацією інших. Математичні терміни «лінійна комбінація» та «лінійна незалежність» відповідають структурі множини реагентів та реакцій. ЗДМ для незалежних реакцій є незалежними алгебраїчними рівняннями. Залежним реакціям відповідають залежні рівняння ЗДМ.

Розглянемо найчастіше вживані лінійні комбінації. Найпростіша з них – зворотна реакція, комбінація з однієї реакції, із множником (‑1). Наприклад, для щавлевої (оксалатної) кислоти маємо

H⁺ + C₂O₄^2‑  HC₂O₄^‑,  lg K_H1 = 4,266,

H⁺ + HC₂O₄^‑  H₂C₂O₄,  lg K_H2 = 1,252.