6. Концентраційно-логарифмічні діаграм (клд)

КЛД для гетерогенних систем. ЗДМ – одночленний алгебраїчний вираз, із різними показниками ступеня при рівноважних концентраціях. Форма графіків залежності між концентраціями різна, й їх незручно будувати як допоміжний засіб теоретичних досліджень. Але логарифми рівноважних концентрацій залежать один від одного лінійно, й їх графіки легко будувати й сприймати. У логарифмічних координат є ще одна перевага: за ними можна вивчати як великі, так і малі рівноважні концентрації – а рівноважні концентрації продуктів змінюються на багато порядків!

Концентраційно-логарифмічні діаграми (КЛД) – це сукупність графіків логарифмів рівноважних концентрацій продуктів реакцій як функцій так званої «головної змінної», показника для одного з реагентів, pX = ‑ lg [X]. Здебільшого, X – або іон водню H⁺ (тоді pX= = pH), або ліганд L у комплексах, або електрон e^- у відновленні,

pe = E / k,

де k – множник Нернста. Часто потрібен лише ескіз КЛД, без деталей, де обмежуються частинами графіків для найбільших концентрацій продуктів реакцій та самої [X]. Їх зручно будувати і сприймати зверху вниз та справа наліво – так, як ми пишемо тексти. Саме таким умовам відповідають згадані координати КЛД, вироблені скандинавською педагогічною школою.

У рівняннях ЗДМ для гетерогенних систем звичайно 2 змінних – незалежна («головна») і залежна (логарифм концентрації продукту), і графік – пряма лінія.

Розглянемо приклад – КЛД (головна змінна pCl) для комплексів у насиченому розчині AgCl(s). Логарифми констант – для 20 ^оС та I = 4:

AgCl (s)  Ag⁺ + Cl^‑,   lg K_s0 = ‑10,40, Ag⁺ + n Cl^‑  AgCl_n^1‑n, lg _n = 3,45 (n = 1), 5,57 (n = 2), 6,0 (n = 3).

Крок 1. Складімо лінійні комбінації реакцій так, щоб у них із твердої фази, AgCl (s), та пов’язаних із головною змінною іоном Cl^‑, утворювався один певний продукт, та розрахуємо

lg K_sn = lg K_s0 + lg _n .

Здобуваємо:

AgCl (s) – Cl^-  Ag⁺,    lg K_s0 = -10,40,

AgCl (s)  AgCl,    lg K_s1 = -6,95,

AgCl (s)  Cl^‑  AgCl₂^-,    lg K_s2 = -4,73,

AgCl (s) + 2 Cl^-  AgCl₃^2-,    lg K_s3 = -4,40.

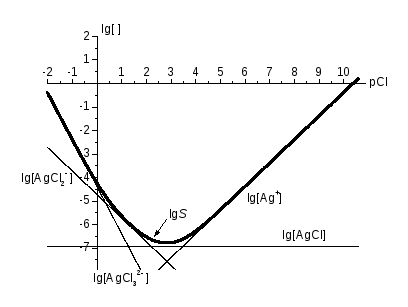
Рис. 1. КЛД для системи AgCl (s) – рCl.

Крок 2. За рівняннями ЗДМ (у логарифмічній формі) для цих реакцій,

lg [AgCl_і^1‑і] = lg K _sі + (1 – і) pCl,

будуємо прямі (рис. 1). Рівняння для них можна і не записувати. Достатньо уявляти, що прямі перетинають вісь ординат у точках lg K _sn та йдуть із тангенсами кутів нахилу, що дорівнюють (із точністю до знака) коефіцієнтові при Cl^‑ у наведених вище реакціях. Оскільки AgCl (s) незаряджений, а у Cl^‑ заряд дорівнює (‑1), то відповідний тангенс дорівнює зарядові продукту реакції. Напрям нахилу легко збагнути через хімічні уявлення. Так, із зростом рCl зменшується [Cl^‑], і, через зсув відповідних рівноваг, зростає [Ag⁺] та lg [Ag⁺], не змінюється [AgCl] та зменшуються рівноважні концентрації аніонних комплексів.

Будуючи пряму, обчислімо координати двох її точок. Одну з них, на осі ординат, уже маємо. Другу виберемо далеко від першої, зменшуючи похибки відтворення графіка за лінійкою. Для lg [Ag⁺] другу точку виберемо на осі абсцис. Тангенс дорівнює 1, й зріст абсциси й ординати однаковий. Отже, графік проводимо через точки (0; ‑ 10,40) та (10,40; 0). Для lg [AgCl₃^2‑] тангенс дорівнює (‑2), і його можна провести через точки (0; ‑ 4,40) та (‑ 4,40 / 2 = ‑ 2,2; 0). Інші графіки будуємо аналогічно. Абсциси pCl їх точок перетину дорівнюють логарифмам ступінчатих констант стійкості.

Розглянемо ще КЛД (головна змінна pH) для насиченого розчину Al(OH)₃(s), де: lg K_s0(Al(OH)₃, аморфн.) = -32,34; у комплексів Al³⁺ із OH^-: lg ₁ = 9,03, lg ₂ = 18,69, lg ₃ = 25,99, lg ₄ = 32,99, lg ₂₂ = 20,30, lg ₄₃ = 42,05, lg K_w = -14,00.

Крок 1. Складемо лінійні комбінації реакцій:

Al(OH)₃ (s) + 3 H⁺ – 3 H₂O    Al³⁺,     lg *K_s0 = 9,66,

Al(OH)₃ (s) + 2 H⁺ – 2 H₂O  AlOH²⁺,     lg *K_s1 = 4,69,

Al(OH)₃ (s) + H⁺ – H₂O  Al(OH)₂⁺,     lg *K_s2 = 0,35,

Al(OH)₃ (s)  Al(OH)₃,     lg *K_s3 = -5,35,

Al(OH)₃ (s) – H⁺ + H₂O  Al(OH)₄^‑,     lg *K_s4 = -13,35,

2 Al(OH)₃ (s) + 4 H⁺ – 4 H₂O  Al₂(OH)₂⁴⁺,  lg *K_s22 = 11,64,

3 Al(OH)₃ (s) + 5 H⁺ – 8 H₂O  Al₃(OH)₄⁵⁺, lg *K_s43 = 15,03.

Логарифми констант лінійних комбінацій пов’язані з довідковими даними співвідношенням

lg *K_sji = i lg K_s0 + lg  _ji + (j –3 i) lg K_w

(перевірте його!!).

Крок 2. Будуємо прямі (рис. 2)

lg [Al_i(OH)_j^3 i‑j] = lg *K_sji + (j – 3 i) pH.

Як і у попередньому прикладі, рівняння для них майже очевидні: прямі перетинають вісь ординат у точках lg *K_sji та йдуть із тангенсами кутів нахилу, що дорівнюють зарядові продукту реакції. Напрям нахилу легко збагнути через хімічні уявлення. Так, зі зростанням рН зменшується [Н⁺], і, через зсув відповідних рівноваг, зменшується [Al³⁺], lg [Al³⁺] та відповідні величини для катіонних комплексів, не змінюється [Al(ОН)₃], зростають рівноважні концентрації аніонних комплексів. Подібні уявлення важливі для самоконтролю при побудові КЛД у вправах.

Не радимо відкладати на осі ординат великі lg *K_sji , бо такі концентрації нездійсненні (хто може зробити розчин із [AlОН²⁺] = *K_sji = 10^4,69 моль/л ?!), і КЛД невиправдано витягнеться вгору. Краще вибрати інші точки, наприклад, перетину з віссю абсцис. Оскільки тангенс кута нахилу тут дорівнює (‑2), зарядові іону зі зворотним знаком, то спуск від точки (0; 4,69) до осі абсцис приведе до зміни абсциси на 4,69 / 2  2,3 (оцінка наближена, бо точніше на графіку не відкладеш!), і координати точки (2,3; 0). Як другу можна узяти відносно далеку точку, з абсцисою 10. Різниця абсцис двох точок дорівнює 10 – 2,3 = 7,7, а різниця ординат удвічі більша, тобто 2  7,7 = 15,4. Координати другої точки (10; ‑15,4). Аналогічно будуємо інші графіки.

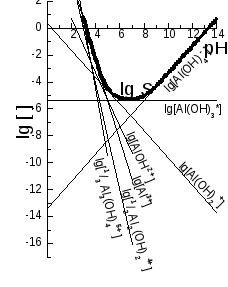
Рис. 2. КЛД для системи Al(OH)₃ (s) – рH.

Алгоритм побудови КЛД. Узагальнюючи операції, що розглянуті у прикладах, сформулюємо алгоритм:

1. Лінійними комбінаціями привести реакції до

(i / m) M_iL_j (s або g) + (j - i n / m) L  M_iL_j,  lg K_sji, (17)

й обчислити lg K_sji. У реакції можна включати і розчинник H₂O, концентрація якого не входить у ЗДМ.

2. Побудувати прямі

lg [M_iL_j] = lg K_sji – (j – i n / m) pL, (18a)

або

lg [M_iL_j] = lg K_sji – (j – i n / m) pL + (i / m) lg p(M_iL_j (g)), (18б)

де p(M_iL_j (g)) – заданий парціальний тиск газової фази. Прямі відсікають на осі ординат відрізки lg K_sji, із нахилом до осі абсцис під кутом, тангенс якого дорівнює (j - i n / m).

Радимо не наслідувати алгоритм наосліп, ще й намагаючись знайти відповідність між формулами (17) та (18) із загальними індексами та формулами сполук у Вашій конкретній системі. Краще зрозуміти його операції і будувати відповідні лінійні комбінації реакцій для Вашої системи.

Графіки логарифмів розчинності. Розчинність – це концентрація речовини, що перейшла у насичений розчин. Розглянемо реакції у першому прикладі – скільки формульних одиниць AgCl(s) витрачається на одну частинку різних продуктів у розчині. Термін «формульна одиниця» вживають замість «частинка», бо частинки AgCl(s) окремо від твердої фази не існує. Тут по одній формульній одиниці AgCl(s) витрачається у реакціях на одну частинку як Ag⁺, так і AgCl (у розчині!), AgCl₂^- та AgCl₃^2-. Розчинність складається з усіх внесків,

S(AgCl) = [Ag⁺] + [AgCl] + [AgCl₂^-] + [AgCl₃^2-] =  [AgCl_j^1-j].

Логарифм суми приблизно дорівнює логарифмові найбільшого доданка.

Для прикладу з багатоядерними комплексами розчинність – це

S(Al(OH)₃) =[Al³⁺] + [AlOH²⁺] + [Al(OH)₂⁺] + [Al(OH)₃] + [Al(OH)₄^-] + 2 [Al₂(OH)₂⁴⁺] + 3 [Al₃(OH)₄⁵⁺] = [Al³⁺] + [AlOH²⁺] + [Al(OH)₂⁺] +

+ [Al(OH)₃] + [Al(OH)₄^-] + [(1/2) Al₂(OH)₂⁴⁺] + [(1/3) Al₃(OH)₄⁵⁺].

Логарифм суми приблизно дорівнює логарифмові найбільшого доданка.

На рис. 1 та 2 графіки логарифмів розчинності наведено жирними лініями. З графіків можна оцінити область мінімуму (значення рCl чи рН), де найефективніше компонент відокремлюється з розчину. Графік

lg [(m / i) M_iL_j] = lg (i / m) + lg [M_iL_j] (19)

іде паралельно графікові lg [M_iL_j] на відстані lg (i / m). Тоді, представляючи lg S як верхню обвідну, слід брати графіки логарифмів рівноважних концентрацій еквівалентів. Користуємось нагодою підкреслити гнучкість поняття еквівалентів. Всупереч традиціям, його можна вживати й при (m / i) > 1.

Умови переважання у гомогенних системах. Розглянемо області pH, де переважають продукти кислотно-основних перетворень,

H⁺ + Ac^-  HAc, lg K_Н = 4,76,

оцтової кислоти. Згідно ЗДМ,

[HAc] / {[H⁺] [Ac^‑]} = K_Н, [HAc] / [Ac^‑] = K_Н [H⁺].

Там, де переважає HAc, тобто там, де [HAc] > [Ac^‑], маємо

[HAc] / [Ac^‑] = K_Н [H⁺] > 1, lg {K_Н [H⁺]} > 0, lg K_Н + lg [H⁺] = lg K_Н − pH > 0, lg K_Н > pH.

Там, де переважає Ac^‑, тобто там, де [Ac^‑] > [НAc], маємо

[HAc] / [Ac^‑] = K_Н [H⁺] < 1, lg {K_Н [H⁺]} < 0, lg K_Н + lg [H⁺ ] = 

= lg K_Н – pH < 0,

lg K_Н < pH.

Можна знайти межі цих областей, де

[HAc] = [Ac^‑], [HAc] / [Ac^‑] = K_Н [H⁺] = 1, lg {K_Н [H⁺]} = 0, lg K_Н + lg [H⁺] = lg K_Н – pH = 0, lg K_Н = pH.

Неважко визначити, що переважає права сторона й ліва сторона цієї межі. Зі спадом рН (зростанням [H⁺]) рівновага реакції зміщується праворуч, у бік зв’язування H⁺. Отже, при рН, менших за значення на межі, переважатиме НАс, а при рН, більших за значення на межі, переважатиме Ас^‑.

Зобразимо наочно області переважання на осі рН,

НАс | Ас‑ 0 |  4,76 | 10 | 14 | pH

Тепер розглянемо області переважння продуктів кислотно-основних перетворень фосфатної кислоти. Тут

H⁺ + PO₄^3‑  HPO₄^2‑, lg K_H1 = 12,35,

H⁺ + HPO₄^2‑  H₂PO₄^‑, lg K_H2 = 7,20,

H⁺ + H₂PO₄^‑  H₃PO₄, lg K_H3 = 2,15.

Межею областей для HPO₄^2‑ та PO₄^3‑ є рН = lg K_H1 = 12,35, межею областей для H₂PO₄^‑ та HPO₄^2‑ є рН = lg K_H2 = 7,20, а межею областей для H₃PO₄ та H₂PO₄^‑ є рН = lg K_H3 = 2,15,

Н3РО4 | Н2РО4‑ | НРО42‑ | РО43‑ 0 |  2,15 | 7,20 | 12,35 | pH

Нейтральне середовище відокремлює області переважання H⁺ та OH^‑ – продуктів автопротолізу H₂O,

H₂O  H⁺ + OH^‑,   lg K_w.

Тут немає аналогу M, бо концентрацію H₂O не вводимо до ЗДМ. Залежність [H⁺] та [OH^‑] -

[OH^‑] = K_w / [H⁺],   lg [OH^‑] = lg K_w + pH.

У кислому розчині переважає H⁺, [H⁺] > [OH^‑], у лужному – OH^‑, [H⁺] < [OH^‑], нейтральний є межею,

[H⁺] = [OH^‑],   pH = - (lg K_w) / 2.

Усупереч розповсюдженому твердженню, у нейтральному середовищі не завжди pH = 7, бо на lg K_w^с впливають температура, коефіцієнти активності, розчинник.

Колір індикаторів. Перехідному забарвленню приблизно відповідає окіл межі областей переважання

lg K_Hi − 1 < pH < lg K_Hi + 1.

Ускладнення у визначенні областей переважання

Якщо послідовність усіх N ступінчатих констант спадна,

K₁ > K₂ > . . . > K_N,

то у всіх N+1 реагентів існують області переважання, з межами pL = lg K_i. Якщо ж K_i < K_i+1 (аномальна послідовність), то ML_i не має області переважання. Якщо сусідніми є області переважання ML_i і ML_i+j (j > 1), то

ML_i + j L  ML_i+j,   

lg K = lg _i+j – lg _i = lg K_i+1 + lg K_i+2 + . . . + lg K_i+j,   (lg ₀ = 0),

і, згідно ЗДМ,

lg ([ML_i+j] / [ML_i]) = lg K – j pL.

Межа областей переважання, [ML_i+j] = [ML_i] при pL = (lg K) / j, середньому від логарифмів констант.

Розглянемо приклад – комплекси Ag⁺ із NH₃. Тут lg K₁ = 3,31, lg K₂ = 3,91, отже послідовність констант є аномальною, K₁ < K₂. На допоміжній смузі схеми косим штрихом (\\\ або ///) позначено області, де над AgNH₃⁺ переважають інші комплекси. Згідно ЗДМ, [AgNH₃⁺] < [Ag⁺] при pNH₃ > lg K₁ = 3,31; [AgNH₃⁺] < [Ag(NH₃)₂⁺] при pNH₃ < lg K₂ = 3,91. Ці області перекриваються,

Ag(NH3)2+ | Ag+ 0 | 2 | 4 | 6 | pNH3

//////////////////////////////////|χχ|χχ|\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Отже, у проміжному комплексі AgNH₃⁺ немає області переважання. Реагенти з областями переважання взаємно перетворюються за реакцією

Ag⁺ + 2NH₃  Ag(NH₃)₂⁺, lg ₂ = lg K₁ + lg K₂ = 7,22.

Для [Ag⁺] = [Ag(NH₃)₂⁺], як частинний випадок загальної умови, маємо межу областей, pNH₃ = (lg ₂) / 2 = 3,61.

Алгоритм побудови областей переважання:

1. Знайти межу областей переважання. Для спадної послідовності ступінчатих констант стійкості межі областей дорівнюють lg K_i. Якщо таку послідовність порушено (вона є аномальною), то проміжні комплекси ніде не переважають. Межі комплексів, найближчих за складом до ніде не переважаючих, дорівнюють середньому арифметичному логарифмів констант аномальної послідовності.

2. До комплексу МL_і із найменшим числом координованих лігандів L (і = 0 для вільного М) віднести праву область на осі рL; комплексам із зростаючим числом координованих лігандів - області, що послідовно розташовані cправа наліво; пропускаємо комплекси, що ніде не переважають.

КЛД для систем із одноядерними комплексами. Для гомогенних реакцій, змінюючи головну змінну pX = pL (або pH чи pe), міняємо дві залежних змінних – логарифми рівноважних концентрацій двох реагентів, і рівняння прямої вже несправедливе. Наближену асимптоту маємо, приймаючи, що майже весь M перетворився у переважаючий продукт ML_i, і одна із залежних змінних є майже постійною, lg [ML_і]  lg t(M), де t(M) − загальна концентрація компоненту M. Графік іншої змінної стає лінійним. Наближення тим краще, чим глибше ми у області переважання ML_і. У областях для різних ML_і асимптоти різні, й наближений графік - ламана.

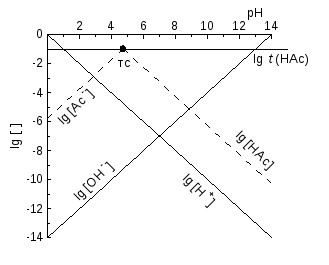
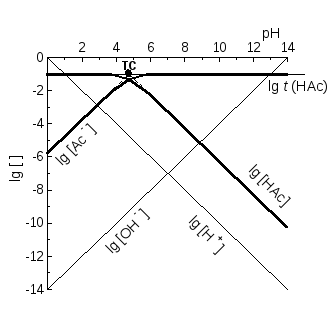
Розглянемо приклад – кислотно-основні перетворення ацетату, t(HAc) = t = 0,10 моль/л. HAc переважає, якщо pH < lg K_Н = 4,76. Для [HAc]  t(Ac^‑) = t наближеним графіком є lg [HAc]  lg t, горизонтальний промінь від (-) до так званої точки системи (ТС), із абсцисою lg K_Н. Правіше за неї переважає Ac^-, [Ac^‑]  t = 0,10 моль/л, і, згідно ЗДМ

lg [HAc] = lg K_Н + lg [Ac^-] – pH  lg K_Н + lg t – pH,

асимптота, промінь униз під кутом 45 ^о (тангенс ‑1) із ТС – кінця горизонтальної асимптоти. Підставляючи pH = lg K_Н у рівняння для lg [HAc], одержуємо lg t. Значить, й ця гілка наближеного графіка йде через ТС.

Алгоритм побудови КЛД для систем із одноядерними продуктами. У простих випадках не записуємо реакцій та ЗДМ. Тангенс кута нахилу є різницею стехіометричних індексів при X у формулах частинок – тієї, що відповідає графіку, й переважаючої у відповідній області.

Так, для lg [HAc] у області переважання HAc лінія горизонтальна, а у області переважання Ac^- тангенс за абсолютною величиною дорівнює 1 (формули Ac^- і HAc відрізняються на 1 H⁺). Знак тангенса такий, що lg [HAc] зменшується, віддаляючись від області переважання HAc: графік не перевищує горизонтальної асимптоти – максимуму функцій! Зломи замінюють плавними спряженнями. На межі областей, де найбільше порушуються наближення lg [HAc]  lg t або lg [Ac^‑]  lg t, речовину з загальною концентрацією t поділено навпіл між НАс та продуктом Ac^‑,

[HAc] = [Ac^‑] = t / 2,   lg [HAc] = lg [Ac^-] = lg t – lg 2,

і згладжені графіки перетинаються нижче за ТС на lg 2  0,3. Для lg [Ac^-] наближений графік – ламана, що складена з асимптот – від ТС до горизонтальної) і від –  до ТС (з тангенсом кута нахилу 1).

КЛД, рис. 3, доповнено графіками lg [H⁺] і lg [OH^-]. Пряма lg [H⁺] йде через початок координат, а lg [OH^‑] – через точку (pH = ‑lg K_w, 0). Тангенси їх кутів нахилу відповідно дорівнюють (‑1) й 1.

Там, де більше двох областей переважання, для кожної – інше наближене рівняння, пов’язане з ЗДМ реакції перетворення переважаючого реагенту (скажімо, ML_і), у той, графік якого досліджуємо (скажімо ML_k),

ML_i + (k - i) L  ML_k,    lg _k – lg _i.

lg [ML_k] = (lg _k – lg _i) + lg [ML_i] + (i – k) pL  

 (lg _k – lg _i) + lg t(M) + (i – k) pL .

Щоб координати точок перетину відрізків не знаходити з рівнянь, зауважимо, що функція неперервна, а графік наближеної функції – ламана зі зломами на межах областей переважання. Графік почнемо із горизонтального відрізка між ТС і продовжимо похилими відрізками в інші області переважання. Отже, алгоритм побудови КЛД:

• Обчислити значення головної змінної pL на межах областей переважання окремих частинок.

• Нанести на діаграму точки системи (ТС) з абсцисами, що обчислені на кроці 1, і ординатою lg t(M).

• Почати наближений графік lg [ML_k] із відрізка, кінці якого у ТС на межах області переважання ML_k, а для частинки, що не має області переважання – у ТС на межах областей переважання частинок, найближчих за складом до розгляданої.

	a
	b

Рис. 3. КЛД для кислотно-основних перетворень ацетату, t(HAc) = t = 0,10 моль/л: (а) ескіз перед побудовою спряжень; (б) КЛД.

Продовжити графік lg [ML_k] ламаною у область переважання ML_і. Тангенс кута нахилу відрізків ламаної дорівнює (i – k), різниці стехіометричних індексів при L для частинки ML_і, що переважає у відповідній області, та ML_k. Кінці відрізка – на межах областей (під ТС).

Якщо точність графіків у околі ТС недостатня для аналізованої проблеми, то замінити зломи плавними спряженнями, точка перетину яких відхиляється на  = ‑ lg j за ординатою від зламу, де j – число сортів частинок, концентрації яких великі й майже рівні у ТС.

Алгоритм зручніший, ніж для гетерогенних систем. Лише за ступінчатими константами відтворюємо (навіть в уяві!) графіки для найбільших концентрацій – горизонтальні відрізки та похилі, що безпосередньо від них відходять.

Щоб вирішити більшість проблем, потрібно розглядати лише декілька найбільших концентрацій, інформація про які міститься у верхній частині КДД, а подробиці поведінки графіків біля ТС неістотні. Часто достатньо горизонтальних і перших похилих відрізків, без 5-го кроку.

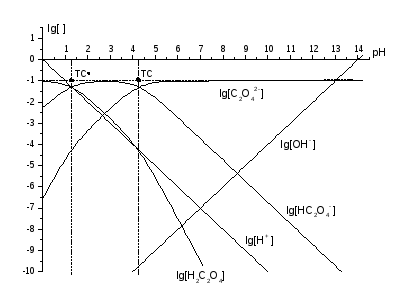
Рис. 4. КЛД для кислотно-основних перетворень оксалату, t(H₂С₂О₄) = t = 0,10 моль/л.

Розглянемо КЛД для Н₂С₂О₄, t(Н₂С₂О₄) = t = 0,10 моль/л, головна змінна pH. Для продуктів приєднання іону Н⁺ до іона С₂О₄^2‑: lg K_H1 = 4,266, lg K_H2 = 1,256 [I = 0]. Це рН на межах областей переважання (крок 1). На кроці 2 наносимо ТС із координатами (1,3, ‑1) та (4,3, ‑1), ордината lg t = ‑1. На кроці 3 будуємо наближені графіки. Графік lg [Н₂С₂О₄] починаємо з горизонтального променя на висоті –1, від ‑ до лівої ТС, графік lg [НС₂О₄^‑] – із відрізка між обома ТС, а lg [С₂О₄^2‑] – із променя від правої ТС на +. На кроці 4 графік lg [Н₂С₂О₄] продовжуємо праворуч (де переважає іон НС₂О₄^‑, що відрізняється від Н₂С₂О₄ на іон Н⁺) відрізком із тангенсом кута нахилу (‑1). Напрям ухилу є очевидним, бо графік порівняно з горизонтальним відрізком може лише спадати. Після правої ТС, де переважає С₂О₄^2‑, графік продовжуємо променем із тангенсом кута нахилу (‑2). Аналогічно будуємо похилі ділянки графіків lg [НС₂О₄^‑] та lg [С₂О₄^2‑], тільки тут вже наявні ділянки зростання функцій. На кроці 5 спрягаємо всі зломи (рис. 4).

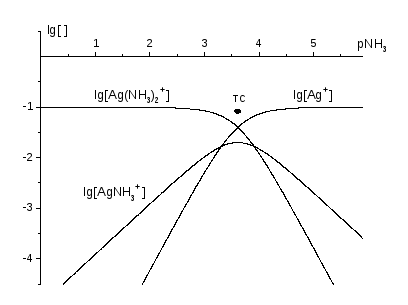
Рис. 5. КЛД для комплексів Ag⁺ із NH₃, головна змінна pNH₃, t(Ag⁺) = t = 0,10 моль/л.

На КЛД для t(Ag⁺) = t = 0,10 моль/л, головна змінна pNH₃, області переважання мають Ag⁺ та Ag(NH₃)₂⁺. Горизонтальні відрізки наближених графіків lg [Ag⁺] та lg [Ag(NH₃)₂⁺] переходять у похилі з тангенсами  2, бо переважаючі комплекси, відокремлені межею, pNH₃ = (lg ₂) / 2 = 3,61, відрізняються на 2 ліганди NH₃. Асимптоти перетинають горизонтальну лінію lg [] = lg t у точках із абсцисами – логарифмами ступінчатих констант. Для AgNH₃⁺ ці точки не співпадають з ТС. Приймимо

lg K₁  lg K₂  (lg ₂) / 2,

бо ступінчаті константи дуже близькі, й проведемо асимптоти графіка lg [AgNH₃⁺] через ту саму ТС двома променями з тангенсами  1. У ТС

lg [Ag⁺] = lg [Ag(NH₃)₂⁺]  lg [AgNH₃⁺]  lg (t / 3) = ‑ 1,5

й спряження проводимо на lg 3  0,5 нижче за ТС.