4.5.4. Построение в плоскости общего положения фигуры заданной формы и размеров
Рассмотрим пример построения в плоскости общего положения Д(αхb) правильного шестиугольника со стороной равной е и с центром в данной точке О. Одна из сторон шестиугольника должна быть параллельна прямой b (рисунок 92).
Прежде чем выполнить необходимые построения, повернем плоскость Д вокруг ее горизонтали h до совмещения с горизонтальной плоскостью Г, проведенной через горизонталь.
Д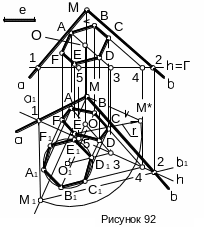
ля
этого построим «совмещенную» проекцию
точки пересечения прямых М, определив
натуру радиуса вращения r
способом прямоугольного треугольника
ОММ*. Соединяя «совмещенную» проекцию
точки М с неподвижными при вращении
точками 1 и 2, получим «совмещенную» с
горизонтальной плоскостью проекцию
плоскости Д. На этой проекции любая
фигура лежащая в плоскости имеет
натуральную форму и размеры. Проекцию
центра О1
шестиугольника находим здесь с помощью
прямой О-3 параллельной заданной прямой
b, лежащей в
плоскости Д и определяемой неподвижной
точкой 3.
Строим правильный шестиугольник с центром в точке О1 и стороной равной е (при помощи окружности радиусом е с центром в указанной точке О1). Расположим шестиугольник так, чтобы одна из его сторон была параллельна прямой b, как того требуют условия задачи. Затем обратным построением находим горизонтальную и фронтальную проекции шестиугольника. Для нахождения проекций его вершин используем прямые плоскости Д, параллельные прямой b и определяемые неподвижными точками 3,4 и 5 горизонтали h.
Анализируя приведенные примеры, можно сделать вывод, что при решении пространственных метрических задач оправдано применение способа дополнительных видов, а при решении плоских метрических и сводимых к ним задач – способа вращения вокруг прямых уровня.
ГЛАВА 5
КРИВЫЕ ЛИНИИ И ПОВЕРХНОСТИ
------------------------------------------------------------------------------------------------
5.1. КРИВЫЕ ЛИНИИ И ИХ ПРОЕКЦИИ
5.1.1. Плоские кривые
Плоской кривой называют линию, все точки которой лежат в одной плоскости, определяемой любыми тремя точками этой кривой и не лежащими на одной прямой.
Наиболее часто встречающимися на практике плоскими кривыми являются кривые второго порядка: окружность, эллипс, парабола и гипербола. Порядок кривой определяется степенью их алгебраического уравнения или максимальным числом точек пересечения ее с прямой. Говоря о кривых второго порядка, имеют в виду, что они пересекаются с прямой не более чем в двух точках. К плоским кривым относятся также различные закономерные кривые: синусоида, циклоида, архимедова спираль и другие.
Известные свойства параллельного проецирования позволяют установить, какие свойства кривых сохраняются у их проекций. Так касательная к кривой проецируется как касательная к ее проекции, а линия пересекающая плоскую кривую– как пересекающая проекцию плоской кривой. При этом число точек пересечения с кривой сохраняется, что означает, что порядок плоской кривой при параллельном проецировании сохраняется.
Кривую линию называют гладкой кривой, если в каждой из ее точек можно провести только одну касательную t, непрерывно изменяющуюся от точки к точке.
Р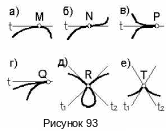
азличают
обыкновенные и особые точки
кривых. На рисунке 93 кроме обыкновенной
точки М, показаны некоторые особые
точки: N- точка перегиба,
Р- точка возврата первого рода, Q-
точка возврата второго рода, R-
узловая точка, Т- точка излома. При
проецировании все эти особенности точек
кривой сохраняются, что позволяет судить
о характере плоской кривой по ее проекции.
Построение проекций плоской кривой линии, лежащей в плоскости общего положения удобно производить при помощи вышеописанного способа совмещения (см. 4.5.4 и рисунок 92). Построение проекций точек кривой линии выполняют так же, как и для точек плоского многоугольника.