7.5. Взаимное пересечение поверхностей второго порядка. Особые случаи пересечения

Линия пересечения поверхностей второго порядка является кривой четвертого порядка, так как известно, что порядок линии пересечения двух алгебраических поверхностей равен произведению порядков поверхностей. Линия четвертого порядка пересекается с плоскостью в четырех точках (действительных и мнимых). В отдельных случаях линия пересечения поверхностей второго порядка может распадаться на несколько частей. Особый интерес представляет случай, когда она распадается на пару плоских кривых второго порядка. В качестве примера рассмотрим пересечение сферы с конусом, имеющим круговое основание (рисунок 158). Здесь линия пересечения распадается на две окружности - АВ и CD. Эти окружности проецируются на фронтальную плоскость проекций в виде отрезков прямых линий, поскольку плоскость симметрии конической поверхности параллельна фронтальной плоскости проекций Ф.

Попробуем определить - при каких условиях линия пересечения двух поверхностей второго порядка распадается на две плоские кривые второго порядка?

И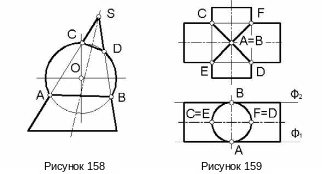 звестно, что если две поверхности имеют в некоторой их общей точке одну и ту же касательную плоскость, то они касаются друг друга в этой точке. Если же две пересекающиеся поверхности имеют две такие точки, то говорят, что они имеют двойное прикосновение.

Линия пересечения двух поверхностей второго порядка, имеющих двойное прикосновение, распадается на две плоские кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки прикосновения (касания).

Доказательство этого положения приведено в книге Н.Ф.Четверухина «Курс начертательной геометрии».

Приведем пример, иллюстрирующий вышесказанное.

Пример 1. Построить линию пересечения двух цилиндров вращения одинакового диаметра (рисунок 159).

Эти поверхности имеют двойное прикосновение в точках А и В, поскольку в указанных точках имеют общие касательные плоскости Ф1 и Ф2. По этой причине линия их пересечения распадается на две кривые второго порядка, которые должны проходить через точки А, В и точки C,D и E,F пересечения контурных образующих цилиндров.

В этом случае линия пересечения будет представлять собой два одинаковых эллипса, большими осями которых будут отрезки CD и EF, а малыми – отрезок АВ. На фронтальной проекции (виде спереди) эти эллипсы проецируются в отрезки прямых, а на горизонтальной проекции (виде сверху) – в окружность, совпадающую с проекцией вертикально расположенного цилиндра.

Рассмотренное положение о двойном прикосновении поверхностей позволяет достаточно просто строить круговые сечения поверхностей второго порядка, если таковые у них имеются.

Для построения кругового сечения какой-либо поверхности нужно провести сферу, имеющую двойное прикосновение с этой поверхностью. Тогда линия их пересечения распадется на две плоские кривые. А поскольку эти кривые расположены на поверхности сферы, то они являются окружностями. Тем самым будут найдены круговые сечения заданной поверхности второго порядка.

Таким образом, для построения круговых сечений поверхностей второго порядка необходимо провести сферу, имеющую двойное прикосновение с данной поверхностью. Линия их пересечения дает два круговых сечения данной поверхности.

Пример 2. Построить круговые сечения эллиптического цилиндра (рисунок 160).

И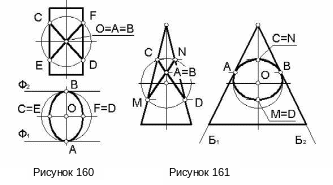 з произвольной точки О оси цилиндра описываем сферу так, чтобы она касалась двух образующих цилиндра и пересекала бы его. Точки касания А и В будут точками прикосновения обеих поверхностей, так как через них можно провести общие касательные плоскости Ф1 и Ф2. Поскольку имеем двойное прикосновение поверхностей второго порядка, линия пересечения их распадается на две плоские кривые. В нашем примере это окружности CD и EF, находящиеся во фронтально проецирующих плоскостях. Любая линия поверхности цилиндра, параллельная указанным окружностям, также будет окружностью.

Пример 3. Построить круговые сечения эллиптического конуса (рисунок 161).

Из произвольной точки оси конуса О опишем сферу так, чтобы она имела двойное прикосновение с поверхностью конуса. В точках А и В у обеих поверхностей общие касательные плоскости Б1 и Б2. В этом случае линия пересечения поверхностей распадается на две окружности CD и MN, расположенные во фронтально проецирующих плоскостях. Полученные круговые сечения входят в две группы круговых сечений конуса, плоскости других круговых сечений параллельны найденным.

Бывают случаи, когда не удается непосредственно обнаружить двойное прикосновение у пересекающихся поверхностей. Тогда чтобы убедиться, что линия их пересечения распадается на плоские кривые, пользуются следующим положением, известным как теорема Монжа и вытекающем из положения о двойном прикосновении:

если две поверхности второго порядка описаны около третьей поверхности второго порядка (или вписаны в нее), то линия их пересечения распадается на две плоские кривые второго порядка.

Покажем применение теоремы Монжа при решении конкретных задач.

Пример 4. Построить линию пересечения конуса и цилиндра, описанных около одной и той же сферы (рисунок 162).

С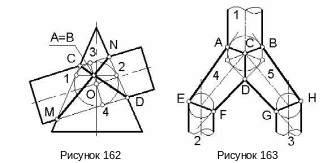 фера касается конической поверхности по окружности 1-2, а поверхности цилиндра по окружности 3-4. Точки А и В пересечения этих окружностей и будут точками двойного прикосновения данных поверхностей, так как в этих точках у конуса и цилиндра будут общие касательные плоскости.

Поскольку имеем дело с двойным прикосновением поверхностей, то линия их пересечения распадается на две плоские кривые второго порядка. В нашем примере это два эллипса CD и MN, фронтальные проекции которых изображаются отрезками прямых.

Пример 5. Построить переходные конические поверхности для разветвления цилиндрического трубопровода 1 на две ветви 2 и 3 (рисунок 163).

Если вписать в каждую из трех труб сферы, то пары сфер 1-2 и 1-3 определят переходные конические поверхности 4 и 5, касательные к этим сферам.

При построении линии пересечения трех цилиндрических труб и переходных поверхностей согласно теореме Монжа определяем, что искомые линии пересечения будут плоскими кривыми (эллипсами). Проекции этих эллипсов будут отрезками прямых, концы которых определяются точками пересечения очерковых образующих.