7.4.2. Способ эксцентрических сфер

Этот способ построения линии пересечения двух поверхностей состоит в применении вспомогательных сфер, имеющих различные центры.

Уточнение условий применения этого способа проведем с помощью примера, аналогичного предыдущему (см. рисунок 155). Там мы выяснили, что центры вспомогательных сфер, пересекающих обе заданные поверхности по окружностям, должны находиться на оси поверхности вращения. Построение линии пересечения в этом случае можно выполнить не только способом концентрических сфер (как в указанном примере), но и способом эксцентрических сфер.

П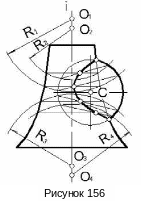 ример 3. На рисунке 156 показано построение точек линии пересечения поверхностей именно способом эксцентрических сфер. При этом проведены четыре вспомогательные сферы радиусов R1, R2, R3 и R4 из различных центров О1, О2, О3 и О4 находящихся на оси i поверхности вращения. Каждая из вспомогательных сфер пересекает данные поверхности по окружностям. Точки пересечения названных окружностей и будут точками искомой линии пересечения поверхностей.

Пример 4. Построить линию пересечения поверхностей тора и конуса вращения, имеющих общую фронтальную плоскость симметрии (рисунок 157).

О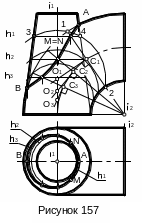 порные точки А и В пересечения контурных линий являются высшей и низшей, правой и левой, а также и точками видимости линии пересечения. Применить для решения данной задачи способ концентрических сфер нельзя, поскольку оси поверхностей i1 и i2 не пересекаются, как необходимо для применения этого способа.

Примем во внимание, что у поверхности тора кроме окружностей, расположенных в плоскостях перпендикулярных оси i2, есть еще семейство окружностей, проходящих через ось i2. Центры сфер, пересекающих тор по этим окружностям, должны находиться на перпендикулярах к плоскостям окружностей, проведенным через центры окружностей С1, С2 и т.д.

Поэтому если брать центры вспомогательных эксцентрических сфер в точках О1, О2 и т.д. пересечения этих перпендикуляров с осью конуса, то сферы проведенные из указанных центров пересекут обе поверхности по окружностям. Точки пересечения окружностей обеих поверхностей, принадлежащие одной и той же сфере, и будут точками линии пересечения поверхностей.

На рисунке 157 проведены три вспомогательные эксцентрические сферы. Случайные точки M и N линии пересечения найдены следующим образом. Сначала в произвольном месте между опорными точками А и В проводим меридиан тора 1-2 (окружность). Из центра С1 восстанавливаем перпендикуляр к плоскости окружности. Центр первой вспомогательной сферы будет находиться в точке О1 пересечения проведенного перпендикуляра с осью конуса. Опишем из этого центра сферу такого радиуса, чтобы она пересекала тор по окружности 1-2. Эта сфера пересечет и поверхность конуса по окружности 3-4. На пересечении окружностей 1-2 и 3-4 получаем пару случайных точек M и N линии пересечения поверхностей.

Для определения горизонтальных проекций точек линии пересечения используем параллели конуса, являющиеся графически простыми линиями (окружностями). Например, горизонтальные проекции точек M и N построены при помощи параллели h1 поверхности конуса.

Два рассмотренных примера показывают, что способ эксцентрических сфер можно применять для построения линии пересечения двух поверхностей, имеющих общую плоскость симметрии; при этом каждая из поверхностей должна содержать семейства окружностей, по которым ее могут пересекать эксцентрические сферы, общие для обеих поверхностей.