Глава 3 метрические задачи. Перпендикулярность прямых и плоскостей

-------------------------------------------------------------------------------------------------

3.1. Определение натуральной величины отрезка и углов его наклона к плоскостям проекций

Задачи, в которых выясняются вопросы измерения длин отрезков и углов, определения натуральной формы плоских фигур и другие называют метрическими задачами.

Указанные задачи можно выполнить с помощью способа прямоугольного треугольника.

П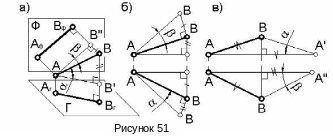 усть дан отрезок АВ общего положения в системе двух плоскостей проекций Г и Ф (рисунок 51а). Переместим горизонтальную проекцию отрезка АгВг параллельно самой себе до совмещения точек А и Аг. Рассмотрим полученный треугольник АВВ'. Этот треугольник прямоугольный, поскольку проецирующие лучи перпендикулярны плоскости проекций. Гипотенузой в нем является сам отрезок АВ, один из катетов равен горизонтальной проекции отрезка, а другой катет – разность высот точек А и В (превышение). Угол α, образованный отрезком АВ и катетом, равным его горизонтальной проекции, является углом наклона отрезка АВ к горизонтальной плоскости проекций.

Аналогично, перенеся параллельно самой себе фронтальную проекцию отрезка АфВф до совмещения точек А и Аф получим прямоугольный треугольник АВВ". Один из катетов этого треугольника будет равен фронтальной проекции отрезка, а другой – разности глубин одного конца отрезка относительно другого. При этом угол β между гипотенузой АВ и катетом, равным фронтальной проекции отрезка есть угол наклона отрезка к фронтальной плоскости проекций.

Таким образом, натуральная величина отрезка является гипотенузой прямоугольного треугольника, у которого одним из катетов будет любая из проекций, а другим катетом соответственно – высота или глубина одного конца отрезка относительно другого.

Прямоугольный треугольник с катетами известной величины можно вычертить в любом удобном в конкретной задаче месте чертежа.

На рисунке 51б показано два варианта построения натуральной величины отрезка АВ. В одном случае прямоугольный треугольник построен на горизонтальной проекции данного отрезка, в другом - на фронтальной проекции. Гипотенузы этих треугольников определяют натуральную величину отрезка АВ, а углы α и β определяют наклон отрезка к горизонтальной и фронтальной плоскостям проекций.

В некоторых случаях удобнее строить прямоугольный треугольник, базируясь не на проекции отрезка, а на высоте или глубине, как показано на рисунке 51в.

Если в качестве первого катета прямоугольного треугольника принять профильную проекцию отрезка, а второй катет взять равным разности широт конечных точек отрезка, то помимо натуральной величины отрезка из указанного треугольника определится угол наклона отрезка к профильной плоскости проекций γ.

3.2. Ортогональная проекция прямого угла

При решении многих задач существенную роль играет знание условий перпендикулярности на чертеже прямых и плоскостей. Выясним свойства ортогональной проекции “прямого угла”.

Если две стороны какого либо угла (в том числе и прямого) параллельны плоскости проекций, то такой угол проецируется на эту плоскость в натуральную величину. Кроме этого случая прямой угол проецируется без искажения (т.е. в свою натуральную величину) и тогда, когда только одна из его сторон параллельна плоскости проекций. При этом вторая сторона угла должна быть не перпендикулярной плоскости проекций.

Верно и обратное положение: если хотя бы одна из сторон угла, проецирующегося ортогонально в прямой угол, параллельна плоскости проекций, то проецируемый угол также является прямым.

Докажем эти положения. Предположим, что в пространстве имеются два отрезка АВ и ВС, расположенные перпендикулярно друг к другу. Иначе говоря, имеем прямой угол АВС. Сторона АВ этого угла параллельна плоскости проекций Г, а вторая сторона ВС не перпендикулярна плоскости Г (рисунок 52).

И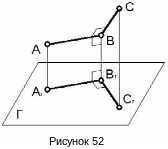 з условия ортогонального (прямоугольного) проецирования следует, что ВВгГ, а так как АВ//Г, то AВВг=90°. Это означает, что прямая ABBВг и ВС, которые лежат в проецирующей плоскости ВССгВг и, следовательно, прямая ABBССгВг.

Но так как АВ//АгВг, то и AгBгВССгВг. Следовательно, АгВгВгСг, т.е.AгBгСг=90º.

Таким образом угол AгBгСг, являющийся проекцией прямого угла АВС, также прямой угол.

Рассмотренные свойства ортогональной проекции прямого угла распространяются как на угол между пересекающимися прямыми, так и на угол между взаимно-перпендикулярными скрещивающимися прямыми.

Для суждения о перпендикулярности скрещивающихся прямых нужно через произвольно взятую точку пространства провести прямые, параллельные скрещивающимся прямым и по углу между этими прямыми делать вывод о взаимном положении данных скрещивающихся прямых.

Обобщая сказанное выше можно сформулировать следующее:

для того чтобы две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) проецировались ортогонально в виде двух взаимно перпендикулярных прямых, необходимо и достаточно, чтобы одна из них была параллельна, а вторая не перпендикулярна плоскости проекций.

Если применить это обобщение к комплексному чертежу, получим следующую формулировку:

две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) только тогда сохраняют свою перпендикулярность на горизонтальной (рисунок 53а,б), фронтальной (рисунок 53в,г) или профильной (рисунок 53д,е) проекции, когда хотя бы одна из этих прямых является соответственно горизонталью, фронталью или профильной прямой.

Р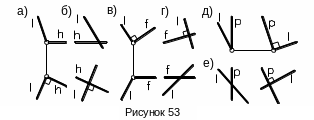 ассмотрим на примерах применение указанных свойств прямого угла.

Пример 1.Определить расстояние от точки А до горизонтали h (рисунок 54а).

Расстояние от точки до прямой определяется перпендикуляром, опущенным из этой точки на прямую.

Г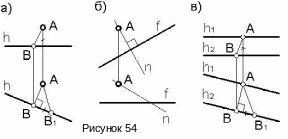 оризонталь является одной из сторон прямого угла и, следовательно, прямой угол с ней будет сохраняться на виде сверху (на горизонтальной проекции), откуда и начинаем решение задачи. Построим здесь перпендикуляр АВ к горизонтали, а затем и на виде спереди (на фронтальной проекции), после чего определяем его истинную величину способом прямоугольного треугольника.

Пример 2. Через точку А провести прямую перпендикулярно фронтальной прямой f (рисунок 54б).

Прямой угол с фронталью сохраняется на виде спереди (на фронтальной проекции), поэтому проводим на этом виде прямую n.

На виде сверху (на горизонтальной проекции) прямая n проводится произвольно, т.к. через точку в пространстве можно провести множество прямых перпендикулярных данной прямой.

Пример 3. Определить расстояние между параллельными горизонталями h1 и h2 (рисунок 54в).

На виде сверху (на горизонтальной проекции) проводим общий для обеих горизонталей перпендикуляр АВ. Для чего на первой горизонтали отмечаем произвольную точку А, из которой опускаем перпендикуляр на вторую горизонталь. Строим его на виде спереди, а затем определяем истинную величину отрезка АВ способом прямоугольного треугольника.