1.3.3. Показатели вариации
Одним из показателей вариации является т.н. вариационный размах, который находится по граничным значениям элементов вариационного ряда:
.
(1.44)
Однако указанный показатель используется сравнительно редко, поскольку во многих случаях верхняя граница вариационного ряда не всегда является показательной. Например, для содержания полезного ископаемого верхней границей может оказаться ураганное его значение. Хотя и существуют способы ограничения проб с ураганным содержанием, но эти способы не всегда эффективны.
В основу вычисления другого показателя вариации входят абсолютные значения разностей (хi – xO):
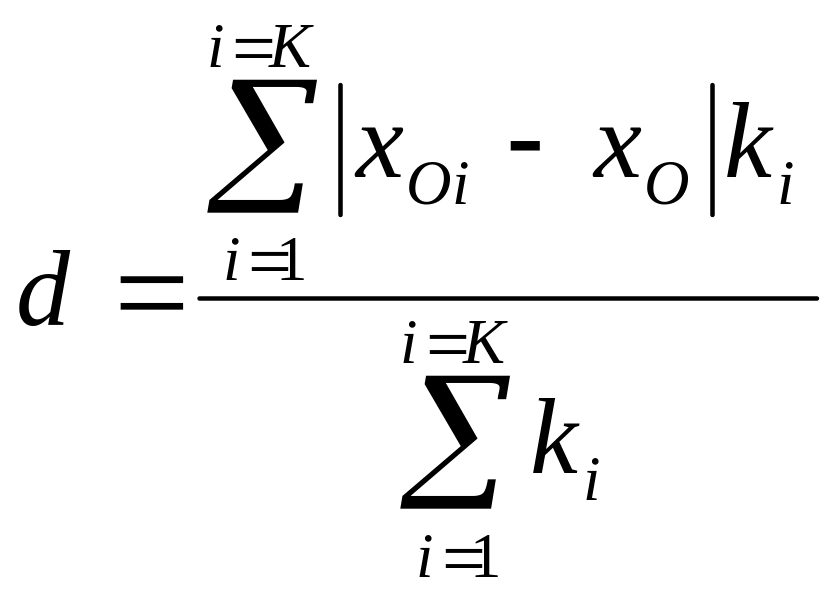или
. (1.45)
Показателями вариации, как мера рассеяния, служат также рассмотренные выше дисперсия и стандарт (среднее квадратическое отклонение).
Часто используют относительный показатель вариации, называемый коэффициентом вариации (обозначается буквой V). Он определяется по формуле
,
(1.46)
т.е. он соответствует отношению стандарта к среднему значению признака. Чаще его выражают в процентах. Иногда коэффициент вариации записывают и в виде простых и десятичных дробей: 1/10, ¼, 0,45 и т.п.
При ограниченном числе наблюдений выполняют оценку надежности коэффициента вариации по формуле
.
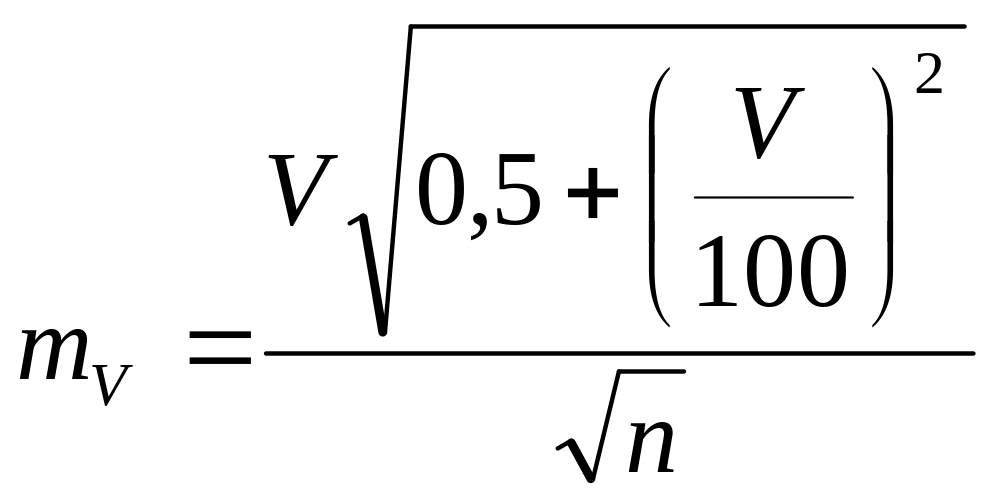(1.47)
Если 3mV < V, то результат считают надежным.
Приведем примеры вычисления показателей вариации для данных, приведенных в табл. 1.2, 1.3, 1.4 и 1.5.
Пример 1.8. Вычислить показатели вариации для данных табл. 1.2 и1.3.
Табл. 1.2.
Размах: R = 886 – 64 = 822 г/м3.
г/м3.
Коэффициент
вариации (по формуле (1.46)):
или 0,54.
Оценка надежности коэффициента вариации по формуле (1.47):
;
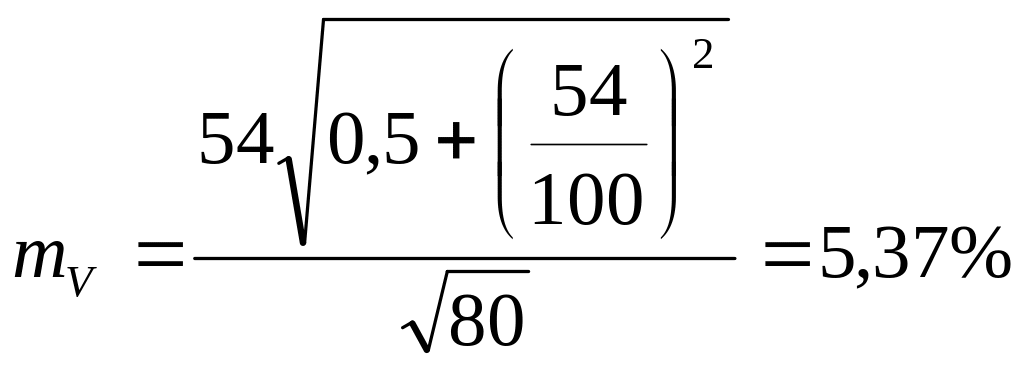3mV = 3·5,37 = 16% < 54%.
Результат надежный.
Табл. 1.3.
Размах (по средним значениям интервалов): R = 818 – 133 = 685 г/м3.
г/м3.
Коэффициент
вариации:
или 0,52.
Надежность
коэффициента вариации:
.
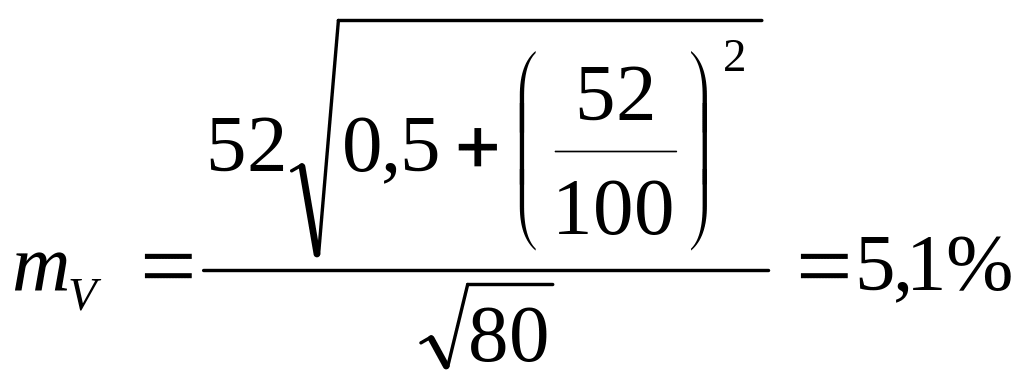Результат надежный.
1.3.4. Медиана и мода
Медианой является значение варианта упорядоченного вариационного ряда, соответствующего его середине.
Если число элементов n ряда нечетное, то медианой является значение варианта с индексом
.
(1.48)
Если число элементов ряда четное, то медиану определяют по среднему арифметическому значению варианов ряда, находящихся в его середине:
.
(1.49)
Примеры определения медианы вариационного ряда.
Пример 1.9. Найти меридиану упорядоченного вариационного ряда, представленного в табл 1.2.
Решение.
Число элементов ряда четное (n = 80). Следовательно, середине ряда соответствуют варианты с номерами 40 и 41: С40 = 309 г/м3; С41 = 326 г/м3.
Ме = (309 + 326):2 = 317,5 г/м3.
Пример 1.10. Найти медиану вариационного ряда, представленного значениями содержания по разведочной линии РЛ№2 (табл. 1.1).
Решение.
Предварительно образуем упорядоченный вариационный ряд: 116, 147, 151, 240, 256, 309, 376, 383, 438 (n = 9).
Медианой, в соответствии с формулой (1.48), является вариант С5 = 256 г/м3.
Кроме указанного приема определения медианы существует и графический способ, о котором будет сказано далее в п. 1.4.3.
Мода характеризует наиболее часто встречающийся вариант в рассматриваемой совокупности. Для дискретного вариационного ряда мода соотвествует примерно середине интервала, имеющего наибольшую частоту. Численное значение моды определяют по формуле:
,
(1.50)
где хmod(min) – нижняя граница модального интервала (в значениях единиц измерения признака); h – ширина модального интервала (в значениях единиц измерения признака); kmod – частота модального интервала; kmod-1 – частота соседнего с модальным интервала, номер класса которого на единицу меньше номера класса модального интервала; kmod+1 – частота соседнего с модальным интервала, номер класса которого на единицу больше номера класса модального интервала.
Пример 1.11. Определить моды интервальных вариационных рядов, представленных в табл. 1.3, 1.4 и 1.5.
Решение.
Табл. 1.3. Модальный интервал соответствует 2-му классу (k2 = 24). Соседние немодальные интервалы имеют k1 = 17 и k3 = 20. Ширина интервала h = 137 г/м3. Нижняя граница модального интервала хmod(min) = 202 г/м3.
Получим:
г/м3.
Табл. 1.4. Модальный интервал соответствует 2-му классу (k2 = 22). Соседние немодальные интервалы имеют k1 = 16 и k3 = 15. Ширина интервала h = 117 г/м3. Нижняя граница модального интервала хmod(min) = 182 г/м3.
Получим:
г/м3.
Табл. 1.5. Модальный интервал соответствует 2-му классу (k2 = 19). Соседние немодальные интервалы имеют k1 = 14 и k3 = 12. Ширина интервала h = 103 г/м3. Нижняя граница модального интервала хmod(min) = 168 г/м3.
Получим:
г/м3.
Необходимо обратить внимание на следующее. В табл. 1.5 усматривается двухмодальное распределение, которое выявилось при разбивке на 8 классов (интервалов): модальный интервал 2 и модальный интервал 4. Вполне вероятно, что это произошло из-за недостатка данных. Однако не исключена и вероятность того, что двухмодальное распределение – закономерное. Например, в рассматриваемом вариационном ряду исследуются элементы, образованные различными объектами (см. рис. 1.1) – двумя продуктивными пластами.
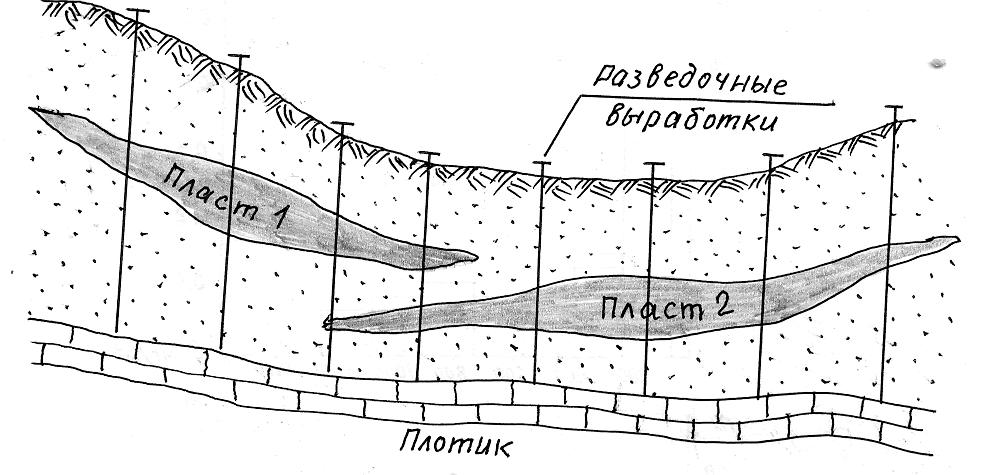
Рис. 1.1. Геологический разрез
Возможны и другие причины. Данный пример приведен для того, чтобы при выявлении каких-либо особенностей в распределении признака исследовались все возможные факторы, которые могут повлиять на вид и характер распределения.