2.5.4. Понятие о множественной регрессии
Множественная регрессия применяется в том случае, когда случайная величина зависит от двух или нескольких случайных величин.
Методы множественной регрессии применяют для прогноза некоторой случайной величины с помощью нескольких независимых переменных, при этом определяют влияние каждой из независимых случайных величин на прогнозируемую величину, считая влияние других на нее ничтожным. Попарное выявление указанного влияния называют парным корреляционным анализом, аналогичным случаю двумерной зависимости, рассмотренной ранее.
Оценки коэффициентов регрессии выполняют по методу наименьших квадратов.
Для определения погрешности аппроксимации множественной регрессии используют формулу
,
(2.78)
где уi – значения прогнозируемой переменной статистической таблицы; уi* - значения прогнозируемой переменной, вычисленные по уравнению множественной регрессии; n – ранг статистической таблицы (число пар переменных; количество измерений; объем выборок); k – число независимых переменных xi , входящих в статистическую таблицу.
В качестве характеристики корреляционной связи между величиной у и всей совокупностью величин х используется коэффициент корреляции между у и у*, который получают по формуле
,
(2.79)
где уo и уо* - соответственно средние значения уi и уi*.
Уравнение множественно регрессии в общем случае имеет вид:
,
(2.80)
где b – постоянные коэффициенты.
Даже при k = 3 определение коэффициентов уравнения множественной регрессии является сравнительно трудоемким.
Для случая трех переменных уравнение множественной корреляции имеет вид
.
(2.81)
Для определения оценок коэффициентов регрессии a, b и c составляют систему нормальных уравнений:
(2.82)
Из решения системы уравнений (2.82) находят искомые коэффициенты и подставляют их в уравнение регрессии (2.81).
Далее приводится пример составления уравнения регрессии при k = 2.
Пример 2.16. Выполнены измерения величин Y, X1 и X2 (см. табл. 2.16 и 2.17). (Результаты измерений условные).
Составить уравнение множественной регрессии, определить коэффициент корреляции и погрешность аппроксимации данных полученным уравнением регрессии.
Таблица 2.16
К примеру 2.16 (исходные данные и расчеты)
№№ пп |
у |
х1 |
х2 |
у1-уо (Δу) |
(Δу)2 |
х1-хо (Δх1) |
(Δх1)2 |
х2-хо (Δх2) |
(Δх2)2 |
(Δу)х х(Δх1) |
(Δу)х х(Δх2) |
1 |
41 |
0,1 |
26 |
-49 |
2401 |
-1,1 |
1,21 |
+7 |
49 |
53,9 |
-343 |
2 |
52 |
0,3 |
22 |
-38 |
1444 |
-0,9 |
0,81 |
+3 |
9 |
34,2 |
-114 |
3 |
58 |
0,2 |
23 |
-22 |
484 |
-1,0 |
1,00 |
+4 |
16 |
22,0 |
-88 |
4 |
75 |
0,6 |
21 |
-15 |
225 |
-0,6 |
0,36 |
+2 |
4 |
9,0 |
-30 |
5 |
87 |
0,9 |
21 |
-3 |
9 |
-0,3 |
0,09 |
+2 |
4 |
0,9 |
-6 |
6 |
103 |
1,4 |
17 |
+13 |
169 |
+0,2 |
0,04 |
-2 |
4 |
2,6 |
-26 |
7 |
106 |
1,6 |
18 |
+16 |
256 |
+0,4 |
0,16 |
-1 |
1 |
6,4 |
-16 |
8 |
114 |
2,0 |
15 |
+24 |
576 |
+0,8 |
0,64 |
-4 |
16 |
19,2 |
-96 |
9 |
124 |
2,1 |
14 |
+34 |
1156 |
+0,9 |
0,81 |
-5 |
25 |
30,6 |
-170 |
10 |
140 |
2,8 |
13 |
+50 |
2500 |
+1,6 |
2,56 |
-6 |
36 |
80,0 |
-300 |
|
900 |
12,0 |
190 |
0 |
9220 |
0 |
7,68 |
0 |
164 |
258,8 |
-1189 |
Средние |
90 |
1,2 |
19 |
|
|
|
|
|
|
|
|
Таблица 2.17
К примеру 2.16 (исходные данные и расчеты)
№№ пп |
у |
х1 |
х2 |
у2 |
х12 |
х22 |
х1х2 |
ух1 |
ух2 |
1 |
41 |
0,1 |
26 |
1681 |
0,01 |
676 |
2,6 |
4,1 |
1066 |
2 |
52 |
0,3 |
22 |
2704 |
0,09 |
484 |
6,6 |
15,6 |
1144 |
3 |
58 |
0,2 |
23 |
3364 |
0,04 |
529 |
4,6 |
11,6 |
1334 |
4 |
75 |
0,6 |
21 |
5625 |
0,36 |
441 |
12,6 |
45,0 |
1575 |
5 |
87 |
0,9 |
21 |
7569 |
0,81 |
441 |
18,9 |
78,3 |
1827 |
6 |
103 |
1,4 |
17 |
10609 |
1,96 |
289 |
23,8 |
144,2 |
1751 |
7 |
106 |
1,6 |
18 |
11236 |
2,56 |
324 |
28,8 |
169,6 |
1908 |
8 |
114 |
2,0 |
15 |
12996 |
4,00 |
225 |
30,0 |
228,0 |
1710 |
9 |
124 |
2,1 |
14 |
15376 |
4,41 |
196 |
29,4 |
260,4 |
1736 |
10 |
140 |
2,8 |
13 |
19600 |
7,84 |
169 |
36,4 |
392,0 |
1820 |
|
900 |
12,0 |
190 |
90760 |
22,08 |
3774 |
193,7 |
1348,8 |
15871 |
Решение.
В таблицах 2.16 и 2.17 выполнены соответствующие расчеты и вычислены суммы по столбцам (выделены в последней строке таблицы).
По формуле (2.5) вычисляем значения стандартов для Y, X1 и X2:
;
;
.
По формуле (2.53) находим значения коэффициентов корреляции между Y и X1 и Y и X2, при этом ковариация определяется по значению (n – 1) :
;
.
Составим систему нормальных уравнений (2.82):
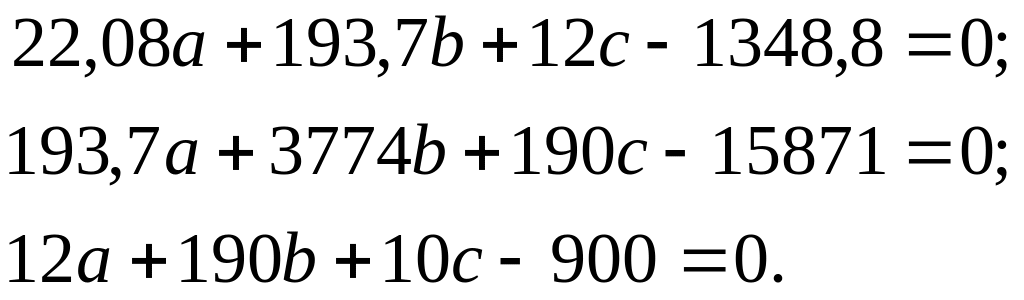
Из решения полученной системы нормальных уравнений получим значения искомых коэффициентов: а = 22,507; b = - 2,829; с = 116,75.
Таким образом, уравнение множественной регрессии будет иметь вид:
у = 22,507х1 – 2,829х2 +116,75. (2.83)
Подставим в уравнение (2.83) значения х1 и х2 из таблицы 2.16 и вычислим значения параметра у* (см. табл. 2.18).
Таблица 2.18
К примеру 2.16
№№ пп |
у |
у* |
у* - уо* (Δу*) |
(у* - уо*)2 (Δу*)2 |
у – у* |
(у – у*)2 |
(у – уо)(у* – уо*) |
1 |
41 |
45,4 |
-44,6 |
1989,16 |
-4,4 |
19,36 |
2185,4 |
2 |
52 |
61,3 |
-28,7 |
823,69 |
-9,3 |
86,49 |
1090,6 |
3 |
58 |
56,2 |
-33,8 |
1142,44 |
+1,8 |
3,24 |
743,6 |
4 |
75 |
70,8 |
-19,2 |
368,64 |
+4,2 |
17,64 |
288,0 |
5 |
87 |
77,6 |
-12,4 |
153,76 |
+9,4 |
88,36 |
37,2 |
6 |
103 |
100,2 |
+10,2 |
104,04 |
+2,8 |
7,84 |
132,6 |
7 |
106 |
101,8 |
+11,8 |
139,24 |
+4,2 |
17,64 |
188,8 |
8 |
114 |
119,3 |
+29,3 |
858,49 |
-5,3 |
28,09 |
703,2 |
9 |
124 |
124,4 |
+34,4 |
1183,36 |
-0,4 |
0,16 |
1169,6 |
10 |
140 |
143,0 |
+53,0 |
2809,00 |
-3,0 |
9,00 |
2650,0 |
Суммы |
900 |
900 |
0 |
9571,82 |
0 |
277,82 |
9189,0 |
Средние |
90 |
90 |
|
|
|
|
|
Используя данные приведенных расчетных таблиц, вычислим по формуле (2.79) значение коэффициента корреляции между исходными значениями параметра Y и значениями того же параметра Y*, вычисленные по формуле регрессии:
.
По формуле (2.78) находим среднюю квадратическую погрешность аппроксимации параметра Y уравнением регрессии:
.