1.6.2. Равномерное распределение

Если плотность вероятностей некоторых случайных величин, составляющих вариационный ряд, будут иметь одинаковые значения в некотором конечном интервале (значений случайных величин), то такое распределение называют равномерным.

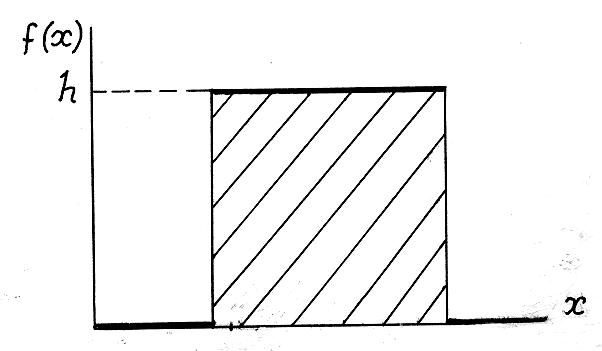
Рис. 1.11. Равномерное распределение

Плотность равномерного распределения случайной величины выражается функцией

f(x) = 0 при х < а и при х > b.

f(x) = h или f(x) = 1/(b – a) при a < x < b, (1.110)

поскольку (площадь под кривой распределения равна 1) – рис. 1.11.

Равномерное распределение является симметричным.

Математическое ожидание случайной величины с равномерным распределением равно середине интервала, в котором распределена эта случайная величина: . Дисперсия . Стандартное отклонение . Медиана равномерного распределения равна математическому ожиданию. При равномерном распределении мода не определяется. Асимметрия A = 0. Эксцесс E = 1,2.

1.6.3. Нормальное распределение

Нормальное распределение является симметричным, т.е. математическое ожидание, мода и медиана равны друг другу. При этом вероятность малых отклонений случайной величины от ее математического ожидания является большой.

Плотность вероятностей случайной величины для нормального распределения имеет вид:

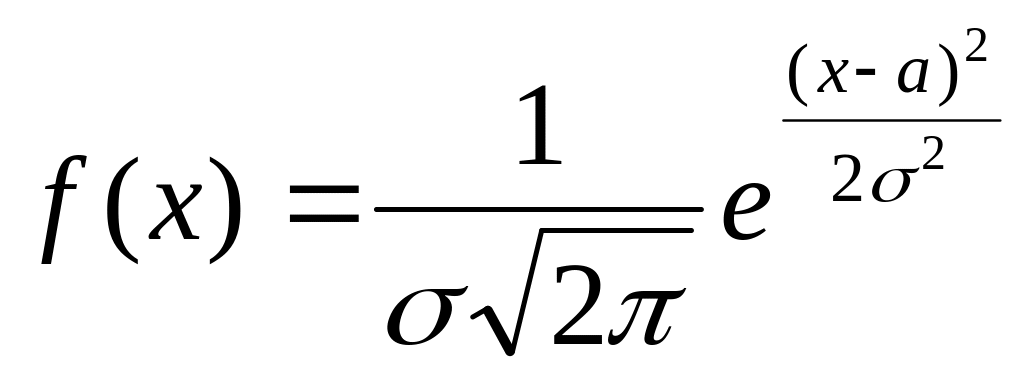, (1.111)

где х – переменная (случайная величина); - стандартное отклонение случайной величины; а = М(Х) – математическое ожидание случайной величины.

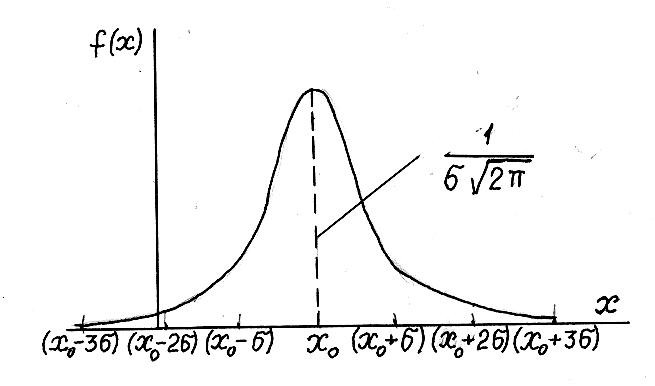
Рис. 1.12. Нормальное распределение

х_о – среднее значение случайной величины;

σ – стандарт случайной величины

Введем обозначение

, (1.112)

которое называется нормированным отклонением. С учетом (1.112) интегральная функция распределения будет иметь вид:

. (1.113)

Вводят обозначение, функцию

, (1.114)

которая называется функцией Лапласа (интеграл вероятностей). Вероятность попадания случайной величины X , которая подчиняется нормальному закону распределения, в интервал определяется с использованием значений функции Лапласа по формуле

Р(а < X < b) . (1.115)

Для удобства вычислений составлены таблицы функции Лапласа (см. приложение 1).

График функции нормального распределения показан на рис. 1.12.

Рассмотрим пример использования таблиц приложения 1 для определения вероятностей.

Пример 1.18. Используя характеристики упорядоченного вариационного ряда (табл. 1.2), полученные при решении примеров 1.2 и 1.6 (среднее арифметическое или математическое ожидание М(Х) = 359 г/м³ ; стандартное отклонение = 194 г/м³) определить вероятность того, что случайная величина попадет в интервал .

При решении данного и последующего примеров принято условие, что анализируемое распределение содержания подчиняется нормальному закону. В действительности, если закон распределения ещё неизвестен, то решать задачу указанным ниже способом нельзя. Предварительно следует установить закон распределения и на основании этого выполнять поставленную задачу.

Решение.

Вычисляем:

; .

По таблице приложения 1 интерполированием находим: Ф(0,5139) = 0,5307; Ф(-0,5795) = -0,5875.

Искомая вероятность р = 0,5( 0,5307 – (-0,5875)) = 0,5591. Практически р = 0,56.

Пример 1.19. Решить ту же самую задачу, но для интервала .

Решение.

Вычисляем:

; .

По таблице приложения 1 интерполированием находим: Ф(-0,5795) = -0,5875; Ф(-0,9940) = -0,8421.

Искомая вероятность р = 0,5( -0,5875 – (-0,8421)) = 0,1273. Практически р = 0,13.