3.5. Допуски результатов измерений и их функций

В любых многократных геодезических и маркшейдерских измерениях могут появиться погрешности, превышающие предельную величину. Такие погрешнсоти относят к грубым и их отбраковывают. Таким образом, грубые погрешности могут быть вызваны не только промахами или просчетами наблюдателя, либо неисправностью прибора. Появление их носит и вероятностный характер. Так, предельную величину погрешности устанавливают часто по правилу «трех сигм» -

. (3.62)

где m – средняя квадратическая погрешность одного измерения. Для ответственных измерений часто для отбраковки результатов, содержащих грубые погрешности, используют коэффициент 2, т.е.

, (3.63)

а в общем случае –

, (3.64)

где t – коэффициент Стьюдента, который устанавливает требуемую вероятность или надежность результатов измерений.

Предположим, что надежность результатов измерений должна быть обеспечена вероятностью p = 0,95 (95%). Тогда по таблице приложения 2 интерполированием получим t = 1,96. В этом случае

. (3.65)

Для исключения погрешностей, превышающих предельное значение, и устанавливают соответствующие допуски.

Пусть известна средняя квадратическая погрешность m одного измерения. Выполнено два измерения одной величины и получена разность d = х₁ – х₂, так называемый размах в результатах измерений. Средняя квадратическая погрешность значения d . Установим доверительную вероятность p = =0,99, для которой t = 2,57. В этом случае допуск по размаху определится как

. (3.66)

То есть условие отбраковки результатов измерений определится неравенством

. (3.67)

Если величина средней квадратической погрешности неизвестна, то ее определяют из многократных измерений по формуле Бесселя (3.10).

Если измерения проводятся в значительно изменяющихся условиях, и точность измерений остается неизвестной, то можно установить условие, при котором обеспечится заданная точность получения среднего значения измеряемой величины.

Предположим, что для среднего значения измеряемой величины задан стандарт М, которого необходимо достичь. Значение средней квадратической погрешности одного измерения оценивается последовательно, по мере накопления результатов, по формуле Бесселя. В этом случае измерения выполняют до тех пор, пока не будет удовлетворено неравенство

. (3.68)

для доверительной вероятности p = 0,99. Значение t_n при p = 0,99 зависит от числа степеней свободы, определяемого как (n – 1) = r. Поэтому значение t_n для установленной вероятности выбирают из таблицы приложения 10 для значений r, а величину t – выбирают из таблицы приложения 2.

Предположим, что задана величина M = 0,005 м для измерения длины линии. Выполнено n = 9 измерений, по результатам которых оценена средняя квадратическая ошибка одного измерения m = 0,015. Установлена доверительная вероятность p = 0,99. Для указанных условий t = 2,57.

Из таблицы приложения 10 t_n = 3,36. После подстановки в формулу (3.68) получим

что говорит о недостаточности числа измерений.

В этом случае можно оценить дополнительное число измерений. Выразим значение n через остальные аргументы:

. (3.69)

После подстановки известных величин получим n_НЕОБХ = 15. Поскольку нами уже выполнено 9 измерений, то дополнительно требуется выполнить еще 6.

Заметим, что, поскольку значение t_n зависит от n, да и средняя квадратическая погрешность тоже будет уточняться с увеличением числа измерений, не целесообразно выполнять сразу все 6 дополнительных измерений. Предварительно можно выполнить, например 3 измерения и снова выполнить оценку по приведенной выше схеме.

Например, дополнительно выполнено 3 измерения, т.е. общее их число стало равным 12. Для новых условий, считая, что m осталась прежней, t_n = 3,115. По правой части формулы (3.68) получим значение 0,0135. То есть выолненного числа измерений все еще недостаточно.

Такой прием носит название способа последовательного анализа.

Часто при массовых измерениях, например, в сетях триангуляции, оценку средней квадратической погрешности измерения угла выполняют по формуле Ферреро:

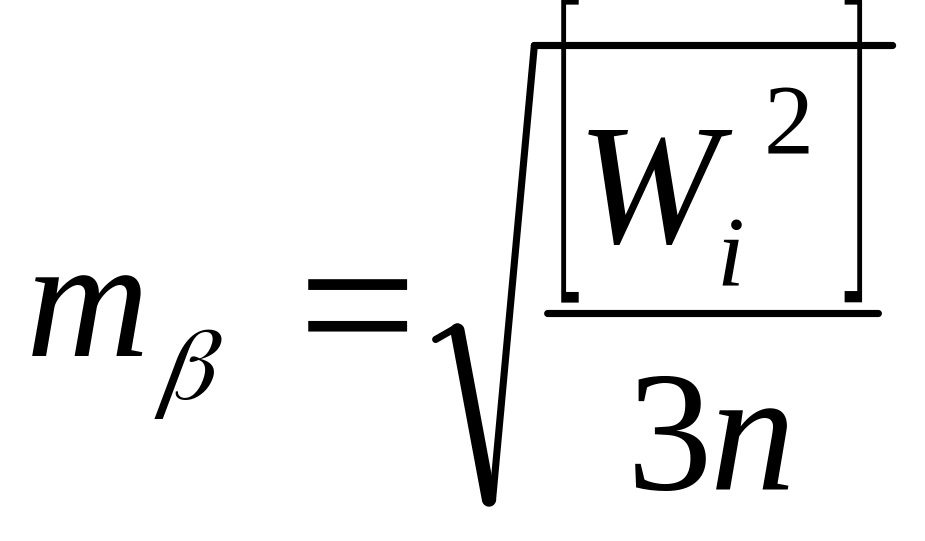. (3.70)

где W_i – невязки в треугольниках; n – число треугольников (невязок), в которых выполнены равноточные измерения углов. При неравноточных измерениях вычисляют среднюю квадратическую погрешность единицы веса функции, т.е. суммы углов треугольника по формуле

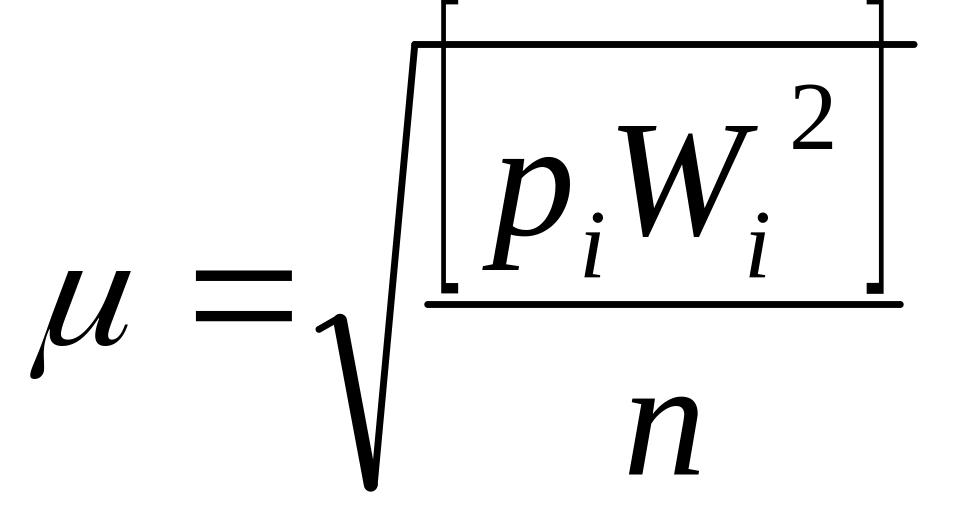, (3.71)

при этом та же формула (3.71) может быть использована и для оценки единицы веса и в других построениях по значениям их невязок.

Пример 3.9. Предположим, что в цепочке треугольников триангуляции n = 5 получены следующие невязки: W₁ = -1,3"; W₂ = +2,2" ; W₃ = +0,8" ; W₄ = -1,7" ; W₅ = -1,5" . Измерения выполнены неравноточно с весами p₁ = 1,5; p₂ = 0,8; p₃ = 0,7; p₄ = 1,8; p₅ = 1,1. Выполнить оценку точности измерения горизонтального угла.

Решение.

В этом случае погрешность единицы веса, т.е. суммы углов в треугольнике с весом, равным 1, определяется по формуле (3.71). Ее значение в данном примере равно 1,7" .

Считая, что в каждом треугольнике углы измерены равноточно, найдем значение средней квадратической погрешности одного угла: .

При многократных измерениях и отбраковке грубых результатов следует иметь в виду, что при установленной доверительной вероятности процент бракуемых результатов не должен заметно отличаться от 100% (1 – p). Например, для доверительной вероятности 0,95 процент отбракованных результатов не должен быть больше 5%. Если он будет значимо отличаться от этой величины, то это говорит о неудачном установлении допусков на результаты измерений.