1.3.2. Дисперсия и среднее квадратическое отклонение

В разделе 1.3.1 говорилось о средней квадратической случайной величины и методе ее определения. Однако для анализа разброса случайных величин эффективно использовать т.н. дисперсию, являющуюся квадратом среднего квадратического отклонения. При использовании дисперсии большие отклонения случайной величины от их среднего арифметического сказываются больше, чем малые.

Классическое определение дисперсии: это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

, (1.32)

где D(X) – дисперсия; Х – случайная величина; М(Х) – математическое ожидание случайной величины (М – знак математического ожидания).

Среднее квадратическое отклонение вычисляют по формулам:

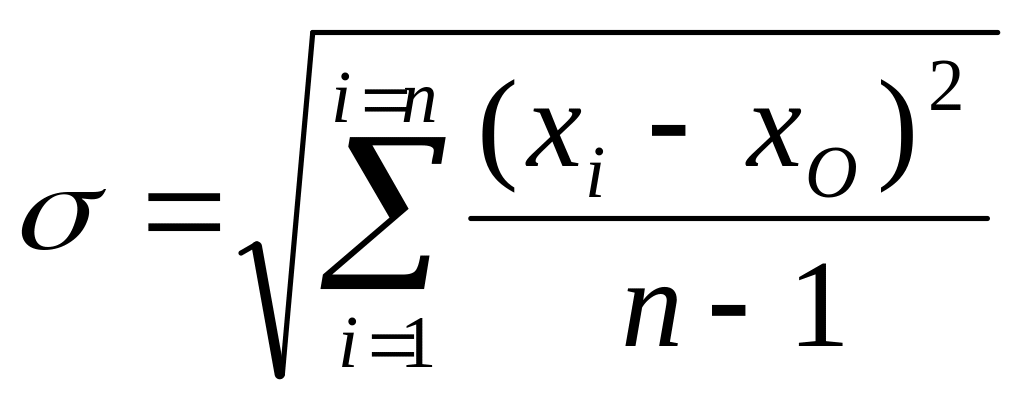(1.33)

при значениях n меньше 20,

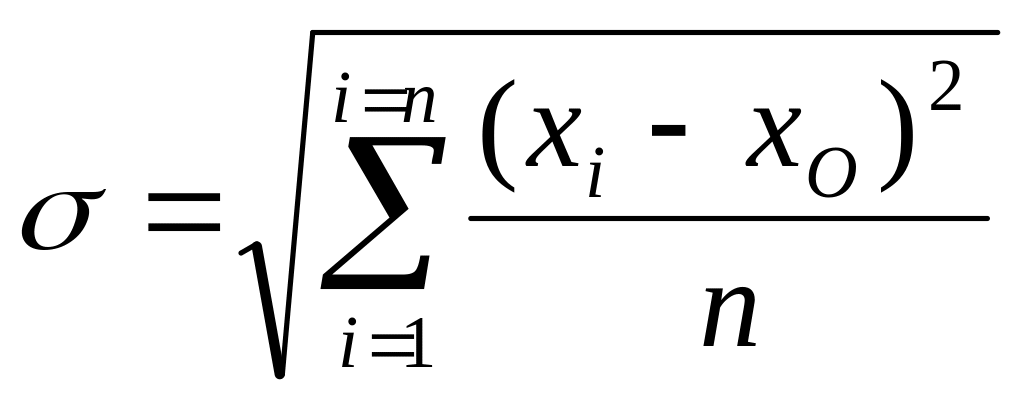(1.34)

при значениях n больше 20,

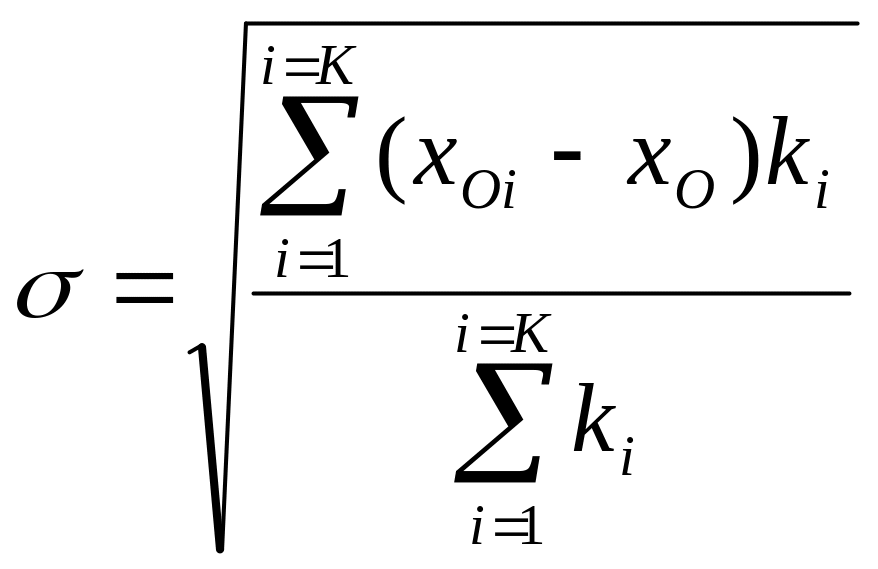, (1.35)

, (1.36)

где х_О – средняя арифметическая вариационного ряда; х_Оi – средняя арифметическая интервала i ; k_i – частота интервала; r_i – относительная частота (частость) интервала; К – число интервалов (классов) вариационного ряда; n – объем совокупности.

В соответствии с определением дисперсии

. (1.37)

При обработке вариационных рядов используют основные свойства дисперсии.

Свойство 1. Дисперсия постоянной величины равна нулю.

Свойство 2. Дисперсия, полученная по квадратам разностей случайной величины с их средней арифметической, является минимальной по сравнению с дисперсиями, вычисленными по отклонениям вариантов от любой другой постоянной величины С, т.е.

< . (1.38)

Свойство 3. Если все варианты х_i уменьшить или увеличить на одно и то же постоянное число С, то величина дисперсии не изменится:

. (1.39)

Свойство 4. Если все варианты уменьшить или увеличить в L раз, то дисперсия соответственно увеличится или уменьшится в L² раз:

, (1.40)

. (1.41)

Свойство 5. Если ряд наблюдений слагается из m групп наблюдений, то дисперсия D всего ряда наблюдений равна сумме внутригрупповой D₁ и межгрупповой D₂ дисперсий:

. (1.42)

Внутригрупповая дисперсия D₁ является средней арифметической всех групповых дисперсий, при этом весами являются также объемы групп.

Межгрупповая дисперсия D₂ определяется по квадратам разностей отклонений средних значений по каждой группе, образующих общую совокупность, от общей средней арифметической х_О всего ряда наблюдений. Весами являются объемы соответствующих групп.

Таким образом, можно записать, что

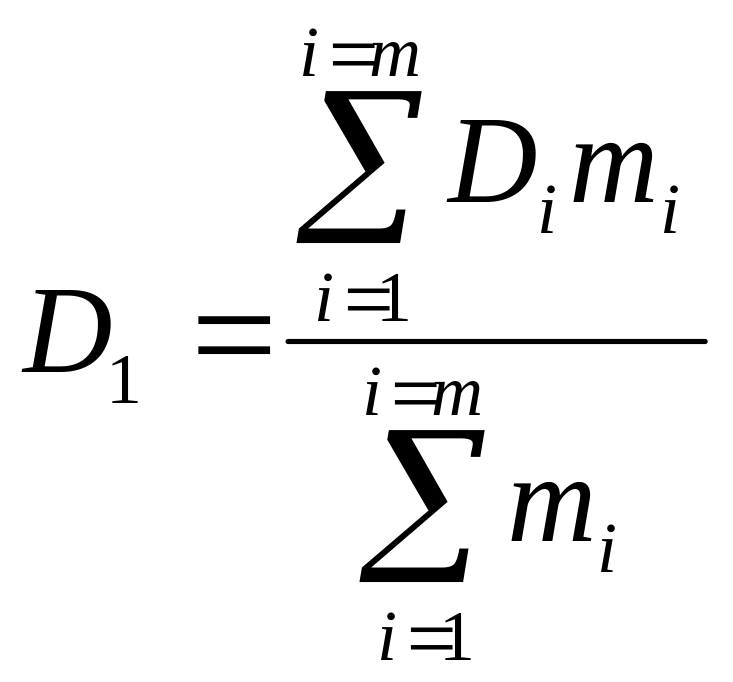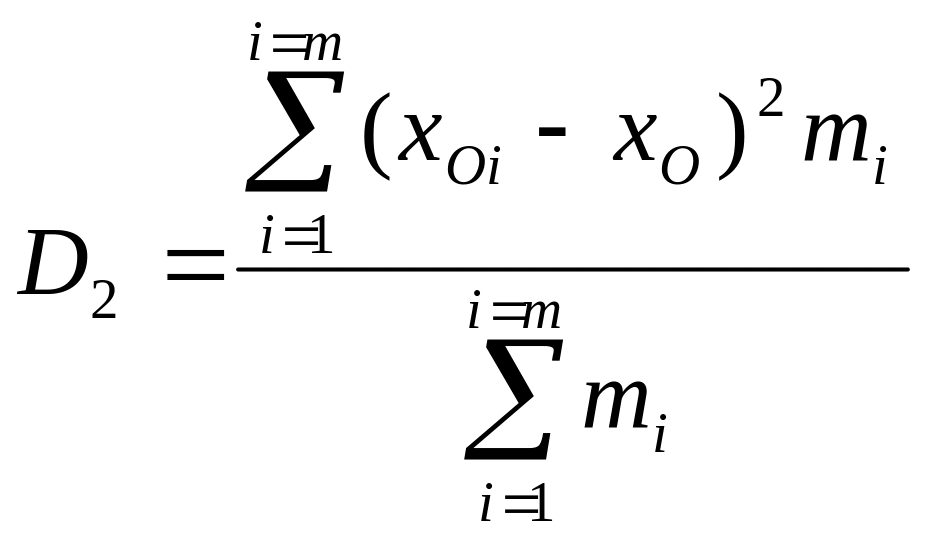, . (1.43)

Пример 1.6. Вычислить средние квадратические отклонения (стандарты) для вариационных рядов табл. 1.2 и интервальных вариационных рядов табл. 1.3, 1.4 и 1.5.

Решение.

В примере 1.2 вычислены средние арифметические для рассматриваемых вариационных рядов. Используем их для вычисления стандартов (средних квадратических отклонений) и дисперсий.

г/м³.

г/м³.

г/м³.

г/м³.

Расхождения, так же, как и при вычислении средних значений содержания, составляют порядка 2%, что объясняется как округлением окончательных значений искомых величин, так и тем, что при вычислениях средних для интервальных вариационных рядов использованы не фактические значения средних, а средние значения интервалов.

D_(1.2) = 194² = 37636. D_(1.3) = 189² = 35721.

D_(1.4) = 198² = 39204. D_(1.5) = 188² = 35344.

Пример 1.7. Вычислить общую дисперсию содержания по двум разведочным линиям (РЛ№1 и РЛ№2), данные по которым приведены в табл. 1.1.

Решение.

Для вычислений используем формулы (1.42) и (1.43).

Количество данных по РЛ№1 m₁ = 7, по РЛ№2 – m₂ = 9.

Среднее арифметическое по РЛ№1 х_О1 = (121+251+…+83):7 = 222,7 = 223 г/м³.

Среднее арифметическое по РЛ№2 х_О2 = (116+256+…+147):9 = 268,4 = 268 г/м³.

Общее среднее весовое по РЛ№1 и РЛ№2 х_О = (223·7 + 268·9):16 = 248,3 = 248 г/м³.

Вычисляем дисперсию по РЛ№1:

.

Вычисляем дисперсию по РЛ№2:

.

Вычисляем внутригрупповую дисперсию: .

Вычисляем межгрупповую дисперсию:

.

Вычисляем общую дисперсию: D = 12810 + 498 = 13308.