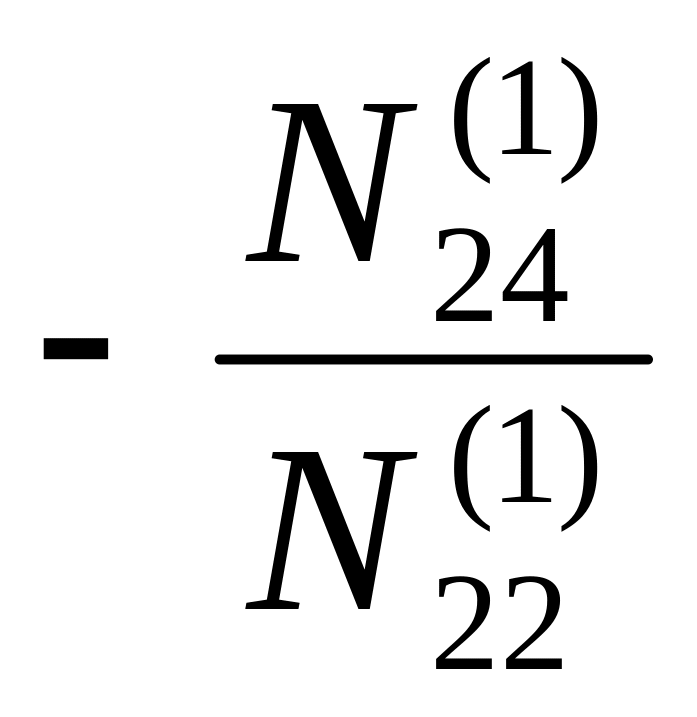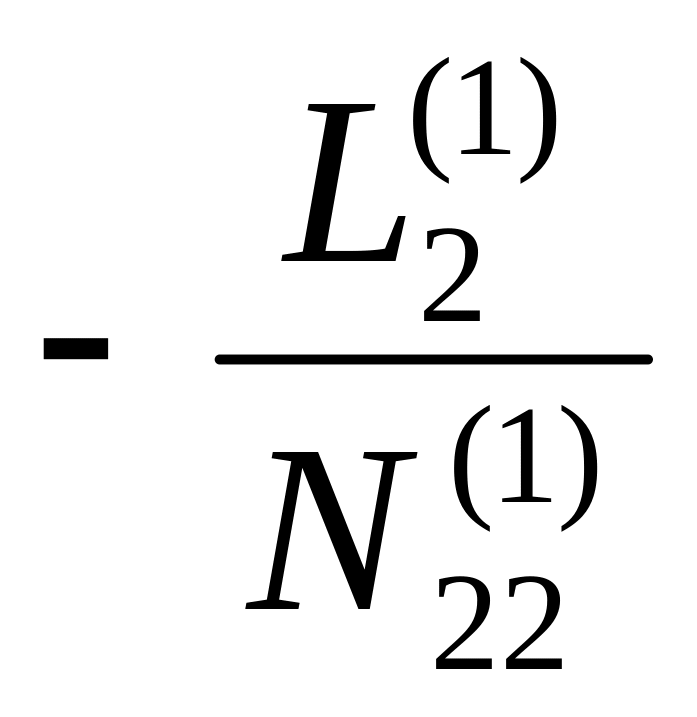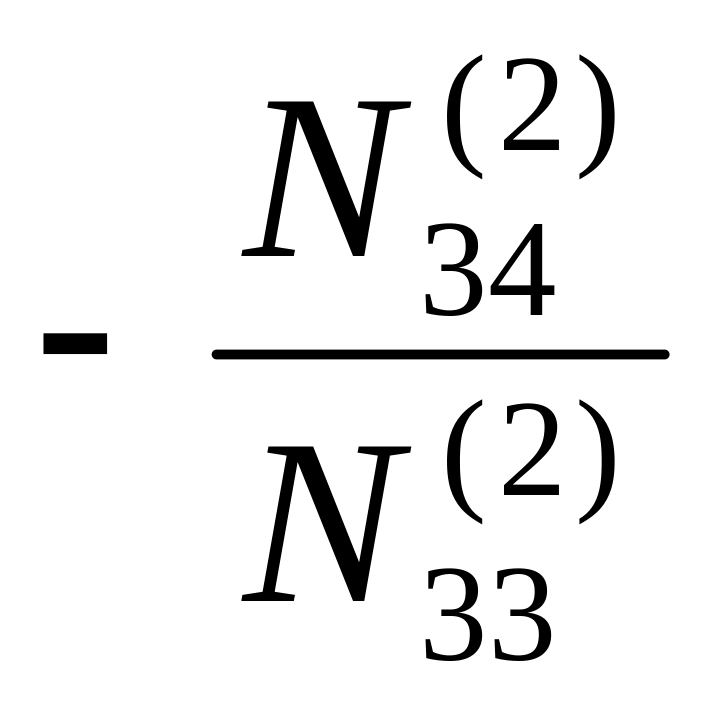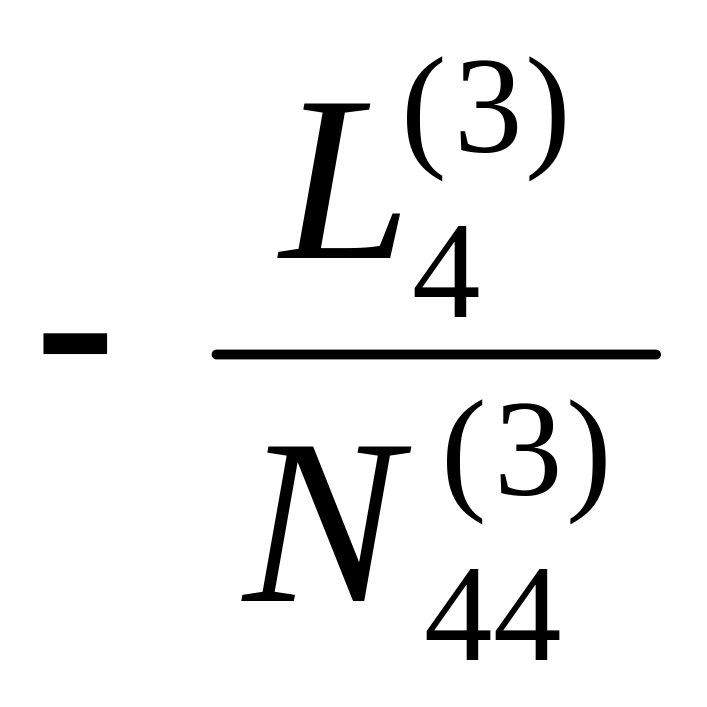4.4.3. Решение систем линейных уравнений по алгоритму Гаусса

В основе алгоритма Гаусса лежит метод последовательного исключения неизвестных, рассмотренный выше. Алгоритм весьма прост из-за простых однотипных действий на каждом последующем шаге вычислений. При этом обеспечивается надежный контроль промежуточных результатов. Кроме того, алгоритм Гаусса упрощает решение систем линейных уравнений при введении в них дополнительных граф, необходимых для вычисления весов уравненных элементов или их функций.

Алгоритм Гаусса рассмотрим на примере системы четырех линейных уравнений вида:

(4.87)

Напомним, что в этой системе линейных уравнений, составленных при решении задачи уравнивания, коэффициенты с одинаковыми двойными индексами являются квадратичными (диагональными). Они всегда положительные и всегда больше любого коэффициента N в своей строке. Коэффициенты, имеющие обратные индексы, равны между собой. В связи с симметрией коэффициентов относительно диагональных таблицу коэффициентов обычно записывают сокращенно в таком виде:

, (4.88)

имея в виду наличие и симметричных коэффициентов на незаполненных местах.

Составим т.н. элинимационное уравнение, которое в алгоритме Гаусса обозначают буквой Е. Это уравнение представляет собой выражение первого неизвестного z₁ через остальные (уравнение Е₁):

. (4.89)

Как выполнялось в методе подстановки, получим новую систему линейных уравнений без неизвестного z₁:

(4.90)

Введем следующие обозначения:

; ;

; ;

; ;

Для полученных коэффициентов сохраняются все особенности системы линейных уравнений с диагональными коэффициентами, имеющими одинаковые двойные индексы (22, 33, 44 и т.д., если уравнений более 4-х). Таким образом, можно записать преобразованную систему линейных уравнений:

(4.91)

Составим второе элинимационное уравнение Е₂ :

. (4.92)

Подставим значение z₂ в уравнения (4.91):

;

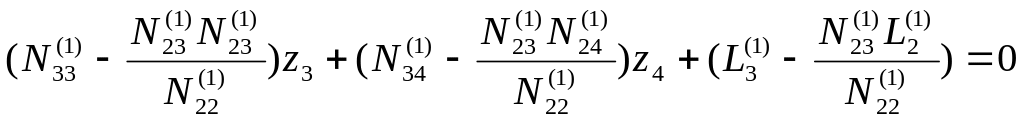. (4.93)

Снова введем обозначения:

; ; ;

;

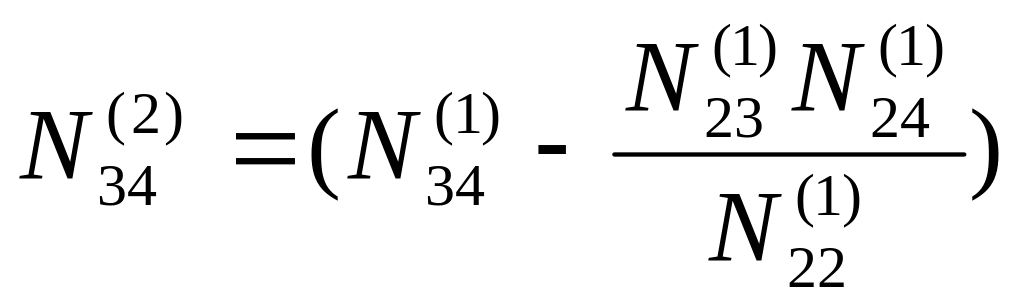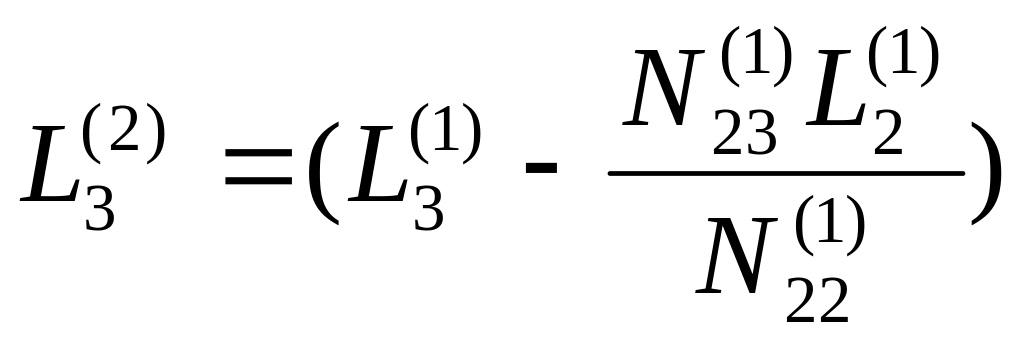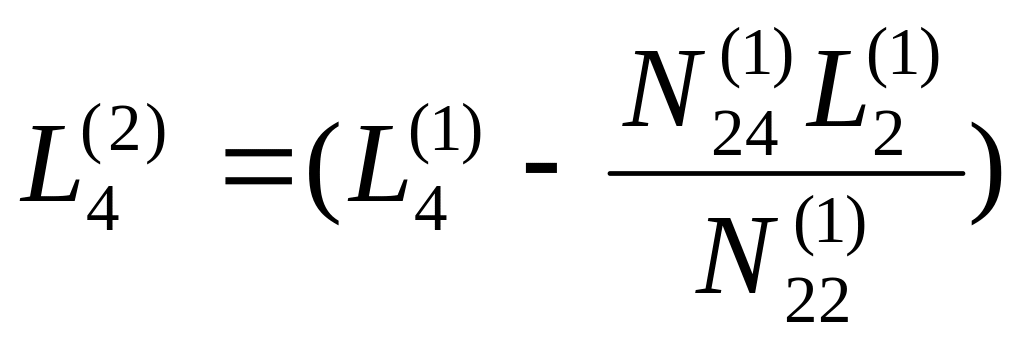
В результате получим систему линейных уравнений с двумя неизвестными:

(4.94)

Третье элинимационное уравнение (Е₃) в этом случае имеет вид:

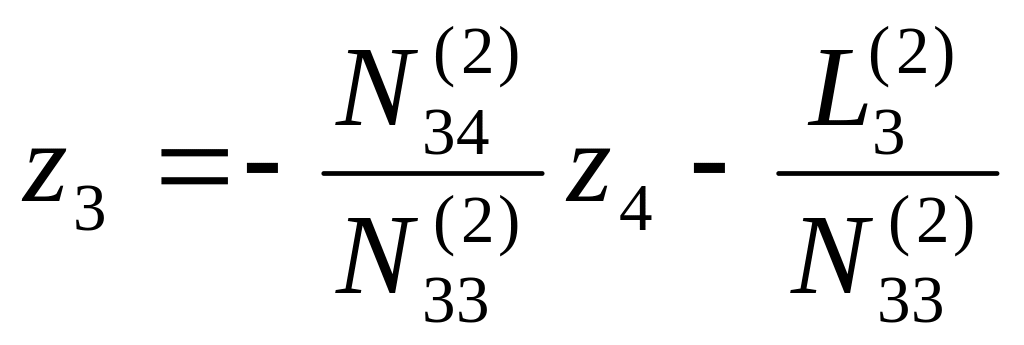(4.95)

Подставим значение z₃ в уравнения (4.94), получим

. (4.96)

Введя в уравнение (4.96) соответствующие обозначения, как и в предыдущих случаях, получим окончательное уравнение с одним неизвестным в обозначениях Гаусса:

(4.97)

Из уравнения (4.97) найдем

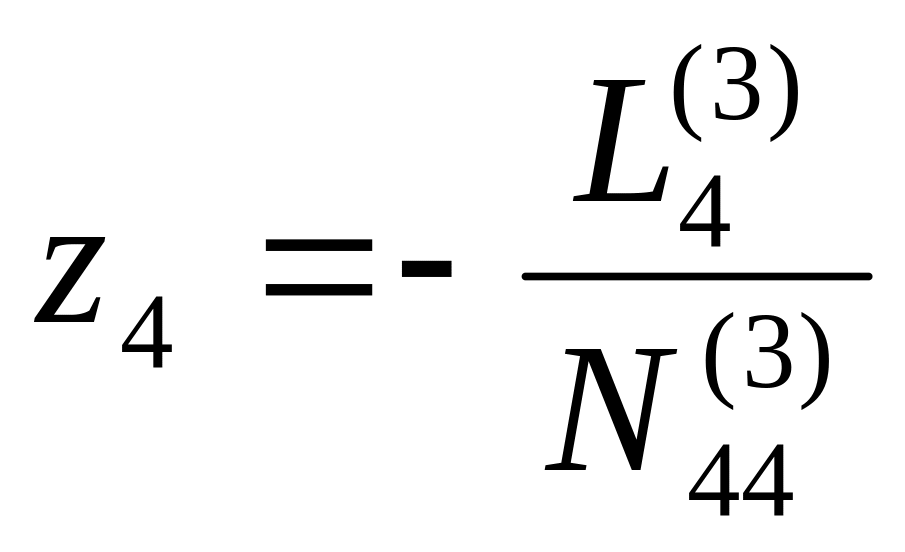. (4.98)

Затем, для определения остальных неизвестных, воспользуемся последовательно элинимационными уравнениями Е₃ , Е₂ и Е₁ , в результате чего получим значения z₃ , z₂ и z₁.

Обратим внимание на то, что для определения неизвестных нужны только элинимационные уравнения. Остальные уравнения не используются.

Представим схему решения системы четырех линейных уравнений в виде таблицы Гаусса (табл. 4.3).

Запись коэффициентов N в строке (3), (7), (12) сокращенная, только вправо от диагональных коэффициентов. Но контрольная сумма этой строки учитывает все коэффициенты, стоящие слева от диагонального. В первой строке записываются все коэффициенты.

После заполнения с вычислениями и контролем строк (1), (2), (3) и (4), что не требует пояснений, заполняют строку (5). Коэффициенты в этой строке равны сумме (3) и (4) строк по столбцам. По аналогии со строкой (2) получают коэффициенты второго элинимационного уравнения Е₂. В строку (7) заносят в сокращенном виде коэффициенты и свободный(ые) члены третьего нормального уравнения. После вычисления строк (8) и (9) по суммам в столбцах строк (7), (8) и (9) получают коэффициенты строки (10). Все дальнейшие действия аналогичны приведенным выше до вычисления коэффициентов в данном случае последнего элинимационного уравнения Е₄. Коэффициент N₅₅ представляет собой указанную в строке (18) сумму произведений весов на квадраты свободных членов. При суммировании столбца по значениям строк (18) – (22) получают значение N₅₅⁽⁴⁾ = [pv²].

Значения неизвестных z_i получают с помощью элинимационных уравнений:

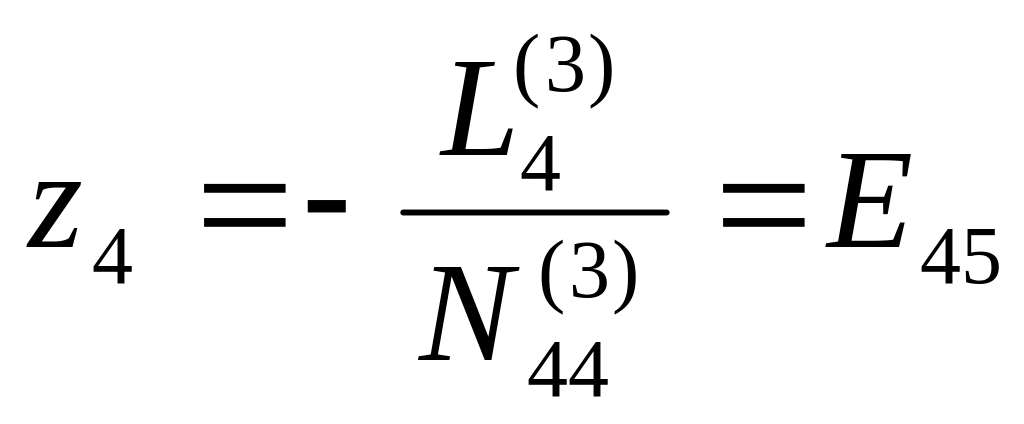
(4.99)

Рассмотрим пример решения системы линейных уравнений по алгоритму Гаусса. Для этого решим систему уравнений (4.68)

1. 4х₁ – 2х₂ + 3х₃ – 2х₄ – 1 = 0

2. - 2х₁ + 5х₂ – 2х₃ + х₄ – 6 = 0

3. 3х₁ – 2х₂ + 3х₃ – 4х₄ – 8 = 0

4. - 2х₁ + х₂ – 4х₃ + 2х₄ + 4 = 0

Решение уравнений выполним по приведенному выше алгоритму в табл. 4.4.

Таблица 4.3

Пример 4.3. Схема решения системы линейных уравнений по алгоритму Гаусса

№№ п/п	Дейст-вия	z1	z2	z3	z4	L	∑
		1	2	3	4	5	6
1	N1	N11	N12	N13	N14	L1	∑1
2	Е1	- 1					∑E1
3	N2		N22	N23	N24	L2	∑2
4	E12N		E12N12	E12N13	E12N14	E12L1	E12∑1
5	N2(1)		N22(1)	N23(1)	N24(1)	L2(1)	∑N2(1)
6	E2		- 1				∑E2
7	N3			N33	N34	L3	∑3
8	E13N			E13N13	E13N14	E13L1	E13∑1
9	E23N(1)			E23N23(1)	E23N24(1)	E23L2(1)	E23∑N2(1)
10	N3(2)			N33(2)	N34(2)	L3(2)	∑N3(2)
11	E3			- 1			∑E3
12	N4				N44	L4	∑4
13	E14N				E14N14	E14L1	E14∑1
14	E24N(1)				E24N24(1)	E24L2(1)	E24∑N2(1)
15	E34N(2)				E34N34(2)	E34L3(2)	E34∑N3(2)
16	N4(3)				N44(3)	L4(3)	∑N4(3)
17	E4				- 1		∑E4
18	N5					[pll]	∑5
19	E15N					E15L1	E15∑1
20	E25N(1)					E25L2(1)	E25∑N2(1)
21	E35N(2)					E35L3(2)	E35∑N3(2)
22	E45N(3)					E45L4(3)	E45∑N4(3)
23	N5(4)					N55(4)	≈ [pv2]

В табл. 4.4 приведен только пример вычисления неизвестных х без оценки точности.

Таким образом, значение х₄ = Е₄₅ = +3,999 ≈ +4.

х₃ = +3,639 ∙ (+3,999) – 11,553 = +2,999 ≈ +3.

х₂ = +0,125 ∙ (+2,999) + 0 + 1,625 = +2.

х₁ = +0,5 ∙ (+2) – 0,75 ∙ (+3) + 0,5 ∙ (+4) + 0,25 = +1.

Таблица 4.4

Пример 4.3. Решение системы линейных уравнений по алгоритму Гаусса

№№ п/п	Дейст-вия	х1	х2	х3	х4	L	∑
		1	2	3	4	5	6
1	N1	+4	-2	+3	-2	-1	+2
2	Е1	-1	+0,5	-0,75	+0,5	+0,25	-0,5 (-0,5)
3	N2		+5	-2	+1	-6	-4
4	E12N		-1	+1,5	-1	-0,5	+1,0 (+1,0)
5	N2(1)		+4	-0,5	0	-6,5	-3
6	E2		-1	+0,125	0	+1,625	+0,75
7	N3			+3	-4	+8	+8
8	E13N			-2,25	+1,5	+0,75	-1,5 (-1,5)
9	E23N(1)			-0,063	0	-0,813	-0,375
10	N3(2)			+0,687	-2,5	+7,937	+6,125(+6,124)
11	E3			-1	+3,639	-11,553	-8,916
12	N4				+2	+4	+1
13	E14N				-1	-0,5	+1
14	E24N(1)				0	0	0
15	E34N(2)				-9,098	+28,883	+22,289(+22,285)
16	N4(3)				-8,098	+32,383	+24,289(+24,285)
17	E4				-1	+3,999	+2,999

Получены такие же ответы, как и при других способах решения указанного уравнения.

Незначительные отклонения от значений вызваны необходимостью округлений промежуточных результатов вычислений.