1.3. Характеристики вариационных рядов

1.3.1. Средние значения признака

При исследовании вариационных рядов пользуются средними значениями признака. Более всего употребляются следующие средние: средняя арифметическая, средняя геометрическая, средняя квадратическая и средняя гармоническая. Средние величины имеют одинаковую с признаком размерность.

Средняя арифметическая вариационного ряда определяется по формуле

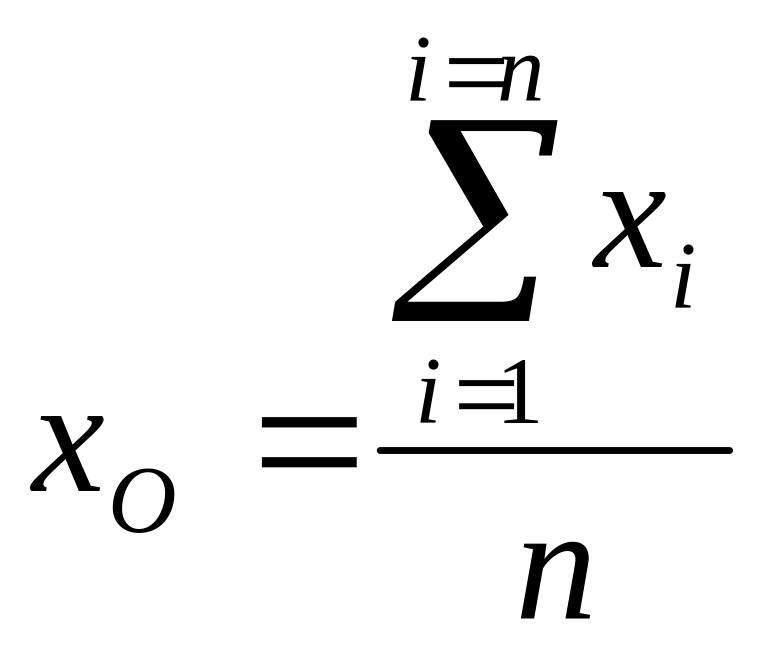, (1.16)

где x_i – элемент вариационного ряда; n – объем совокупности (число элементов ряда).

Для интервального вариационного ряда среднюю арифметическую вычисляют как среднюю весовую (или среднюю взвешенную):

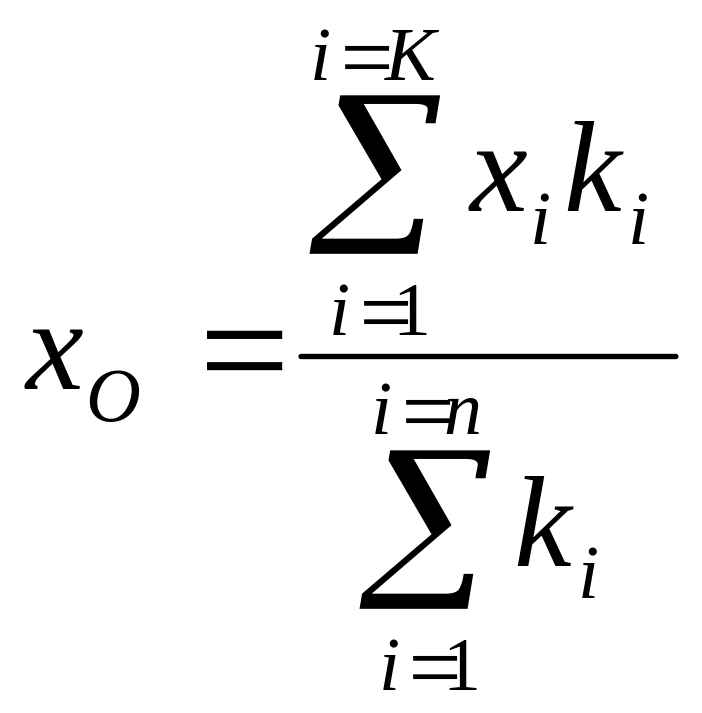, (1.17)

где k_i – частота элементов соответствующего интервала i; K – количество классов (интервалов).

Если в качестве веса класса использовать отностительную частоту (частость) r_i, то формулу (1.17) можно привести к виду

, (1.18)

поскольку .

Особенностью среднего арифметического является то, что

, (1.19)

т.е. при замене каждого варианта х_i на его среднее арифметическое сумма не меняется.

Пример 1.2. Для упорядоченного вариационного ряда, представленного в табл. 1.2 и для интервальных вариационных рядов, представленных в табл. 1.3, 1.4 и 1.5, вычислить значения среднего арифметического и среднего весового с округлением до целого значения содержания.

Решение.

Среднее арифметическое для упорядоченного вариационного ряда (табл. 1.2):

С_О = (65 + 72 + 83 + … + 886) : 80 = 359,3 = 359 г/м³.

Среднее весовое для интервального вариационного ряда (табл. 1.3) по формуле (1.18):

С_О = (132 · 0,21 + 269 · 0,30 + … + 817 · 0,05) = 364,9 = 365 г/м³.

Среднее весовое для интервального вариационного ряда (табл. 1.4) по формуле (1.18):

С_О = (122 · 0,20 + 239 · 0,28 + … + 824 · 0,05) = 360,7 = 361 г/м³.

Среднее весовое для интервального вариационного ряда (табл. 1.5) по формуле (1.18):

С_О = (116 · 0,18 + 219 · 0,24 + … + 837 · 0,02) = 350,8 = 351 г/м³.

Как видим, значения средних арифметических несколько различаются для одного и того же вариационного ряда, представленного в различных видах. Это обусловлено тем, что в вычислениях использованы средние значения в интервалах (классах), а не их фактические значения, вычисленные по значениям вариантов в интервале. Однако следует заметить, что указанные различия являются незначительными и не превышают 3%.

Для непрерывных и дискретных случайных величин среднее арифметическое и среднее весовое называют математическим ожиданием. Математическое ожидание для дискретных случайных величин равно пределу суммы произведений вариантов на их относительные частоты:

при n . (1.20)

Среднее арифметическое, как и математическое ожидание, обладают несколькими свойствами, которые часто применяют на практике. Однако при применении указанных ниже свойств следует иметь в виду, что на практике не достигается строгого их выполнения из-за ограниченного числа наблюдений (из-за ограниченного объема совокупности).

Свойство 1. Среднее арифметическое может быть положительным и отрицательным числом, а также может быть равным нулю.

Свойство 2. Среднее арифметическое суммы нескольких случайных величин равно сумме средних арифметических этих случайных величин.

Свойство 3. Среднее арифметическое произведения двух или нескольких независимых случайных величин равно произведению средних арифметических этих случайных величин.

Свойство 4. Сумма разностей вариантов ряда случайных величин с их средней арифметической равна нулю:

. (1.21)

Для интервального вариационного ряда это свойство записывается в следующем виде:

. (1.22)

Свойство 5. Среднее арифметическаое ряда постоянных чисел равна этому постоянному числу.

Свойство 6. Если все варианты увеличить или уменьшить на одно и то же постоянное число C, то среднее арифметическое также увеличится или уменьшится на это постоянное число:

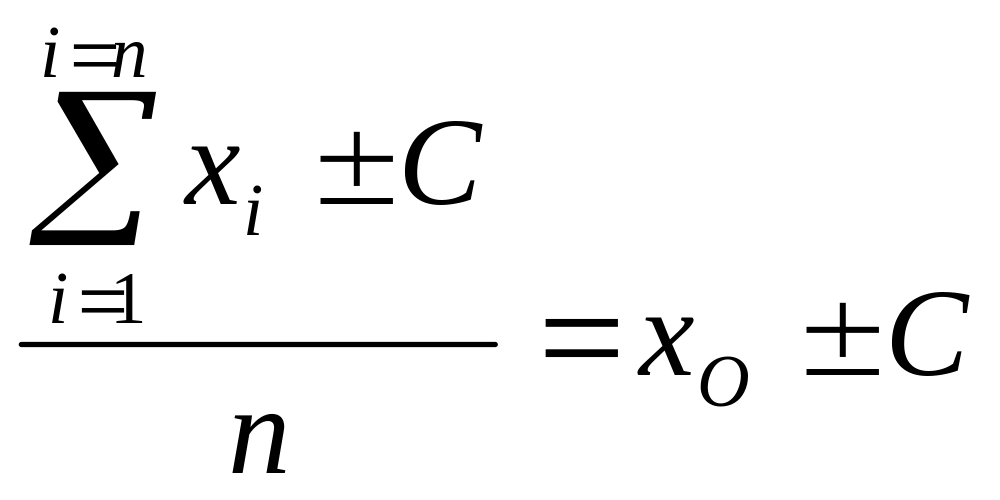. (1.23)

Свойство 7. Если все варианты умножить или разделить на одно и то же постоянное число L, то среднее арифметическое изменится во столько же раз:

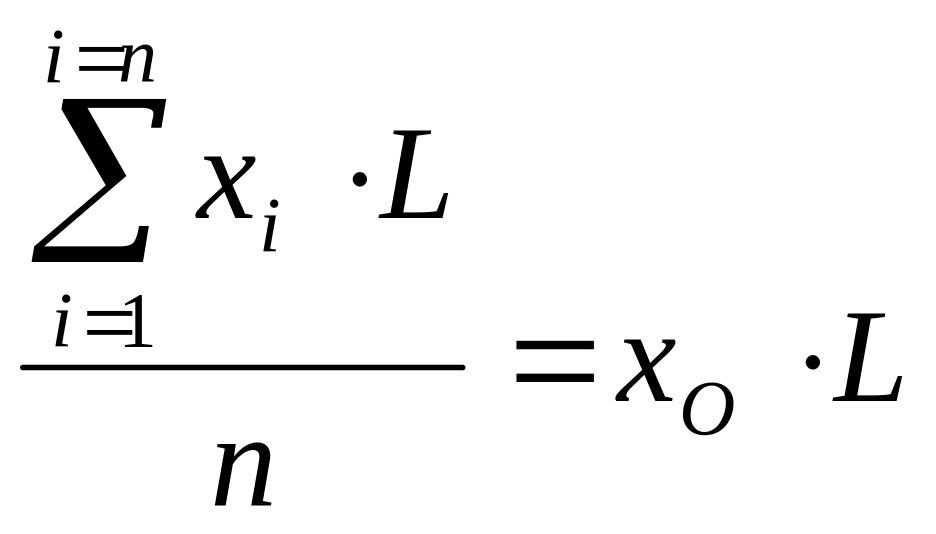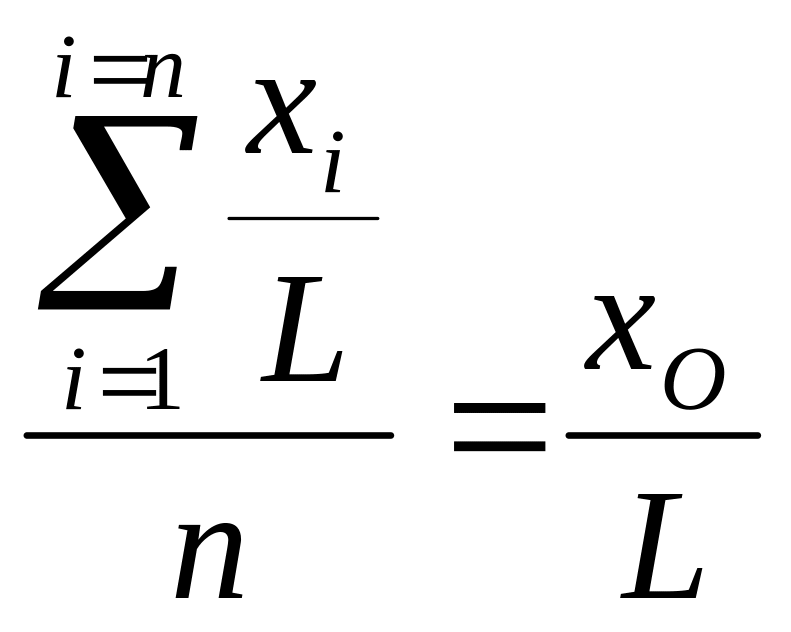; . (1.24)

Необходимость в использовании свойств среднего арифметического на практике обусловлена тем, что элементы исследуемых вариационных рядов могут быть весьма большими по своим значениям либо весьма малыми, поэтому для удобства расчетов их следует привести к удобным величинам. Можно, например, использовать для этого одновременно свойства 6 и 7, образовав новый вариационный ряд

или . (1.25)

Среднее геометрическое вариационного ряда определяется по формуле

, (1.26)

где П – знак произведения вариантов ряда.

Среднее геометрическое для интервальных вариационных рядов определяется по формуле

. (1.27)

Пример 1.3. Вычислить среднее геометрическое для вариационного ряда, представленного в табл.1.2, и интервальных вариационных рядов, представленных в табл. 1.3, 1.4 и 1.5.

Решение.

Для ряда табл. 1.2: г/м³.

Указанные вычисления удобнее выполнять с использованием логарифмов: , а затем уже вычислить искомое среднее.

Для ряда табл. 1.3 (формула (1.27)): x_ГЕОМ = 314,3 = 314 г/м³.

Для ряда табл. 1.4 (формула (1.27)): x_ГЕОМ = 304 г/м³.

Для ряда табл. 1.5 (по формуле (1.27)): x_ГЕОМ = 303,8 = 304 г/м³.

Здесь, как и для средних арифметических интервальных рядов, имеются незначительные расхождения, не превышающие 3%, из-за использования средних арифметических интервалов, вычисленных не по средним арифметическим фактических значений вариантов в интервалах, а по установленным правилам определения границ интервалов.

Средняя квадратическая вычисляется по следующим формулам:

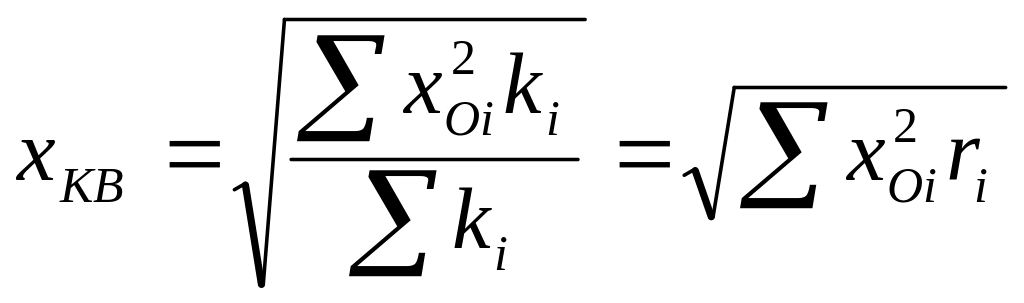; (1.28)

. (1.29)

В формуле (1.28) пределы суммирования от 1 до К (числа классов интервального ряда), при этом x_Oi – среднее арифметическое значений вариантов соответствующего класса. В формуле (1.29) пределы суммирования от 1 до n (объема совокупности).

Пример 1.4. Определить средние квадратические вариационного ряда, представленного в табл. 1.2, и интервальных вариационных рядов, представленных в табл. 1.3, 1.4 и 1.5.

Решение.

Для ряда табл. 1.2: г/м³.

Для ряда табл. 1.3, формула (1.28):

г/м³.

Для ряда табл. 1.3, формула (1.28):

г/м³.

Для ряда табл. 1.3, формула (1.28):

г/м³.

Различия в средних квадратических составляют немногим более 1%.

Средние гармонические вычисляют по формулам:

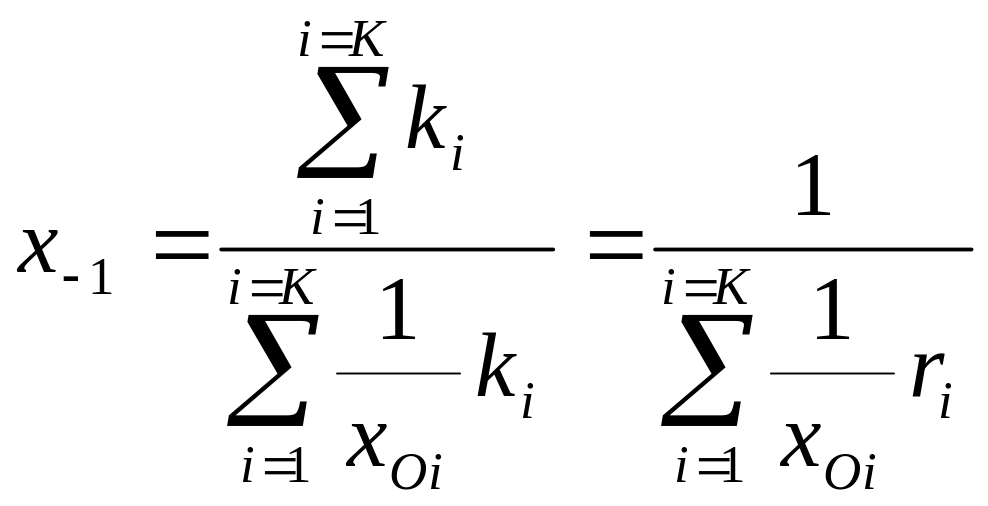; (1.30)

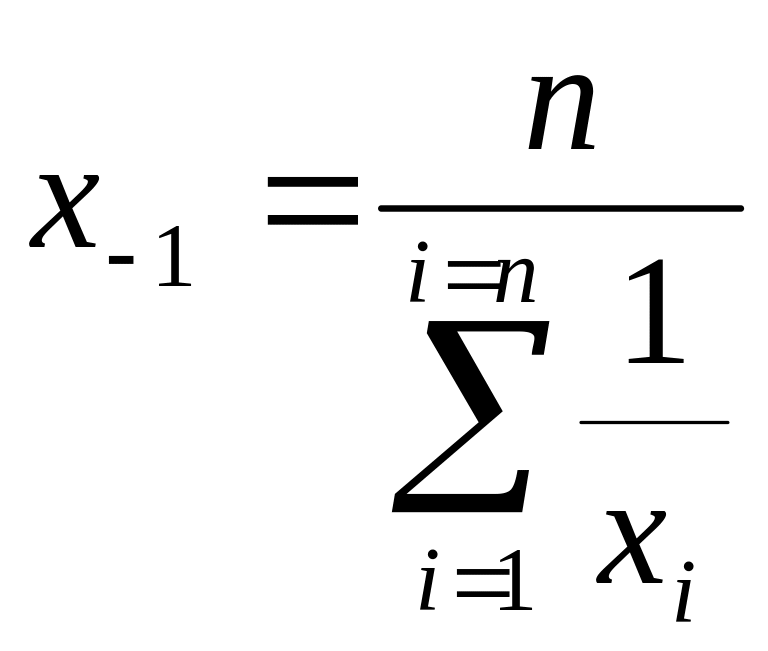. (1.31)

Пример 1.5. Определить средние гармонические для интервальных рядов, представленных в табл. 1.3, 1.4 и 1.5, по формуле (1.30), а также для вариационного ряда табл. 1.2 по формуле (1.30).

Решение.

Для ряда табл. 1.3: 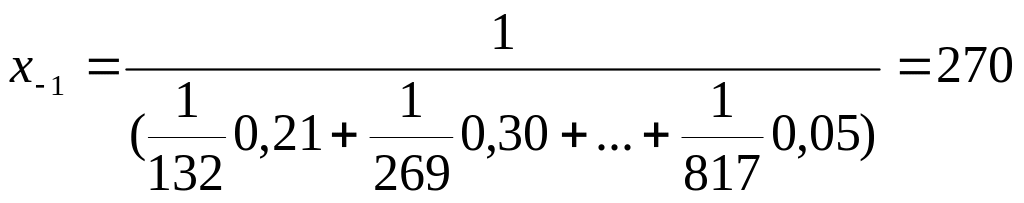г/м³.

Для ряда табл. 1.4: 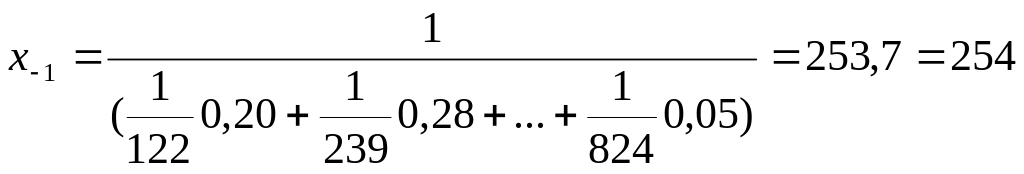г/м³.

Для ряда табл. 1.5: г/м³.

Для ряда табл. 1.2: 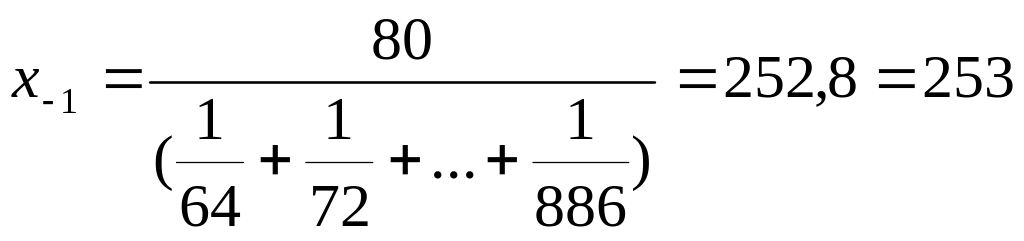г/м³.