4.7.5. Уравнивание направлений в триангуляции
Порядок уравнивания направлений в триангуляции параметрическим способом следующий.
1. Вычисляют предварительные значения координат определяемых пунктов и дирекционные углы сторон сети.
Здесь, с целью уменьшения влияния нелинейностей дифференцируемых функций, необходимо стремиться к тому, чтобы свободные члены уравнений поправок были как можно меньше по абсолютной величине. Этого можно достичь, если предварительно выполнить уравнивание углов в каждом из треугольников. Невязки в них следует распределить с обратным знаком поровну в каждый угол треугольника.
Из решения обратной геодезической задачи находят дирекционные углы и расстояния элементов сети. Предварительные координаты пунктов находят из решения прямых геодезических задач по длинам сторон и дирекционным углам. Значения расстояний находят по теореме синусов, а дирекционные углы – по кратчайшему пути от ближайшей исходной стороны. Если геодезическое построение позволяет использовать для вычисления координат формулы Юнга, то лучше воспользоваться такой возможностью.
2. Определяют коэффициенты a и b уравнений поправок, свободные члены l и составляют параметрические уравнения поправок.
Коэффициенты a и b находят по формулам
;
(4.203)
В формулах (4.203) значения приращений координат берут в километрах. При таком выборе размерностей значения поправок в предварительные координаты получают в децимертах.
Коэффициенты a и b вычисляют с точностью до 0,001 при уравнивании сетей 2 класса и с точностью 0,01 – при уравнивании сетей 3 и 4 классов.
Свободные члены уравнений поправок находят по формуле
,
(4.204)
где
,
(4.205)
(4.206)
В
формулах (4.204) – (4.206)
- предварительное значение ориенти-рующего
угла в пункте k
;
- предварительное значение
дирекционного угла указанного направления
; Mki –
измеренное направление в пункте k
на пункт i
.
Контроль вычисления свободных членов производится по невязкам W по формуле
(4.207)
Кроме того, сумма свободных членов на данном пункте
.
(4.208)
Невыполнение указанных условий не более 0,02" при вычислениях до 0,01" и не более 0,2" при вычислениях до 0,1".
Составляют уравнения поправок
. (4.209)
для всех направлений на данном пункте с учетом того, какой из пунктов исходный и определяемый.
Для упрощения выражений (4.209), уменьшения числа уравнений и исключения из них поправок ориентирования применяют правила Шрейбера.
Правило 1 (исключение поправок ориентирования).
Если
одно из неизвестных в параметрических
уравнениях поправок имеет коэффициент
«минус единица», то для получения
нормального уравнения, не содержащего
этого неизвестного, его можно опустить
в параметрических уравнениях поправок,
добавив к ним сумму этих уравнений
(суммарное уравнение) с весом
, где 1/2 – вес измеренного направления,
n
– число данных направлений.
Пусть имеем несколько (n) уравнений
…………………………………………………….. (4.210)
Тогда можно записать, что
…………………………………………………….. (4.211)
Поскольку на данном пункте должно выполняться условие (4.208), то последнее уравнение в системе уравнений (4.211) будет иметь вид
.
(4.212)
Правило 2.
Если в заданном ряду параметрических уравнений поправок имеются уравнения, различающиеся только свободными членами, то их можно заменить на одно уравнение.
Пусть
…………………… (4.213)
Тогда суммарное уравнение поправок будет иметь вид
.
(4.214)
Правило 3. Приведение весов уравнений к весу, равному единице.
Это правило значительно упрощает дальнейшую вычислительную обработку.
Для
приведения уравнения к весу, равному
единице, необходимо умно-жить его
коэффициенты и свободные члены на
.
Если вес отрицатель-ный, то тоже умножают
на
,
а вес уравнения принимают равным «минус
единице»: р=-1.
Предположим, что имеются уравнения поправок
(4.215)
В этом случае приведенные уравнения поправок (с весом, равным единице) имеют вид
(4.216)
Рассмотрим принцип составления уравнений поправок для схемы триангуляции (рис. 4.15), состоящей из двух треугольников (10 направлений). Пункты 1 и 2 – исходные, пункты 3 и 4 – определяемые.
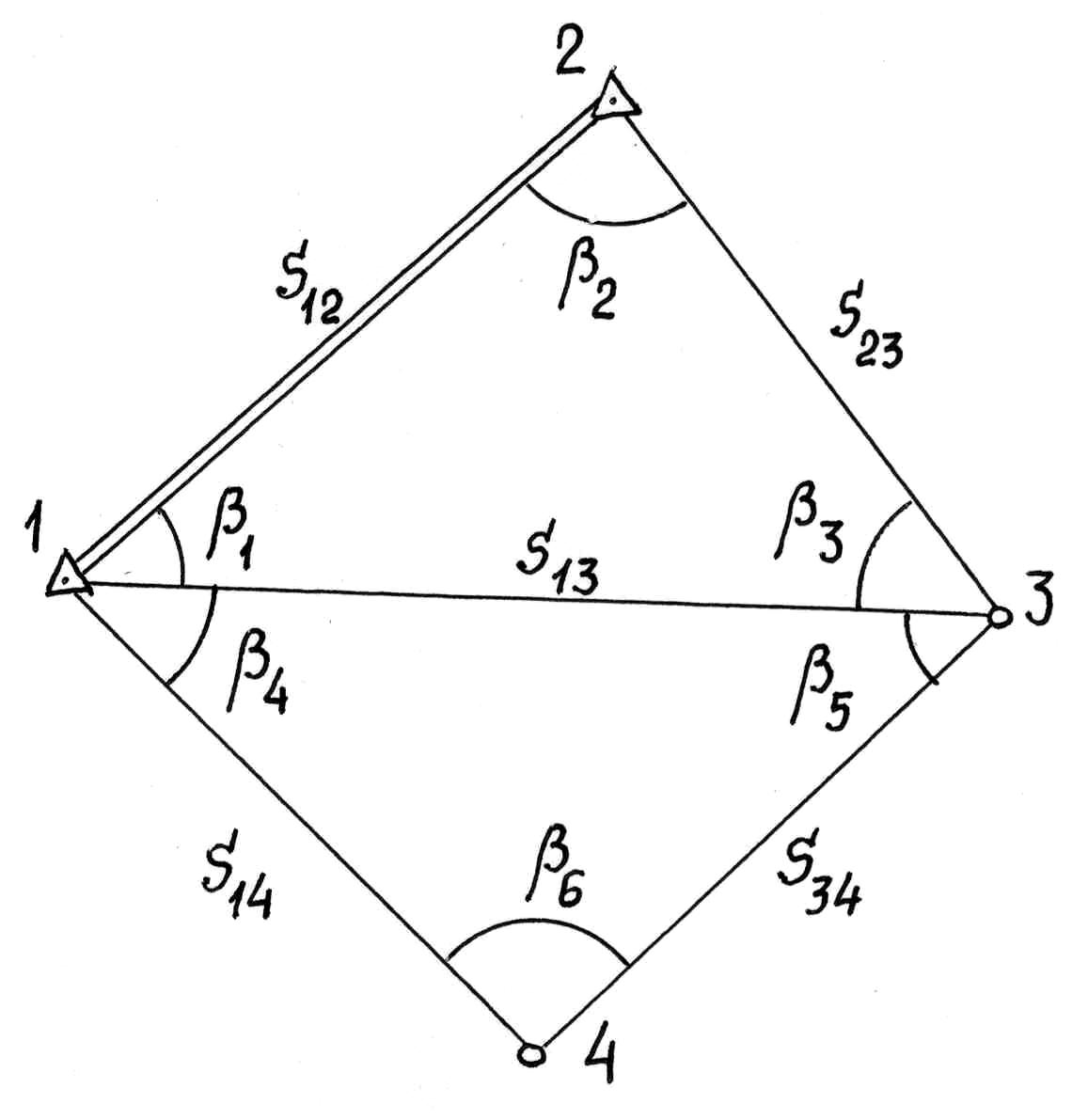
Рис. 4.15. Схема триангуляции
Составим уравнения поправок отдельно для каждого пункта, принимая, что погрешности исходных данных равны нулю.
Пункт 1 (исходный).
1.
2.
3.
Пункт 2 (исходный).
4.
(4.217)
5.
Пункт 3 (определяемый).
6.
7.
8.
Пункт 4 (определяемый).
9.
10.
Применим
для уравнений (4.217) 1-е правило Шрейбера,
т.е. исключим неизвестное
,
принимая во внимание условие (4.216).
Получим:
- пункт 1(исходный):
1.
2.
3.
4.
- пункт 2 (исходный):
5.
(4.218)
6.
7.
- пункт 3 (определяемый):
8.
9.
10.
11.
- пункт 4 (определяемый):
12.
13.
14.
Уравнения 1 и 5 в системе уравнений (4.218) можно исключить, поскольку приведенные поправки являются известными. Кроме того, следует иметь в виду, что при преобразованиях изменяются значения поправок. В связи с этим нами условно приняты такие же обозначения в формулах (4.218), как и в формулах (4.217).
Далее сгруппируем уравнения для взаимообратных направлений и применим к ним 2-е правило Шрейбера. Примем также во внимание, что аik = - aki и bik = bki . Для удобства выполним такие преобразования, чтобы в общих формулах коэффициенты были положительными.
Направление 1-3(3-1):
1.
Направление 1-4(4-1):
2.
Направление 2-3(3-2):
3.
(4.219)
Направление 3-4(4-3):
4.
Остальные уравнения – уравнения сумм в системе (4.218):
5.
6.
7.
8.
Обратим внимание но то, что в системе (4.219) уравнения 3 и 6 можно объединить, используя 2-е правило Шрейбера. Т.е. вместо указанных уравнений записать объединенное –
(4.220)
После составления уравнений поправок в них подставляют вычисленные ранее коэффициенты и свободные члены, для упрощения вычислений все уравнения приводят к весу, равному ±1 (3-е правило) решают уравнения по установленным правилам и вычисляют поправки к предварительным координатам определяемых пунктов ( в рассматриваемом случае – к координатам пунктов 3 и 4).
Все вычисления, связанные с определением уравненных значений результатов измерений и контрольные вычисления выполняются по правилам, изложенным выше.
Далее в примере рассмотрено уравнивание направлений в сети триангуляции, состоящей из двух треугольников, в одном из которых имеется базисная (исходная) сторона, определяемая пунктами 1 и 2 (рис. 4.15).
Таблица 4.60
Значения измеренных направлений и вычисленных горизонтальных углов
Пункт |
Направления |
Значение направления, Mki |
Угол β |
Значение угла |
1 |
1 – 2 |
0о 00' 00,0" |
β 1 |
60о 30' 33,6" |
1 – 3 |
60 о 30' 33,6" |
β 2 |
74 о 50' 09,9" |
|
1 – 4 |
129 о 14' 00,1" |
β 3 |
44 о 39' 17,7" |
|
2 |
2 – 3 |
0о 00' 00,0" |
|
180 о 00' 01,2" |
2 – 1 |
74 о 50' 09,9" |
W(1) |
+1,2" |
|
3 |
3 – 4 |
0о 00' 00,0" |
β 4 |
68 о 43' 26,5" |
3 – 1 |
60 о 58' 03,6" |
β 5 |
60 о 58' 03,6" |
|
3 – 2 |
105 о 37' 21,3" |
β 6 |
50 о 18' 27,5" |
|
4 |
4 – 1 |
0о 00' 00,0" |
|
179 о 59' 57,6" |
4 - 3 |
50 о 18' 27,5" |
W(2) |
-2,4" |
Координаты пунктов 1 и 2:
Х1 = 5364,756 м; Y1 = 4256,214 м; Х2 = 8836,421 м; Y2 = 5748,265 м.
Исходный дирекционный угол α12 = 23о15'25,38", длина исходной стороны (базиса) S12 = 3778,7133 м (из решения обратной геодезической задачи).
В данном геодезическом построении измерены направления в каждом из пунктов (всего 10 направлений) и вычислены углы βi (табл. 4.60).
Все вычисления в примерах будем выполнять на порядок выше, а округлять затем только уравненные величины.
Предварительно выполним следующую обработку в схеме триангуляции: по теореме синусов найдем стороны S23, S14 и S43; вычислим дирекционные углы направлений 2-3, 1-4 и 4-3 через известный дирекционный угол направления 1-2 и вычисленные значения углов: определим предварительные координаты точек 3 и 4 по ходу 1-2-3-4-1-2 и выполним предварительное уравнивание координат (табл. 4.61); по полученным данным из решения обратной геодезической задачи найдем дирекционные углы определяемых сторон сети.
Таблица 4.61
№№ точек |
Дирекц.углы α |
Рассто-яния s , м |
Приращения координат, м |
Координаты, м |
№№ точек |
||
Δх |
Δу |
Х |
Y |
||||
1 |
|
|
|
|
|
|
|
23°15'25,4" |
|
|
|
||||
2 |
8836,421 |
5748,265 |
2 |
||||
128°25'15,5" |
4679,799 |
-2908,189 |
+3666,464 |
||||
3 |
5928,232 |
9414,729 |
3 |
||||
202°47'53,0" |
6284,090 |
-5793,154 |
-2434,986 |
||||
4 |
135,078 |
6979,743 |
4 |
||||
332°29'25,5" |
5896,343 |
+5229,665 |
-2723,503 |
||||
1
|
5364,743 5364,756 |
4256,240 4256,214 |
1 1(исх) |
||||
|
|
|
|
||||
|
|
|
|
||||
Пользуясь табл. 4.61, вычислим по формулам (4.203) значения коэффициентов уравнений поправок (табл. 4.62).
Таблица 4.62
Значения коэффициентов уравнений поправок
Направление |
a |
b |
1-3 |
+3,951 |
-0,432 |
2-3 |
+3,453 |
+2,739 |
3-4 |
-1,272 |
+3,026 |
1-4 |
+1,616 |
+3,103 |
Вычислим по формуле (4.205) значения ориентирующих углов в пунктах:
Значения свободных членов находим по формуле (16.195) – табл. 4.63.
Таблица 4.63
Таблица свободных членов
Пункт 1 |
l |
Пункт 2 |
l |
Пункт 3 |
l |
Пункт 4 |
l |
1-2 |
+0,09 |
2-1 |
-0,27 |
3-1 |
+0,45 |
4-1 |
-0,43 |
1-3 |
-0,28 |
2-3 |
+0,27 |
3-2 |
+0,16 |
4-3 |
+0,42 |
1-4 |
+0,20 |
|
|
3-4 |
-0,62 |
|
|
|
+0,01 |
|
0 |
|
-0,01 |
|
-0,01 |
Незначительные отступления от условия (4.208) объясняются погрешностями округлений.
После подстановки значений коэффициентов a и b и свободных членов l в уравнения (4.219) с учетом преобразований значений свободных членов при объединениях уравнений по правилам Шрейбера получим:
1.
2.
3.
4.
(4.221)
5.
6.
7.
8.
Приведем уравнения 5, 6, 7 и 8 системы (4.221) к весам, равным «минус единице». Для этого умножим коэффициенты и свободные члены этих уравнений на . Получим
1.
2.
3.
4. (4.222)
5.
6.
7.
8.
Составим по уравнениям (4.222) матрицу коэффициентов, свободных членов и весов для получения нормальных уравнений поправок (табл. 4.64).
Таблица 4.64
Ведомость коэффициентов уравнений поправок, свободных членов и весов
|
1(ξ3) |
2(η3) |
3(ξ4) |
4(η4) |
l |
p |
1 |
-3,951 |
0,432 |
|
|
0,085 |
1 |
2 |
|
|
-1,616 |
-3,103 |
-0,115 |
1 |
3 |
-3,453 |
-2,739 |
|
|
0,215 |
1 |
4 |
-1,272 |
3,026 |
1,272 |
-3,026 |
-0,100 |
1 |
5 |
-1,613 |
0,176 |
-0,660 |
-1,267 |
0 |
-1 |
6 |
-1,727 |
-1,370 |
|
|
0 |
-1 |
7 |
-3,542 |
0,294 |
0,519 |
-1,235 |
0 |
-1 |
8 |
-0,172 |
-3,065 |
-0,636 |
1,513 |
0 |
-1 |
В соответствии с правилами составления нормальных уравнений получим:
1.
2.
3.
(4.223)
4.
Из решения системы уравнений (4.223) значения поправок равны:
Полученные поправки следует ввести в значения предварительных координат пунктов 3 и 4 (табл. 4.61).
Вычисляем
поправки (в секундах) в направления:
;
;
;
.
Используя первоначальные формулы поправок (4.217), определим поправки (в секундах) в направления и в измеренные углы:
(невязка
= +1,2)
(невязка
= -2,4)
Убеждаемся, что поправки вычислены правильно. Небольшое несоответствие в величинах практических невязок и сумм поправок вполне объясняется погрешностями округлений.
Предлагаем самостоятельно закончить дальнейшую обработку уравнивания с выполнением необходимых контрольных вычислений.