4.6.4. Уравнивание системы полигонометрических ходов с одной узловой точкой

На местности между исходными линиями АВ, CD, FE проложена система полигонометрических ходов (рис. 4.10) с одной узловой точкой М: В-N-M; D-1-M; F-3-2-M. На схеме указано направление движения в полигонометрических ходах.

Координаты исходных пунктов В, D и F приведены в табл. 4.18, значения исходных дирекционных углов – в табл. 4.19, измеренных горизонтальных углов и расстояний – в табл. 4.20.

Средняя квадратическая погрешность измерения горизонтальных углов m_β = 2,0" (измерения углов равноточные). Относительная погрешность измерения расстояний составила m_s(отн) 1:120000. Используя формулу

, (4.159)

получим абсолютные средние квадратические погрешности измерения линий: m_s1 = =21 мм; m_s2 = 25 мм; m_s3 = 16 мм; m_s4 = 21 мм; m_s5 = 14 мм; m_s6 = 17 мм; m_s7 = 13 мм.

Значения весов p_i и обратных весов q_i измеренных величин в соответствии с принятой их нумерацией приведены в табл. 4.21. Значения весов получены по формулам (3.5).

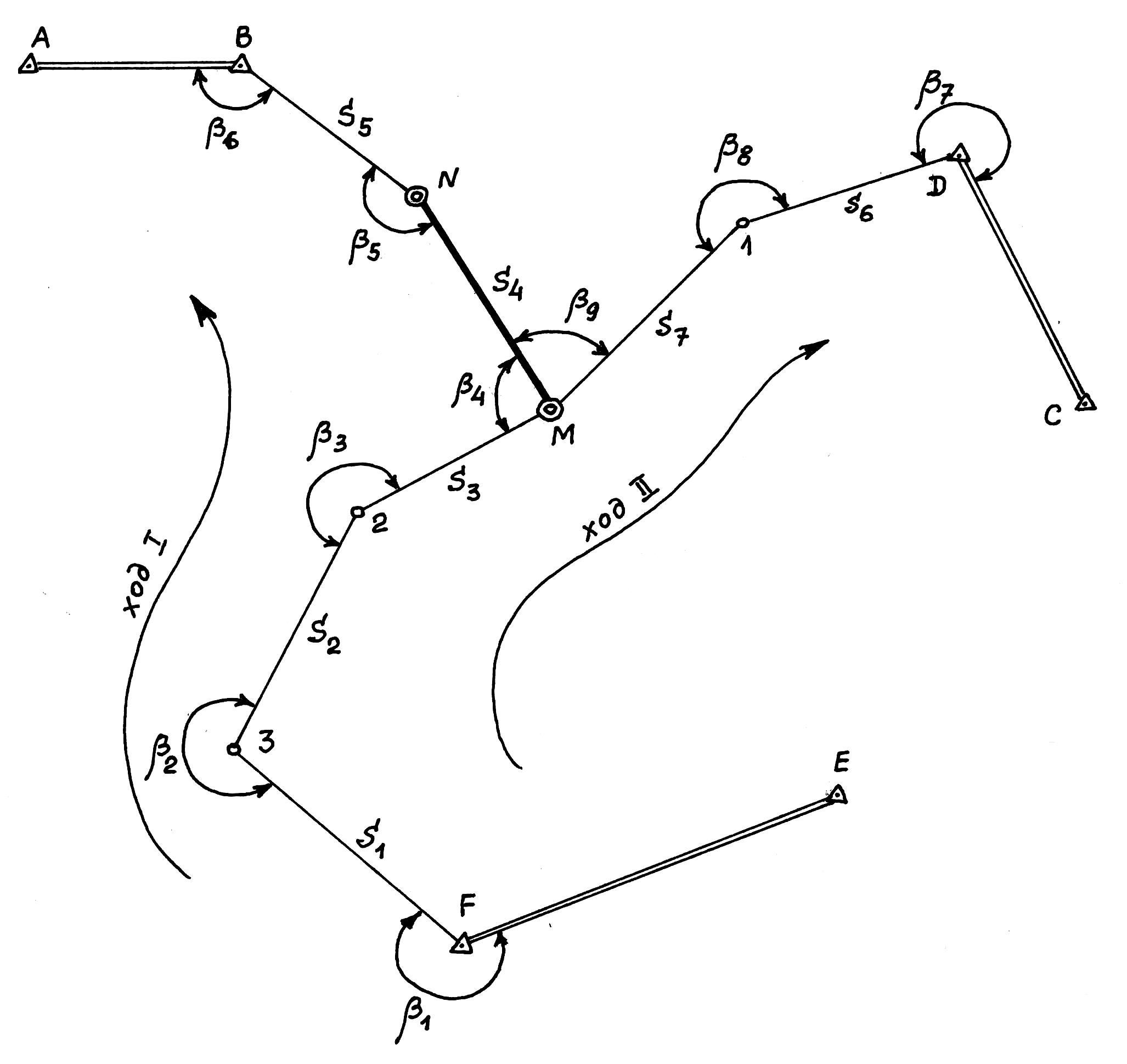
Рис. 4.10. Схема полигонометрических ходов с одной узловой точкой

Таблица 4.18

Координаты исходных пунктов

Пункт	X, м	Y, м
В	8716,883	896,751
D	8941,804	6805,567
F	1207,063	3320,677

Таблица 4.19

Значения исходных дирекционных углов

Линия	α	Значение угла	α	Значение угла
АВ	α АВ	89о31' 14,7''	α BA	269 о31' 14,7''
CD	α CD	327 о04' 59,2''	α DC	147 о04' 59,2''
EF	α EF	243 о25' 05,9''	α FE	63 о25' 05,9''

Таблица 4.20

Значения измеренных углов и расстояний

№№ точек	β i	Значение угла	si	Значение расстояния, м
F	β 1	249 о13' 24,8''	s1	2493,846
3	β 2	253 о06' 07,7''	s2	3004,255
2	β 3	214 о25' 11,4''	s3	1875,063
M	β 4	69 о36' 08,8''	s4	2500,681
N	β 5	160 о14' 00,5''	s5	1701,242
B	β 6	159 о31' 10,3''
M	β 9	77 о42'13,6''	s7	1505,218
1	β 8	210 о13' 16,4''	s6	2003,754
D	β 7	269 о23' 24,8''

Таблица 4.21

Значения весов и обратных весов измеренных величин

№ измеренной величины	Обозначение измеренной величины	Вес pi	Обратный вес qi
1	β 1	1	1
2	β 2	1	1
3	β 3	1	1
4	β 4	1	1
5	β 5	1	1
6	β 6	1	1
7	β 7	1	1
8	β 8	1	1
9	β 9	1	1
10	s1	0,907	1,102
11	s2	0,640	1,562
12	s3	1,563	0,640
13	s4	0,907	1,102
14	s5	2,041	0,490
15	s6	1,384	0,722
16	s7	2,367	0,422

Требуется найти уравненные значения координат точек 1, 2, 3, N, узловой точки М и уравненное значение дирекционного угла линии MN.

Решение.

В каждом из полигонометрических ходов (ход (1) : F-3-2-M-N-B; ход (2): F-3-2-M-1-D), как и в примере 4.6.3, возникает по три условия: одно – для дирекционных углов; два – абсцисс и ординат.

Выполним предварительные вычисления в полигонометрических ходах (табл. 4.22).

Шаг 1. Общее число измерений n = 16, число необходимых измерений k = =10, число избыточных измерений r = 6.

Шаг 2. Составим условные уравнения для ходов (1) и (2):

- условие дирекционных углов:

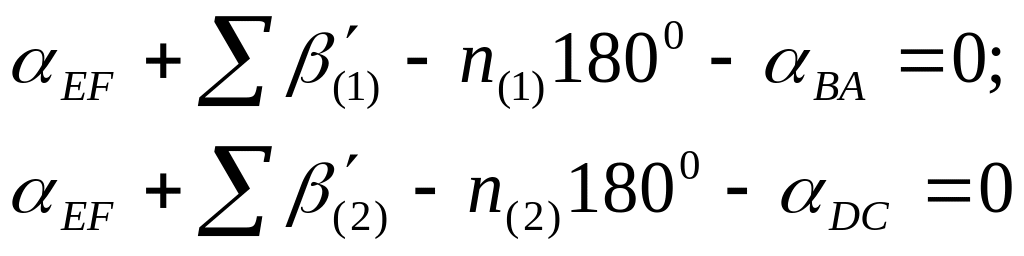(4.160)

- условие координат (для абсцисс):

(4.161)

- условие координат (для ординат):

(4.162)

Шаг 3. Приведем условные уравнения к линейному виду (подробные пояснения даны в примере 4.6.3). Получим условные уравнения поправок вида:

Таблица 4.22

Предварительные вычисления в системе полигонометрических ходов с одной узловой точкой

№№ точек	Гориз.углы β	Дирекц.углы α	Рассто-яния s , м	Приращения координат, м		Координаты, м		№№ точек
				Δx	Δy	X	Y
E				Ход (1)
		243о 25' 05,9"
F	249 о 13' 24,8''					1207,083	3320,677	F
		312о 38' 30,7"	2493,846	+1689,365	-1834,479
3	253 о 06' 07,7''					2806,448	1486,198	3
		25о 44' 38,4"	3004,255	+2706,064	+1304,901
2	214 о 25' 11,4''					5602,512	2791,099	2
		60о 09' 49,8"	1875,063	+932,884	+1626,526
M	69 о 36' 08,8''					6535,396	4417,625	M
		309о 45' 58,6"	2500,681	+1599,579	-1922,174
N	160 о 14' 00,5''					8134,975	2495,451	N
		289о 59' 59,1"	1701,242	+581,852	-1598,647
B	159 о 31' 10,3''					8716,827	896,804	Bo
		269о 31' 09,4" (269о 31' 14,7")
A						8716,883	896,751	В
				Ход (2)
E
		243о 25' 05,9"
F	253 о 06' 07,7''					1207,083	3320,677	F
		312о 38' 30,7"	2493,846	+1689,365	-1834,479
3	214 о 25' 11,4''					2806,448	1486,198	3
		25о 44' 38,4"	3004,255	+2706,064	+1304,901
2	69 о 36' 08,8''					5602,512	2791,099	2
		60о 09' 49,8"	1875,063	+932,884	+1626,526
M	147о 18' 22,4''					6535,396	4417,625	M
		27о 28' 12,2"	1505,218	+1335,508	+694,334
1	207 о 28' 12,2''					7870,904	5111,959	1
		57о 41' 28,6"	2003,754	+1070,968	+1693,534
D	269 о 23' 24,8''					8941,872 8941,804	6805,493 6805,567	Do D
		147о 04' 53,4" (147о04'59,2")
C

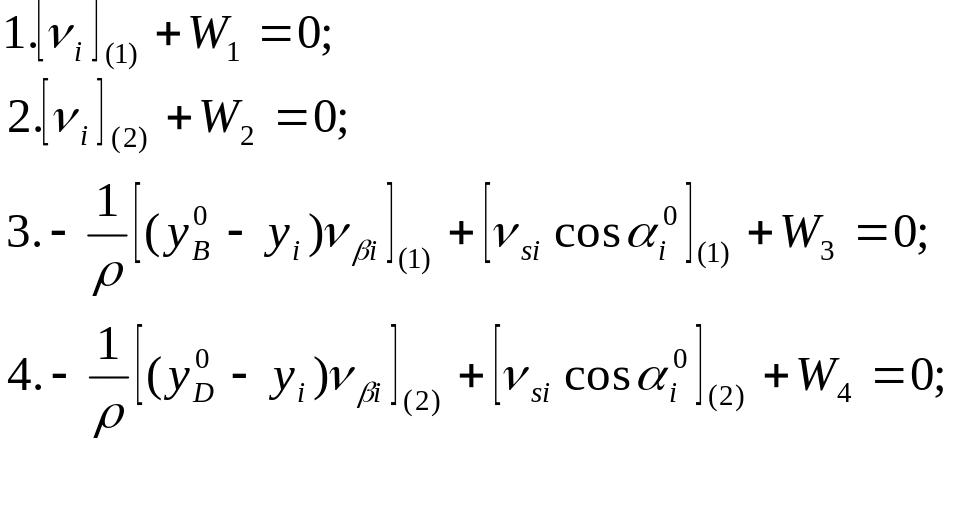(4.163)

Вычислим значения невязок (свободных членов уравнений). Для этого подставим в формулы (4.160) – (4.162) значения измеренных величин, а также результаты предварительных вычислений. Получим:

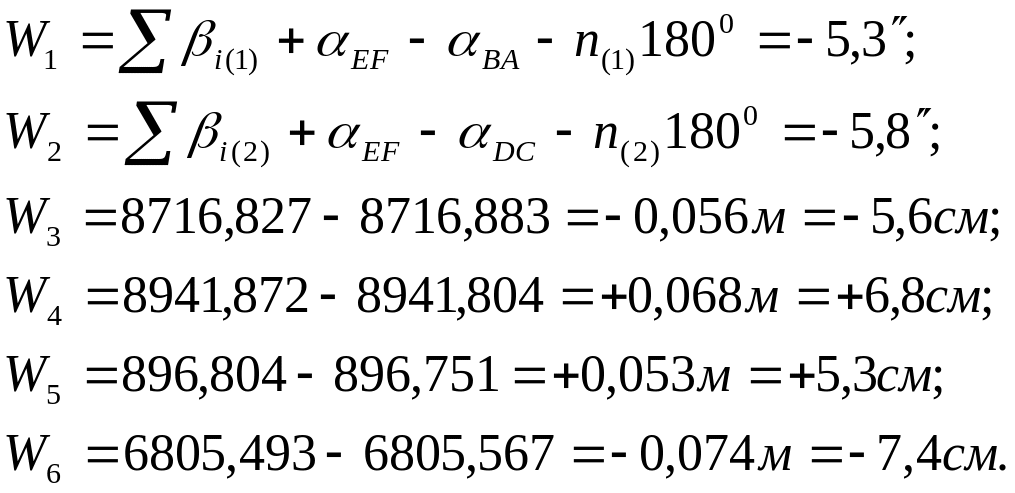(4.164)

Здесь n₍₁₎ = 6, n₍₂₎ = 6 (с учетом суммирования углов в точке поворота М).

Приведем уравнения поправок в развернутом виде:

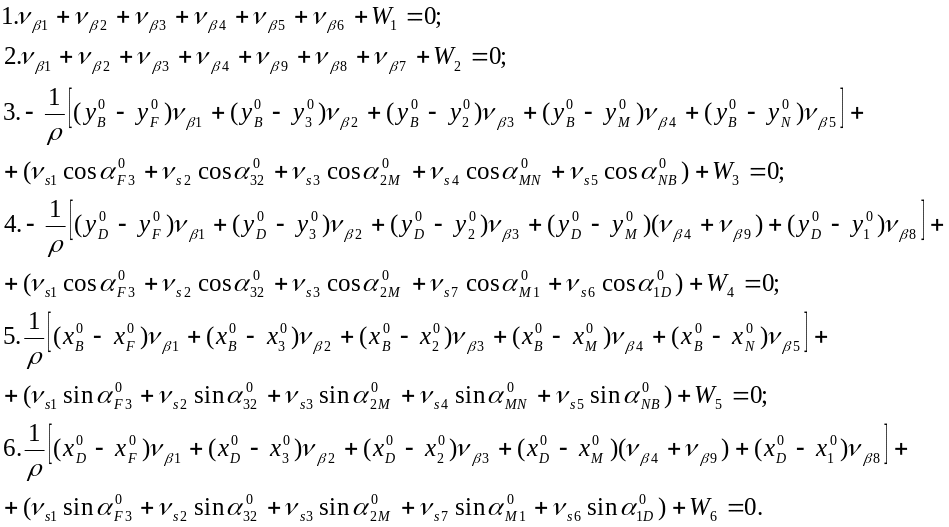(4.165)

Составим по данным табл. 4.22 таблицу значений sin и cos дирекционных углов и разностей координат (x_n^o – x_i^o) и (y_n^o – y_i^o), необходимых для определения коэффициентов уравнений поправок.

Составим окончательные выражения уравнений поправок с учетом данных табл. 4.23 и значений свободных членов:

Таблица 4.23

Значения разностей координат (км) и функций sin и cos дирекционных углов

№№ точек	Значение дирекционного угла		км	км
F
	312о 38' 30,7''	+0,6774	+7,5097	-2,4239
3		-0,7356
	25 о 44' 38,4''	+0,9007	+5,8204	-0,5894
2		+0,4344
	60 о09'49,8''	+0,4975	+3,1143	-1,8943
M		+0,8675
	309 о45' 58,6''	+0,6397	+2,1814	-3,5208
N		-0,7687
	289 о59' 59,1''	+0,3420	+0,5819	-1,5986
B		-0,9397
F
	312 о 38' 30,7''	+0,6774	+7,7348	+3,4848
3		-0,7356
	25 о 44' 38,4''	+0,9007	+6,0454	+5,3193
2		+0,4344
	60 о 09' 49,8''	+0,4975	+3,3394	+4,0144
M		+0,8675
	27 о 28' 12,2''	+0,8873	+2,4065	+2,3878
1		+0,4613
	57 о 41' 28,6''	+0,5345	+1,0710	+1,6935
D		+0,8452

(4.166)

Составим матрицу (таблицу) коэффициентов и обратных весов уравнений поправок (табл. 4.24).

Таблица 4.24

Значения коэффициентов уравнений поправок и обратных весов измеренных величин

i→ j↓	1 β1	2 β2	3 β3	4 β4	5 β5	6 β6	7 β7	8 β8	9 β9
1	1	1	1	1	1	1	0	0	0
2	1	1	1	1	0	0	1	1	1
3	+1,1752	+0,2857	+0,9184	+1,7069	+0,7750	0	0	0	0
4	-1,6895	-2,5788	-1,9462	-1,1576	0	0	0	-0,8210	-1,1576
5	+3,6408	+2,8218	+1,5098	+1,0576	+0,2821	0	0	0	0
6	+3,7499	+2,9309	+1,6190	+1,1667	0	0	0	+0,5192	+1,1667
qi	1	1	1	1	1	1	1	1	1

Таблица 4.24 (продолжение)

i→ j↓	10 s1	11 s2	12 s3	13 s4	14 s5	15 s6	16 s7
1	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0
3	0,6774	0,9007	0,4975	0,6397	0,3420	0	0
4	0,6774	0,9007	0,4975	0	0	0,5345	0,8873
5	-0,7356	0,4344	0,8675	-0,7687	-0,9397	0	0
6	-0,7356	0,4344	0,8675	0	0	0,8452	0,4613
qi	1,102	1,562	0,640	1,102	0,490	0,722	0,422

Шаг 4. Составим и решим нормальные уравнения коррелат. Принцип составления нормальных уравнений коррелат приведен в разделе 4.2, способ решения системы линейных уравнений приведен в разделе 4.4.

1. 6k₁ + 4 k₂ + 4,8611 k₃ – 7,3721 k₄ + 9,3121 k₅ + 9,4665 k₆ – 5,3 = 0;

2. 4 k₁ + 7 k₂ + 4,0861 k₃ – 9,3507 k₄ + 9,0300 k₅ + 11,1494 k₆ – 5,8 = 0;

3. 4,8611 k₁ + 4,0861 k₂ + 8,2596 k₃ – 4,5541 k₄ + 8,1330 k₅ + 9,0604 k₆ – 5,6 = 0;

4. -7,3721 k₁ – 9,3507 k₂ – 4,5541 k₃ + 19,1162 k₄ – 17,2466 k₅ – 19,3348 k₆ + 6,8 = 0;

5. 9,3121 k₁ + 9,0300 k₂ + 8,1330 k₃ – 17,2466 k₄ + 27,1521 k₅ + 26,9740 k₆ + 5,3 = 0;

6. 9,4665 k₁ + 11,1494 k₂ + 9,0604 k₃ – 19,3348 k₄ + 26,9740 k₅ + 30,2433 k₆ – 7,4 = 0.

(4.167)

Из решения системы линейных уравнений получаем:

k₁ = +2,5830; k₂ = -0,9683; k₃ = -0,1358; k₄ = -0,0966; k₅ = -4,8556; k₆ = +4,1088.

Контрольная подстановка в исходные уравнения (4.167) показывает выполнение указанных условий.

Шаг 5. Вычисление значений поправок в измеренные величины.

В соответствии с правилами составления уравнений поправок для их вычисления получим:

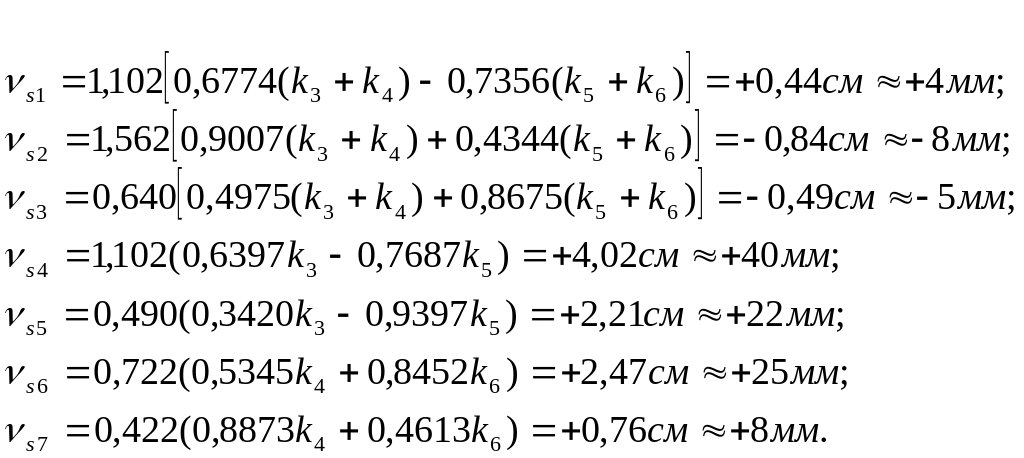
Контрольная подстановка полученных значений поправок в исходные уравнения (4.166) показала выполнение указанных условий.

Шаг 6. Вычисление уравненных значений углов и расстояний и вычисление уравненных значений координат точек и дирекционного угла узловой линии.

Здесь не будем приводить отдельно значения уравненных углов и расстояний, а запишем их величины непосредственно в таблицу уравнивания (табл. 4.25), по форме идентичную таблице предварительных вычислений (табл. 4.22).

Таблица 4.25

Контрольные вычисления в системе полигонометрических ходов с одной узловой точкой

№№ точек	Гориз.углы β	Дирекц.углы α	Рассто-яния s , м	Приращения координат, м		Координаты, м		№№ точек
				Δx	Δy	X	Y
E				Ход (1)
		243о 25' 05,9"
F	249 о 13' 24,1''					1207,083	3320,677	F
		312о 38' 30,0"	2493,850	+1689,362	-1834,488
3	253 о 06' 07,9''					2806,445	1486,189	3
		25о 44' 37,9"	3004,247	+2706,060	+1304,891
2	214 о 25' 12,4''					5602,505	2791,080	2
		60о 09' 50,3"	1875,058	+932,878	+1626,524
M	69 о 36' 09,9''					6535,383	4417,604	M
		309о 46' 00,2"	2500,721	+1599,620	-1922,192
N	160 о 14' 01,6''					8135,003	2495,412	N
		290о 00' 01,8"	1701,264	+581,881	-1598,660
B	159 о 31' 12,9''					8716,884	896,752	Bo
		269о 31' 14,7" (269о 31' 14,7")
A						8716,883	896,751	В
				Ход (2)
E
		243о 25' 05,9"
F	249 о 13' 24,1''					1207,083	3320,677	F
		312о 38' 30,0"	2493,850	+1689,362	-1834,488
3	253 о 06' 07,9''					2806,445	1486,189	3
		25о 44' 37,9"	3004,247	+2706,060	+1304,891
2	214 о 25' 12,4''					5602,505	2791,080	2
		60о 09' 50,3"	1875,058	+932,878	+1626,524
M	147о 18' 27,5''					6535,383	4417,604	M
		27о 28' 17,8"	1505,243	+1335,511	+694,382
1	210 о 13' 17,6''					7870,894	5111,986	1
		57о 41' 35,4"	2003,762	+1070,921	+1693,583
D	269 о 23' 23,8''					8941,815 8941,804	6805,569 6805,567	Do D
		147о 04' 59,2" (147о04'59,2")
C

Как видно из табл. 4.25 и результатов проверки правильности вычисления поправок в измеренные углы, остаточных невязок в уравнениях, составленных по условиям дирекционных углов, нет. Остаточные невязки в координатах: W₃= 8716,884 – 8716,883 = + 1 мм; W₄ = 896,752 – 896,751 = + 1 мм; W₅ = 8941,815 –

-8941,804 = = + 11 мм; W₆ = 6805,569 – 6805,567 = + 2 мм, что является вполне удовлетворительным. Небольшие отступления здесь определяются только ошибками округлений.

Задача решена!