2.5.1. Метод наименьших квадратов

Метод наименьших квадратов предложен в 1806 г. французским математиком Лежандром для решения неопределенных систем линейных уравнений.

Метод наименьших квадратов – это метод нахождения оптимальных параметров линейной регрессии, таких, что сумма квадратов отклонений (регрессионных остатков) минимальна для исследуемого набора сопоставляемых статистических данных. Другими словами, идея метода наименьших квадратов заключается в минимизации суммы квадратов расстояний по оси ординат между измеренными значениями y_i и вычисленными значениями y_i' с использованием полученной линии регрессии

y_i' = ax_i + b. (2.66)

Таким образом, уравнение регрессии (2.66) составляют при соблюдении условия

. (2.67)

Часто знак суммы заменяют на знак суммы […] веденный К.Гауссом. В связи с этим выражение (2.67) можно записать в виде

[ ] → min . (2.68)

2.5.2. Линейная регрессия

Значения коэффициентов а и b в уравнении (2.66) могут быть найдены из решения системы линейных уравнений вида (1.79)

(2.69)

Из (2.69) следует, что

; . (2.70)

Рассмотрим пример вычисления коэффициентов а и b и оценки их доверительных интервалов по методу наименьших квадратов.

Пример 2.14. В разное время в течение х часов сейсмическая станция, установленная в горной выработке, зарегистрировала у сигналов (см. табл. 2.11). Установить зависимость числа зарегистрированных сигналов от времени их регистрации.

Примечание: таблица 2.11 составлена с учетом вычисления коэффициента корреляции между величинами х и у.

Таблица 2.11

К примеру 2.14

№№ пп	х	у	х2	ху	(х – хо)	(х – хо)2	(у – уо)	(у – уо)2	(х – хо)х х(у – уо)
1	5	1	25	5	-3	9	-14	196	+42
2	6	3	36	18	-2	4	-12	144	+24
3	6	8	36	48	-2	4	-7	49	+14
4	7	6	49	43	-1	1	-9	81	+9
5	7	14	49	98	-1	1	-1	1	+1
6	7	13	49	91	-1	1	-2	4	+2
7	8	12	64	96	0	0	-3	9	0
8	8	20	64	160	0	0	+5	25	0
9	8	15	64	120	0	0	0	0	0
10	8	17	64	136	0	0	+2	4	0
11	9	26	81	234	+1	1	+11	121	+11
12	9	22	81	198	+1	1	+7	49	+7
13	10	21	100	210	+2	4	+6	36	+12
14	10	20	100	200	+2	4	+5	25	+10
15	12	27	144	324	+4	16	+12	144	+48
	120	225	1006	1980	0	46	0	888	+179
	хо 8	уо 15

Решение.

В предпоследней строке таблицы выделены жирным шрифтом суммы по соответствующим столбцам.

По формулам (2.70) находим значения коэффициентов уравнения (2.66):

; .

Таким образом, уравнение регрессии будет иметь вид: у = 3,913х – 16,304.

Оценка коэффициента а может быть выполнена и другим способом:

, (2.71)

где ρ_х,у – коэффициент корреляции, определяемый по формуле (2.53); σ_х и σ_у – стандарты переменных х и у, вычисляемые по формуле (2.5) или (2.6).

Получим: ; ; .

Отсюда , что сравнительно близко к значению, полученному ранее. Расхождения объясняются небольшим объемом выборки (n = 15).

Составим таблицу разностей (2.68).

Таблица 2.12

Сопоставление значений у с линией регрессии

х	5	6	6	7	7	7	8	8	8	8	9	9	10	10	12
у	1	3	8	6	14	13	12	20	15	17	26	22	21	20	27
у'	3,3	7,2	7,2	11,1	11,1	11,1	15,0	15,0	15,0	15,0	18,9	18,9	22,8	22,8	30,7
Δу	-2,3	-4,2	+0,8	-5,1	+2,9	+1,9	-3,0	+5,0	0,0	+2,0	+7,1	+3,1	-1,8	-2,8	-3,7
(Δу)2	5,3	17,6	0,6	26,0	8,4	3,6	9,0	25,0	0,0	4,0	50,4	9,6	3,2	7,8	13,7

Сумма Δу = -0,1. Сумма (Δу)² = 184,2.

Среднюю квадратическую погрешность разностей определяют по формуле

. (2.72)

По формуле (2.72) получим .

Средние квадратические погрешности коэффициентов а и b, m_a и m_b, оценивают по формулам:

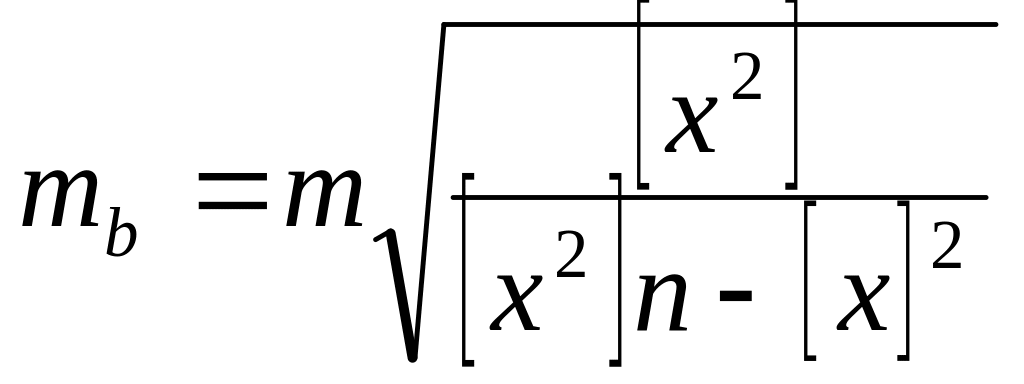; . (2.73)

Таким образом, получим:

; .

Если установить доверительную вероятность 0,95 (уровень значимости 0,05), то для числа степеней свободы ν = (n – 2) = 15 - 2 = 13 по таблице приложения 10 найдем значение t = 2,16, что позволит установить доверительные интервалы для вычисленных коэффициентов a и b: Δ_а = tm_a = 2,16∙0,554 = 1,197; Δ_b = tm_b = 2,16∙4,54 = 9,806.