1.6.4. Распределение Стьюдента
Распределение Стьюдента используется часто при интервальных оцениваниях параметров, т.е. при вероятностном определении ширины интервала, в котором может находиться данная случайная величина. Кроме того, указанное распределение используют и при проверке статистических гипотез. Распределение Стьюдента называют еще t-распределением.
Плотность вероятности случайной величины Х, которая имеет t-распределение, определяется выражением:
,
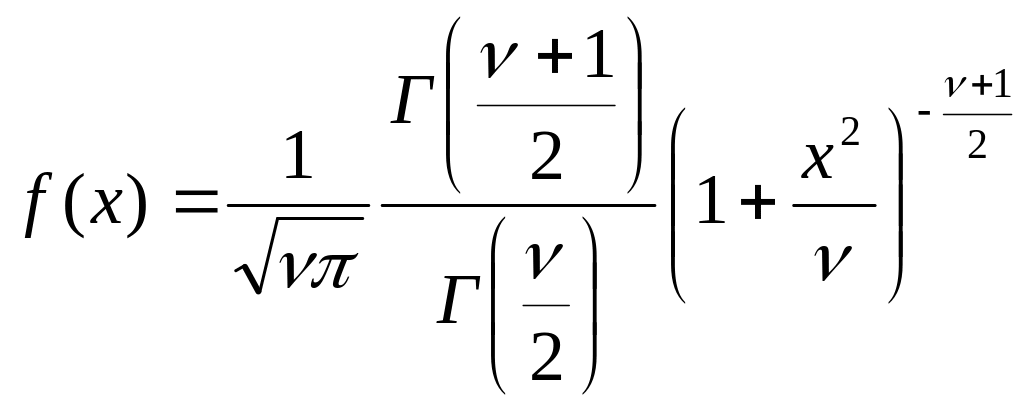(1.116)
где ν – параметр, определяющий число степеней свободы; Г – гамма-функция Эйлера, определяемая выражением вида:
.
(1.117)
Распределение Стьюдента симметричное. При этом математическое ожидание, медиана и мода распределения равны друг другу и равны нулю. Поскольку распределение симметричное, то и значение асимметрии также равно нулю.
Дисперсия
(при ν
≥
2), эксцесс
(при ν
≥
4).
График распределения Стьюдента показан на рис. 1.13.
В приложении 2 приведены значения вероятностей для установленных значений t, определяемых для симметричного диапазона ±Δ относительно стандартного отклонения :
.
(1.118)
Рис. 1.13. Распределение Стьюдента
Для
гамма-функции математическое ожидание
М(Х)
= ν,
мода МО
= ν
– 2 (при ν
≥ 2), дисперсия D
= 2
ν,
асимметрия А
=
,
эксцесс Е
=
.
В приложении 3 для удобства в вычислениях приведены значения гамма-функции Эйлера.
Пример 1.20. Определить вероятность того, что при повторном испытании (опробовании) отклонение результата от среднего арифметического его значения составит 46 единиц. Стандартное отклонение при обработке вариационного ряда составило 68 единиц.
Решение.
Поскольку Δ = 46, а = 68, то t = 46/68 = 0,676.
Для t = 0,676 по таблице приложения 2 интерполированием находим, что р = 0,5005 (практически – 0,5 или 50%).
1.6.5. Распределение Шарлье
Как было указано выше (п. 1.6.3), нормальное распределение, плотность вероятностей случайной величины которого описывается выражением (1.111), является симметричным распределением. На практике же симметричные распределения встречаются крайне редко, более всего они имеют ту или иную асимметрию. Если асимметрия распределения окажется не очень большой, то такое распределение может быть выровнено с помощью закона Шарлье, в котором, кроме асимметрии, учитывается также и эксцесс. Плотность вероятности закона Шарлье представляется в виде:
,
(1.119)
где f(x) – плотность нормального закона распределения; F(t) – интегральная функция распределения (1.113), в которой t определяется соотношением (1.112); А – асимметрия; Е – эксцесс.
Второе слагаемое является поправкой к нормальному закону распределения с учетом асимметрии и эксцесса исследуемого распределения. Если асимметрия и эксцесс будут равны нулю, то распределение (1.119) примет вид нормального распределения.
Указанное распределение можно записать в виде
,
(1.120)
где h – ширина классового интервала интервального вариационного ряда.
Рассмотрим применение закона Шарлье для выравнивания опытного распределения.
Пример 1.21. Выполнить выравнивание распределения содержания для интервального вариационного ряда, представленного в табл. 1.4, используя закон Шарлье.
Решение.
Предварительно
составим таблицу интервального
вариационного ряда, введя новую переменную
Х =
.
Таблица 1.22
Нормирование интервального вариационного ряда (табл. 1.4)
С, г/м3 |
122 |
239 |
356 |
473 |
590 |
707 |
824 |
Х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
r |
0,20 |
0,28 |
0,19 |
0,14 |
0,10 |
0,05 |
0,05 |
Составим основную расчетную таблицу.
Таблица 1.23
Расчетная таблица
Х |
r |
rX |
rX2 |
rX3 |
rX4 |
1 |
0,20 |
0,20 |
0,20 |
0,20 |
0,20 |
2 |
0,28 |
0,56 |
1,12 |
2,24 |
4,48 |
3 |
0,19 |
0,57 |
1,71 |
5,13 |
15,39 |
4 |
0,14 |
0,56 |
2,24 |
8,96 |
35,84 |
5 |
0,10 |
0,50 |
2,50 |
12,50 |
62,50 |
6 |
0,05 |
0,30 |
1,80 |
10,80 |
64,80 |
7 |
0,05 |
0,35 |
2,45 |
17,15 |
120,05 |
α |
|
3,04 |
12,02 |
56,98 |
303,26 |
Математическое ожидание М(Х) = 3,04.
Математическое ожидание М(С) = 117 М(Х) + 5 = 117·3,04 +5 = 360,68 = 361 г/м3.
Дисперсия D(X) = rX2 – (rX)2 = 12,02 – 3,042 = 2,78. (X) = 1,67.
Дисперсия D (С) = 1172 · D (X) = 1172 · 2,78 = 38055. (С) = 195,08 = 195 г/м3.
=
56,98 – 3 · 3,04 · 12,02 + 2 · 3,043
= +3,55.
Асимметрия
= +3,55 / 1,673
= +0,76.
.
Эксцесс
20,67
/ 1,674
= 2,66 – 3 = -0,34.
Выразим переменную t с использованием формулы (1.112):
.
Далее запишем выражение (1.120) для относительной частоты (частости) распределения Шарлье:
rш
=
или rш
,
(1.121)
где
.
(1.122)
Составим таблицу для определения частостей, выровненных по закону Шарлье.
Таблица 1.24
№№ пп |
С |
r |
t |
F(x) |
S |
rш |
1 |
122 |
0,20 |
-1,226 |
0,187 |
1,186 |
0,13 |
2 |
239 |
0,28 |
-0,626 |
0,327 |
1,223 |
0,24 |
3 |
356 |
0,19 |
-0,026 |
0,399 |
1,052 |
0,25 |
4 |
473 |
0,14 |
0,574 |
0,339 |
0,817 |
0,17 |
5 |
590 |
0,10 |
1,174 |
0,201 |
0,705 |
0,08 |
6 |
707 |
0,05 |
1,774 |
0,083 |
0,950 |
0,05 |
7 |
824 |
0,05 |
2,374 |
0,024 |
1,827 |
0,03 |
|
|
1,01 |
|
|
|
0,95 |
Примечания:
1. Значения функции F(x) выбраны из таблицы приложения 6 по аргументу t.
2. Сумма rш теоретически должна быть равна 1, как, впрочем, и сумма r. Для интервального ряда отступление от единицы определяется только погрешностью округлений. Для распределения Шарлье отступление от 1 определяется тем, что пределы вычислений были ограничены значениями середин интервалов, теоретически же в данном распределении верхний предел равен бесконечности. Иногда выполняют выравнивание частостей, приводя их сумму к единице, разделив все значения на сумму частостей (в примере – на 0,95). Здесь и в дальнейшем выравнивание частостей производиться не будет.
Насколько эффективно выполнено выравнивание частостей покажут дальнейшие исследования с использованием специальных критериев (см. п. 1.7).