1.4.4. Огива

Если оси координат, в которых построена кумулята, поменять местами, то получится график, который называется огивой.

Огива также позволяет графически оценить величину медианы, а также проводить анализ распределения признака, аналогичный при использовании кумуляты.

На рис. 1.6 представлен график огивы, построенный для примера по данным табл. 1.14.

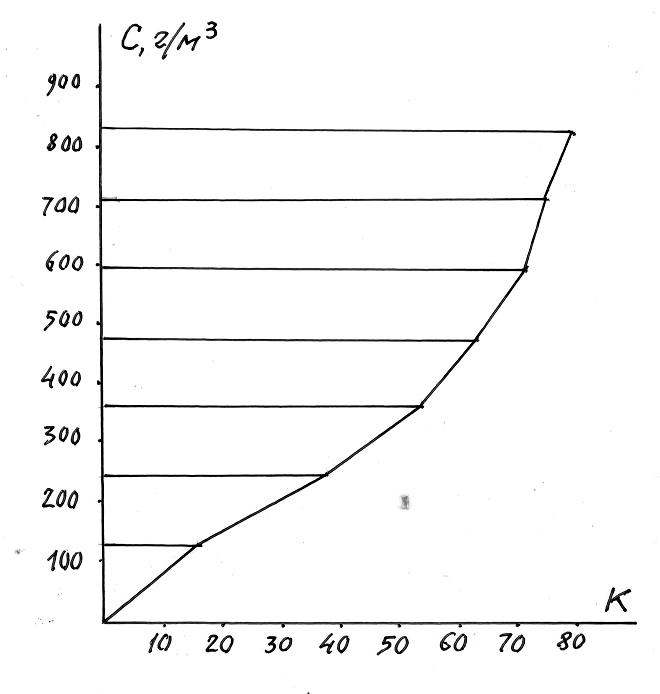
Рис. 1.6. Огива

1.5. Сглаживание эмпирических данных

Целью сглаживания эмпирических данных, представленных вариационными рядами, является получение непрерывных кривых распределения на основе полученных гистограмм, полигонов, кумулят и т.п., а также с привлечением к этим процедурам основных количественных и качественных характеристик: средних, асимметрии, эксцесса и др.

Следует иметь в виду, что полученная сглаживающая кривая может и не отражать фактический закон распределения, а являться некоторой математической моделью искомого распределения, более удобной для дальнейших исследований. Из курса «Геодезии» Вам известно, что, например, для описания фигуры Земли используется математическая модель, которая называется общим земным эллипсоидом, другой математической моделью, используемой на территории одного или нескольких государств, является референц-эллипсоид (в России – референц-эллипсоид Красовского). Вполне возможно, что при аппроксимации какого-либо распределения получится фрагмент, наиболее близкий к параболе, хотя, возможно, в природе и не существует параболических распределений случайных величин. Однако существуют, например, взаимосвязи между различными показателями, весьма близкие к параболическим.

Сглаживание может выполняться графически и аналитически.

Основным требованием при выполнении графического или аналитического сглаживания является подбор кривых такого математического вида и формы, для которых обеспечивается минимум отклонений Δ точек сглаживающих кривых от точек, например, полигона распределения в известных его ординатах:

[Δ²] min, (1.75)

где [...] – обозначение суммы.

1.5.1. Графическое сглаживание

Графическое сглаживание часто выполняется «на глаз» с последующим использованием сглаживающей функции для решения практических задач либо с использованием таблиц, построенных по сглаживающей функции через установленную дискретную величину.

Другим способом графического построения сглаживающей функции является способ «скользящей средней». При этом способе устанавливают ширину сглаживающего окна и при последующем (шаговом) перемещении этого интервала по графическому распределению вычисляют среднее значение признака в каждом шаге. Данный способ целесообразно использовать для непреобразованных вариационных рядов. Сам интервальный вариационный ряд практически и представляет собой такую же процедуру сглаживания. Тем более, что при использовании способа «скользящей средней» при сглаживании графически изображенных интервальных вариационных рядов шаг сглаживания должен быть сравнительно большим, иначе на каких-то двух последовательных шагах значение средней может и не измениться.

Сглаживающая плавная кривая чаще строится для полигонов распределений.

В качестве примера выполним графическое сглаживание полигонов распределений, изображенных на рис. 1.4 (см. рис. 1.7).

Как видно из рис. 1.7а, подбор сглаживающей кривой сравнительно легкий. В основной части полигона сглаживающая кривая практически проходит через его ординаты.

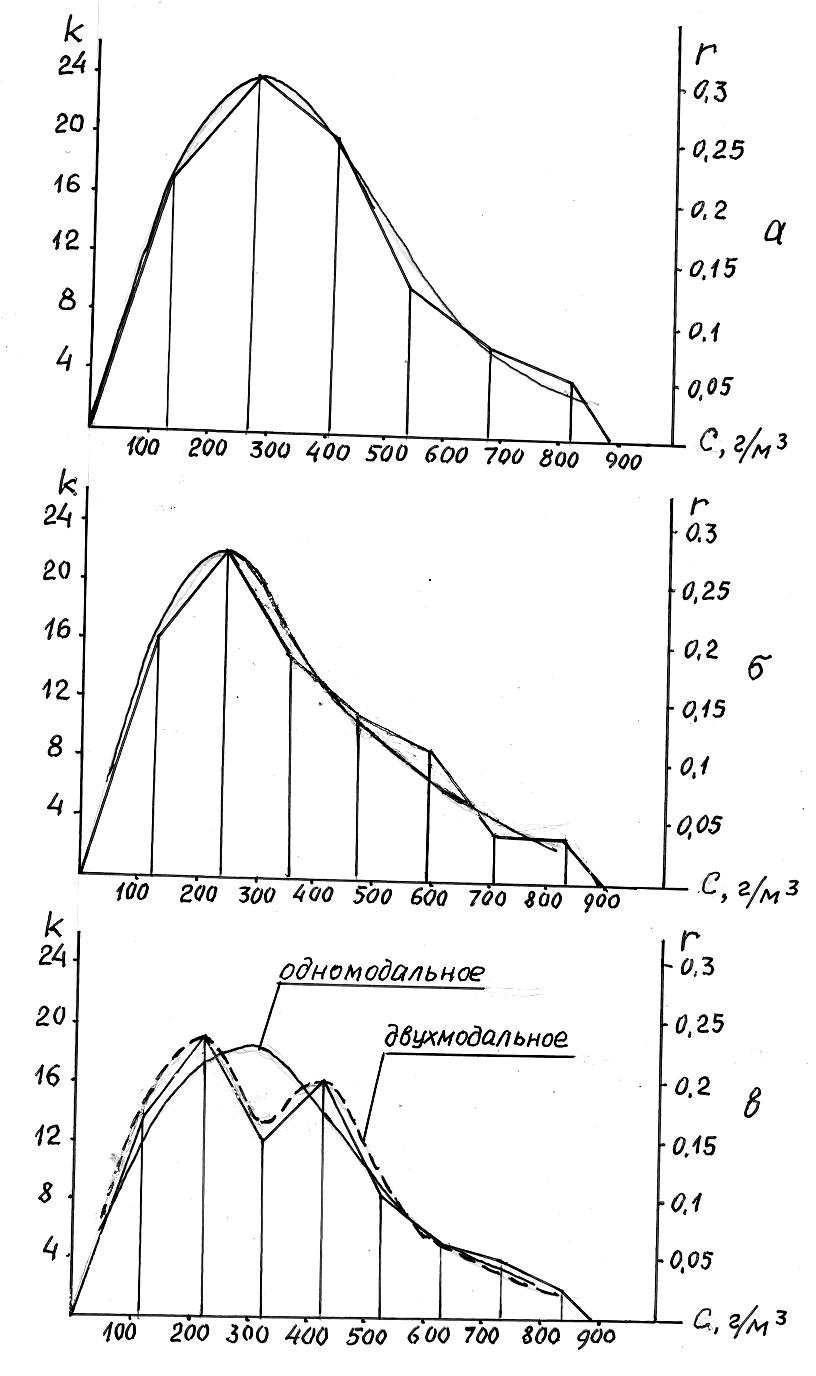
Рис. 1.7. Графическое сглаживание

а – табл. 1.3; б – табл. 1.4; в – табл. 1.5

Несколько отличаются расхождения сглаживающей кривой с полигоном для больших значений содержаний на рис. 1.7б. В данном случае недостаточность экспериментальных данных обусловила сравнительно большие вариации ординат на значениях от 500 до 900 г/м³. Это вызывает и увеличение контрольных сумм (1.75).

Полигон (рис. 1.7в) может быть сглажен довольно сложной кривой, определяющей двухмодальное распределение, если имеются основания считать, что данное распределение может быть отнесено к двухмодальным. Если же таких оснований нет, то сглаживающая кривая должна принять другой вид, соответствующий одномодальному распределению, несмотря на то, что показатель (1.75) качества сглаживания значительно увеличится.

Качество построения сглаживающей кривой оценим по условию (1.75). Для этого найдем разности

(1.76)

и вычислим сумму квадратов этих разностей (см. табл. 1.12).

Таблица 1.12

К оценке качества построения сглаживающей кривой

Инт. ряд	классы отклон.	1	2	3	4	5	6	7	8
Табл. 1.3	kСГЛ	17	24	19,5	10,5	6	3
	kФАКТ	17	24	20	9	6	4			80
	Δ	0,0	0,0	-0,5	+1,5	0,0	-1,0			0,0
	Δ2	0,0	0,0	0,25	2,25	0,0	1,0			3,5
Табл. 1.4	kСГЛ	17	22	16	10,5	6,5	4,5	3,5
	kФАКТ	16	22	15	11	8	4	4		80
	Δ	+1,0	0,0	+1,0	-0,5	-1,5	+0,5	-0,5		0,0
	Δ2	1,0	0,0	1,0	0,25	2,25	0,25	0,25		5,0
Табл. 1.5	kСГЛ	12	17	18	14	8,5	5	3,5	2
	kФАКТ	14	19	12	16	8	5	4	2	80
	Δ	-2,0	-2,0	+6,0	-2,0	+0,5	0,0	-0,5	0,0	0,0
	Δ2	4,0	4,0	36,0	4,0	0,25	0,0	0,25	0,0	48,5

Примечание: для данных табл. 1.5 оценка сглаживания выполнена для одномодального распределения.

Таблица 1.13

Таблица распределения содержания, представленная полигоном,

изображенным на рис. 1.7 б.

Содержание С, г/м3	Частость k	Содержание С, г/м3	Частость k	Содержание С, г/м3	Частость k
0	0,0
20	3,0	320	18,8	620	6,5
40	6,0	340	17,6	640	6,0
60	9,0	360	16,4	660	5,5
80	12,0	380	15,2	680	5,0
100	15,0	400	14,0	700	4,5
120	16,2	420	13,0	720	4,1
140	17,3	440	12,0	740	3,7
160	18,1	460	11,0	760	3,3
180	19,0	480	10,0	780	2,9
200	21,0	500	9,0	800	2,5
220	21,7	520	8,6	820	2,2
240	22,0	540	8,2	840	1,9
260	21,7	560	7,8	860	1,6
280	20,5	580	7,4	880	1,3
300	20,0	600	7.0	900	1,0
	252,5		175,2		52,0 479,7 ≈ 480

После выполнения графического сглаживания и оценки его качества для дальнейшей работы можно построить таблицу распределения с дискретностью, превышающей дискретность полигона распределения, для которого было выполнено сглаживание. Пример такой таблицы представлен для полигона, изображенного на рис. 1.7 б (см. табл. 1.13).

При пользовании таблицей такого вида следует иметь в виду, что показатель k определяет условную ожидаемую частоту появления данного значения признака при ограниченном числе измерений этого признака. Например, если при повторных измерениях на месторождении провести N = 14 разведочных линий с 10-ю разведочными скважинами на каждой (n = 14·10 = 140) по идентичной схеме разведки, то, например, следует ожидать, что значения содержания величиной С = 220 г/м³ получится в случаях (в 6 – 7-ми случаях). Это и определяет некоторую вероятность появления указанного события. Примерно так же можно оценить и появление содержания в каких-либо установленных пределах, например, в диапазоне 200 – 300 г/м³.

При выполнении графического сглаживания его полагают выполненным качественно, если площадь под сглаживающей кривой будет отличаться не более чем на 2-5% от площади полигона.

При значительных вариациях ординат полигона может получиться весьма сложная сглаживающая кривая. В таких случаях можно допустить вторичное сглаживание (сглаживание 2-го приближения). Однако 2-е приближение должно быть обосновано, поскольку вариации ординат могут быть вызваны и другими причинами, не связанными с недостаточностью эксперименатльных данных. В таких случаях следует остановиться на первом варианте сглаживания и составить таблицу, примерная форма которой представлена табл. 1.13.