1.4. Графическое изображение вариационных рядов

1.4.1. Гистограмма распределения

Гистограмма распределения строится для интервальных вариационных рядов в осях значений признака х и частот k (или относительных частот, частостей r). Часто одновременно указывают как оси частот, так и оси частостей. Ширину интервала в масштабе откладывают по оси х, при этом начало первого интервала соответствует х_{O1 min} = x_min, если в таблице интервального ряда с этого значения начинается первый интервал, как это принято, например, для интервальных рядов, приведенных в табл. 1.3, 1.4 и 1.5. Выше было указано, что первый интервал могут начинать и со значения х_min/2. В таких случаях при построении гистограммы учитывают данную рекомендацию. Центр интервала соответствует среднему значению признака в интервале (х_Oi).

На рис. 1.3 даны примеры построения гистограммы распределения для интервальных вариационных рядов, приведенных в табл. 1.3, 1.4 и 1.5.

1.4.2. Полигон распределения

Полигон распределения строят в тех же осях, что и гистограмму, но при этом значения k и r указывают для центра интервала. В левой часто полигона график начинают от нуля и соединяют со значением частоты или частости первого интервала, а в правой части показатель для среднего значения признака последнего интервала соединяют с максимальным значением варианта.

На рис. 1.4 приведены примеры построения полигона для интервальных вариационных рядов, приведенных в табл. 1.3, 1.4 и 1.5.

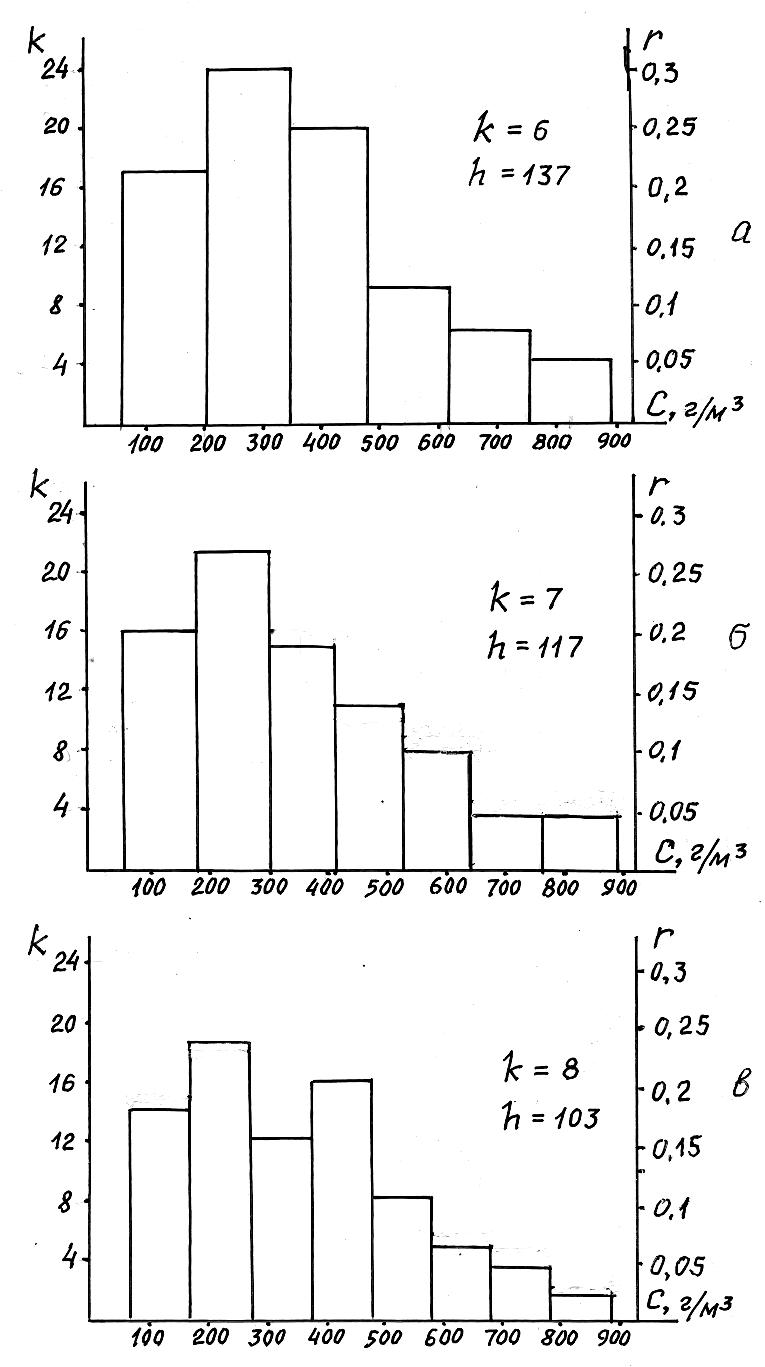
Рис. 1.3. Гистограмма

а – табл. 1.3; б – табл. 1.4; в – табл. 1.5

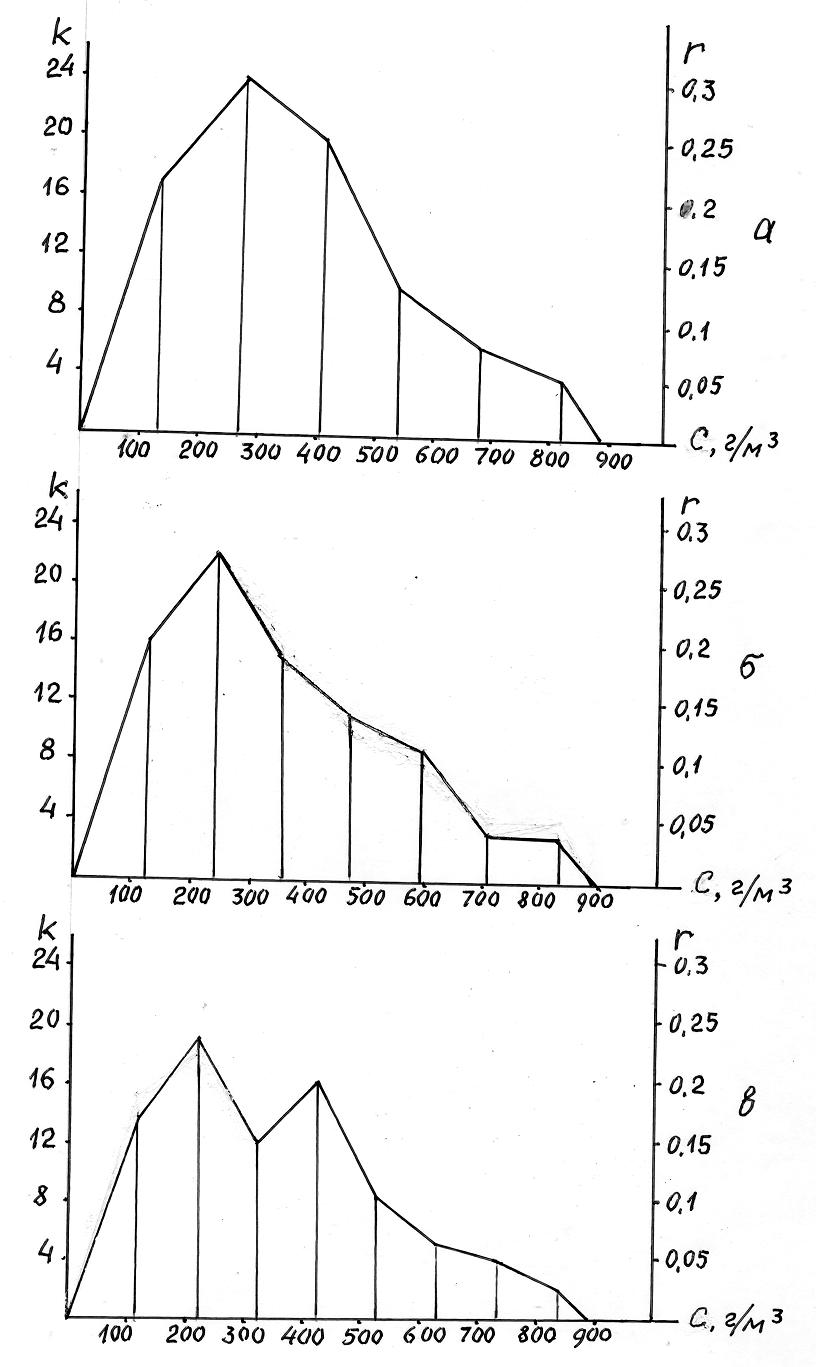
Рис. 1.4. Полигон распределения

а – табл. 1.3; б – табл. 1.4; в – табл. 1.5

1.4.3. Кумулята

Кумулята (кумулятивная кривая) строится в осях х признака и накопленных частот К и (или) накопленных частостей R.

Для построения кумуляты интервальные вариационные ряды, представляемые по форме табл. 1.3, 1.4 и 1.5, преобразуют в несколько иную форму (см. табл. 1.9, 1.10 и 1.11), в которой частоты и частости последовательно суммируют при переходе от одного интервала к другому. Последнему по старшинству интервалу в этом случае будет соответствовать накопленная частота, равная объему совокупности, а накопленная частость – равна единице. При этом на графике кумуляты для нижней границы первого интервала записывают значения частоты и частости, равные нулю.

Таблица 1.9

Характеристика интервального ряда (К = 6 классов)

№№ интервалов	Интервал содержания в классе, С (г/м3)	Cреднее значение содержания в интервале, С (г/м3)	Количество элементов в интервале (частота), k	Накопленная частота К	Относительная частота (частость), r	Накопленная частость R
1	64 – 201	132	17	17	0,21	0,21
2	202 – 338	269	24	41	0,30	0,51
3	339 – 475	406	20	61	0,25	0,76
4	476 – 612	543	9	70	0,11	0,87
5	613 – 749	680	6	76	0,08	0,95
6	750 – 886	817	4	80	0,05	1,00
			80		1,00

Таблица 1.10

Характеристика интервального ряда (К = 7 классов)

№№ интервалов	Интервал содержания в классе, С (г/м3)	Cреднее значение содержания в интервале, С (г/м3)	Количество элементов в интервале (частота), k	Накопленная частота К	Относительная частота (частость), r	Накопленная частость R
1	64 – 181	122	16	16	0,20	0,20
2	182 – 298	239	22	38	0,28	0,48
3	299 – 415	356	15	53	0,19	0,67
4	416 – 532	473	11	64	0,14	0,81
5	533 – 649	590	8	72	0,10	0,91
6	650 – 766	707	4	76	0,05	0,96
7	767 – 883	824	4	80	0,05	1,01
			80		1,01

Таблица 1.11

Характеристика интервального ряда (К = 8 классов)

№№ интервалов	Интервал содержания в классе, С (г/м3)	Cреднее значение содержания в интервале, С (г/м3)	Количество элементов в интервале (частота), k	Накопленная частота К	Относительная частота (частость), r	Накопленная частость R
1	64 – 167	116	14	14	0,18	0,18
2	168 – 270	219	19	33	0,24	0,42
3	271 – 373	322	12	45	0,15	0,57
4	374 – 476	425	16	61	0,20	0,77
5	477 – 579	528	8	69	0,10	0,87
6	580 – 682	631	5	74	0,06	0,93
7	683 – 785	734	4	78	0,05	0,98
8	786 - 888	837	2	80	0,02	1,00
			80		1,00

На рис. 1.5 представлены примеры построения кумулят для данных табл. 1.9, 1.10 и 1.11.

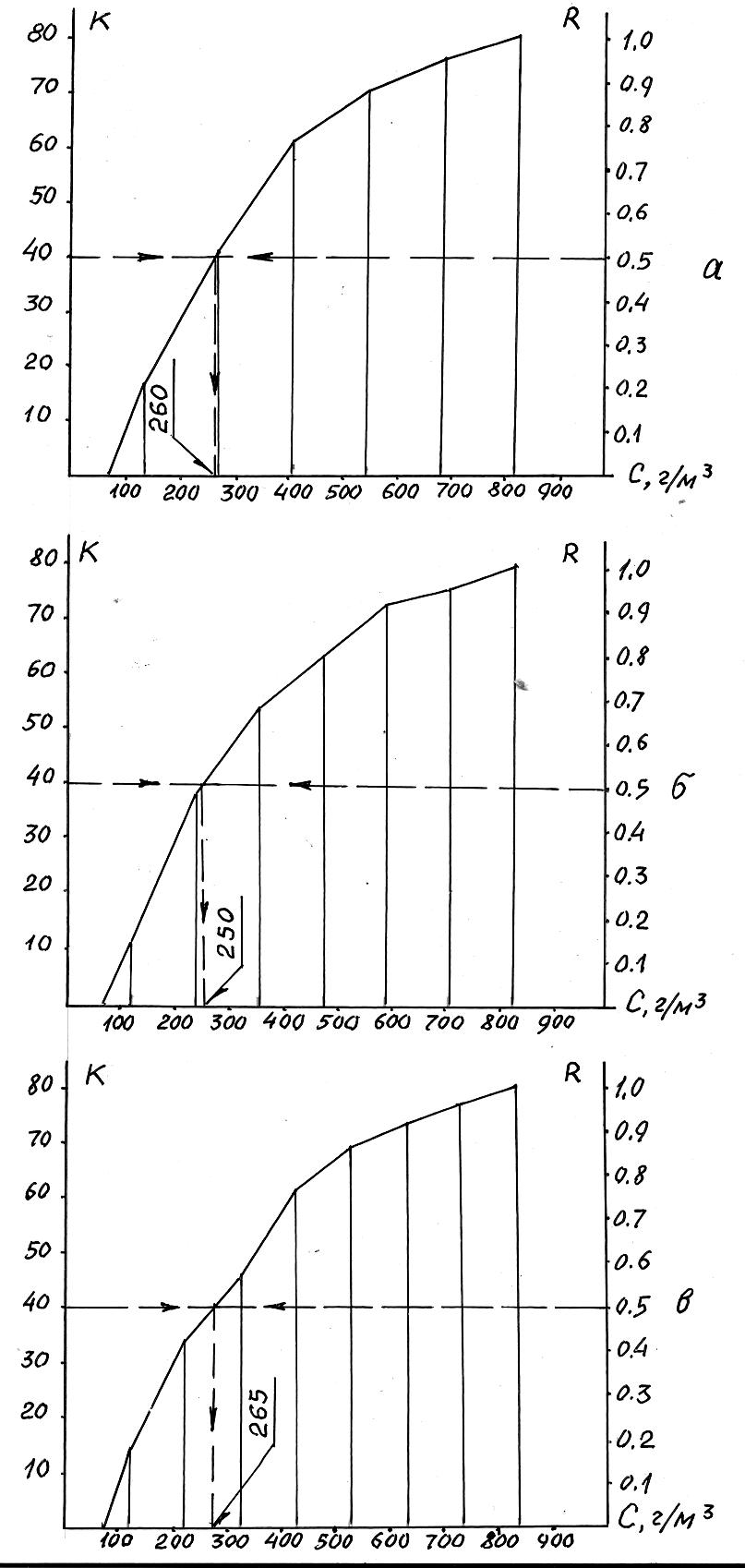
Рис. 1.5. Кумулята

а – табл. 1.3; б – табл. 1.4; в – табл. 1.5

Ранее (см. п. 1.3.4), был приведен пример определения медианы Ме с помощью упорядоченного вариационного ряда. То же самое, но графически, можно определить и с помощью кумуляты. Для этого необходимо провести по уровню R = 0,50 линию, параллельную оси х, до пересечения с кумулятой, а затем снести точку пересечения на ось х. Полученное значение и будет соотвествовать медиане. Так, по кумулятам рис. 1.5 а, б и в соответственно находим: Ме_(а) = 260 г/м³, Ме_(б) = 250 г/м³, Ме_(в) = 265 г/м³.

Напомним, что по упорядоченному вариационному ряду значение медианы Ме = 317,5 г/м³. Использовать упорядоченный вариационный ряд для нахождения медианы можно только для приблизительной ее оценки. При уточнении значения медианы лучше воспользоваться графиком кумуляты.